19.Наивероятнейшее число появления событий в последовательности независимых испытаний

Опр.: Наивероятнейшим числом m₀ наступления соб. А в n независим. испытаниях назыв. число, для кот. вер. превышает или по крайней мере не менее вер. каждого из остальных возм. исходов исп. Пусть соб. А наступило m₀ раз в n испы. Вер. появл. соб. А обозначим p; P(A)=p, а , тогда по формуле Бернули . По определению: -формула (1); -формула (2). Из нер-ва (1) получаем: ; ; . Т.к. q+p=1, то . Из нер-ва (2) получаем: ; ; ; . Т,о. для нахождения наивероятнейшего числа мы получили нер-во: . Замечание 1: Длина интервала, определяемая нер-вом равна 1; Замечание 2: Если границы интервала – дробные числа, то значение наивероятнейшего числа одно. Если границы – целые числа, то знач. наивер. числа два.

20.Формула Пуассона

Если вер. события p в отд. испытании близка к 0, то даже при большом числе испытаний n, но небольшой величине вероятности , получен. по лок. формуле Лапласа недостаточно близки к их ист. знач.м. В таких случаях применяют формулу Пуассона. Теорема: Если вер. p наступления соб. А в кажд. исп постоянна, но близка к 0, число независим. Исп. n достаточн. велико, а , то вер. того, что в n независ. испытаниях соб. А наступит m раз . Это формула Пуассона. Док-во: Для вычисления вер. воспользуемся ф. Бернулли:

(Т.к.,то)= Т.к. по условию n велико, то найдем предел правой части последн. равенства при , при этом будет получено приближен. значение вер.: = == = Пределы всех скобок, кроме предпоследн. равны 1 при . Сл-но вер. того, что в n исп. соб. появится m раз . Замечание: Ф. Пуассона обычно используют, когда , а .

21.Функция Лапласа.

Интегральная функция Лапласа.

Их применение для решения задач.

Исп-ть ф. Бернулли при достаточно большом кол-ве исп. затруднительно. Поэтому, когда используют т. Лапласа. Локальная т. Лапласа: Если вер. появления соб. А в каждом исп. постоянна и отлична от 0 и 1, то того, что соб. А появится в n испытаниях ровно m раз, ≈ равна (тем точнее, чем больше n) значению ф-ции: ,где ,где . Имеются таблицы, в кот. помещены знач. ф-ции. , соответствующие полож. знач-ям аргумента x. Для отриц. знач-ий аргумента пользуются теми же таблицами, т.к. функц. четная, т.е. . Вер. того, что соб. А появится в n испытаниях ровно m раз , где .

ИНТЕГР теор: Предположим, что производится n испытаний, в кажд. из кот. вер. появл. соб. А постоянна и равна p, . Нужно найти вер того, что соб. А появится в n испытаниях не менее k₁ и не более k₂ раз, т.е. нужно найти . Теорема.: Если вер. P наступления соб. в каждом исп. постоянна и отлична от 0 и 1, то вер. того, что в n испытаниях соб. А появится от k₁ до k₂ раз ,где (штрихи наоборот.) . При решении задач, требующих применения интегр. т. Лапласа, пользуются спец. таблицами. В них даны знач. ф-ции для полож. знач. аргумента x. Для x<0 функц. нечёт., т.е. . В табл. приведены знач. для . При x>5 значение ф-ции считается пост. и = 0,5. Для того, чтобы можно было исп-ть табл. функций Лапласа. преобразуем последнюю формулу: ; 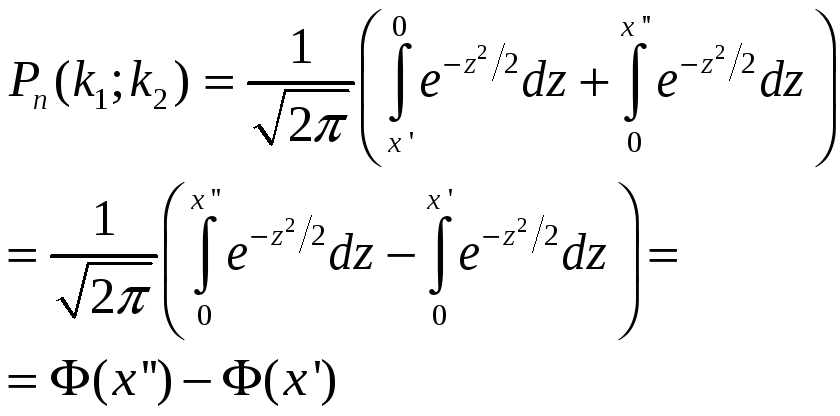, где . Вер. того, что соб. А появится в n независимых исп. от k₁ до k₂ раз равна .