44. Тригонометрические и обратно тригонометрические функции, их свойства и графики
Числовые функции, заданные формулами y=sinx, y=cosx, y=tgx, y=ctgx,называются тригонометрическими функциями. Каждая из них имеет соответственно свое название: синус, косинус, тангенс и котангенс.
Графики синуса и косинуса представляют собой синусоиду.
Свойства: D(y)=ℝ
Е(у)=[-1;1]
y=sinx-нечетная
y=cosx-четная
функции монотонны:
возрастающая:
y=sinx
на промежутке [-
+2πk;
+2πk]
y=cosx на промежутке [-π+2πk; 2πk]
убывающая: y=sinx
на промежутке [
;
y=cosx на промежутке [2πk; π+2πk]
периодические, Т=2πn
непрерывные
Графики функций y=tgx, y=ctgx представляют собой тангенсоиду.
Свойства:
D(y)
= (-
для y=tgx
D(y)
= (
E(y) = ℝ
функции нечетные
функции монотонны: y=tgx – возрастающая
y=ctgx – убывающая
периодические, Т=πn
непрерывные
45. Числовая последовательность, ограниченность, монотонность, предел последовательности, свойства
Опр: Последовательностью называется упорядоченные значения функции натурального аргумента f(n), взятые в порядке возрастания n.
Обозначение: (аn), {xn}, an, xn-n-ый член последовательности
Пример: 1;2;3;4;… хn=2n-1, {2n-1}, n€N
Опр: Последовательность {xn} называется ограниченной, если существует такое М>0, что для любого n>M, ⃓xn⃓<M
Опр: Последовательность называется возрастающей, если каждый ее член, начиная со второго больше предыдущего, т.е. хn+1>xn
Опр: Последовательность называется убывающей, если каждый ее член, начиная со второго, меньше предыдущего, т.е. хn+1<xn
Опр: Возрастающие и убывающие последовательности называются монотонными.
Опр:
Число а называется пределом
последовательности {xn},
если для любого сколь угодно малого
положительного числа
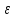найдется такое натуральное число N,
что при всех n>N
выполняется неравенство ( ⃓хn
- a⃓<
(
(
)
Замечание:
⃓хn
- a⃓<
xn
,
окрестность
т.хn
Тот факт, что а - есть предел последовательности {xn}геометрически означает, что в любой -окрестности т.а находятся все члены последовательности, начиная с некоторого номера, вне ее - конечное число членов последовательности.
Свойства:
Т1. Если последовательность имеет предел, то он единственный
Т2. Предел постоянной последовательности равен самой постоянной
Т3. Если последовательность имеет предел, то она ограниченна
Т4.(Теорема Вейерштрасса). Если последовательность монотонна и ограниченна, то она имеет предел.
Т5.(Об арифметических свойствах предела числовой последовательности)
Пусть
тогда
-
-
-
-
,
b
Пример:
