8.4.2 Робота в лабораторії

1. Запускаємо програму D_optimal і у відповідні вікна вписуємо значення згідно з варіантом, наприклад Х₁ = 50, Х₂ = 50, Х₁ =30, Х₂ =30, b₀=1, b₁=-3, b₂=2, b₁₁=3, b₁₂=4, b₂₂=-3,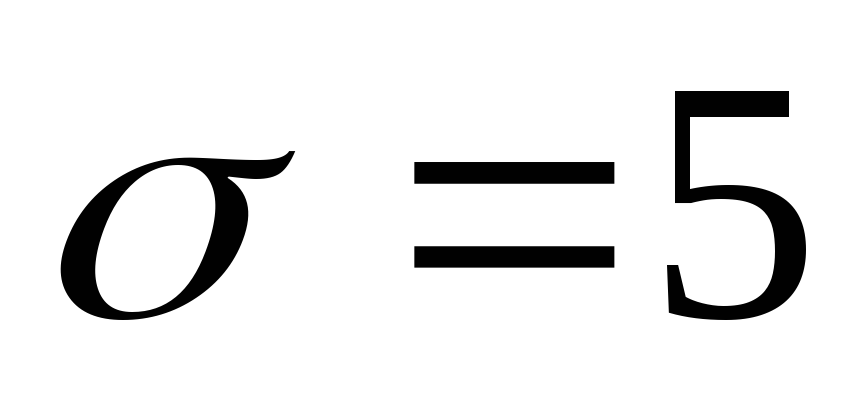, (рисунок 8.4) і натискаємо "далі".

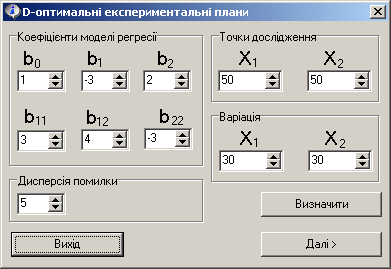
Рисунок 8.4 - Вікно програми D_optimal

2. Після натискання клавіші "далі" програма висвічує "вікно", в якому є пораховані значення з таблиці 8.1. Знайдені значення y і 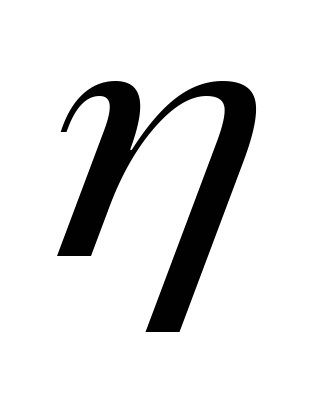виглядають так:

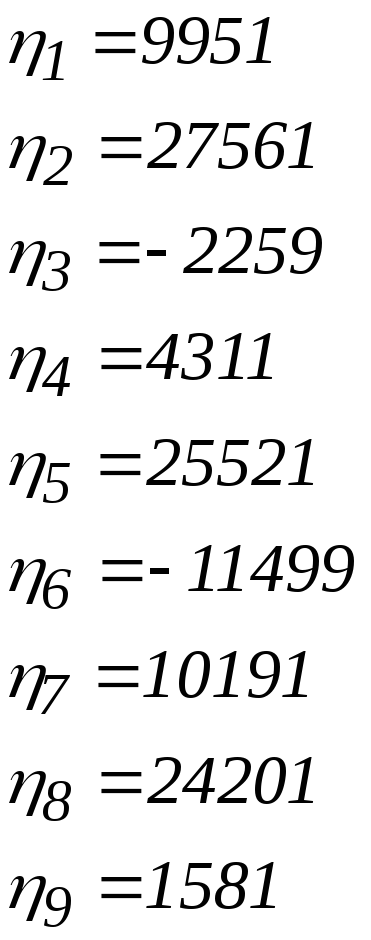
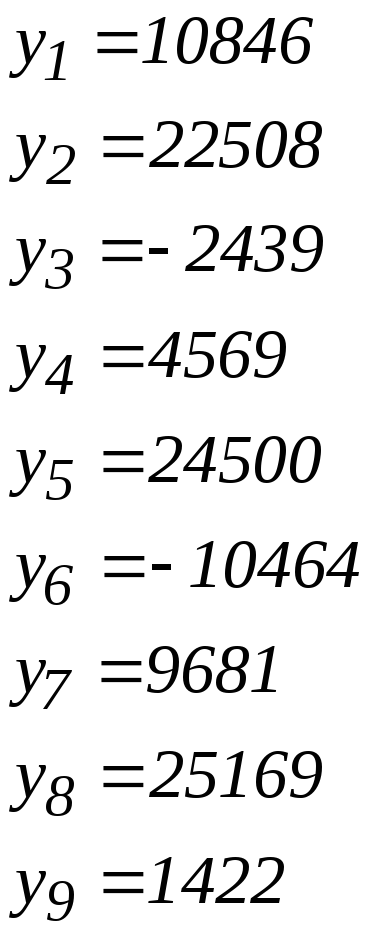
де _і – теоретичне значення функції,

y_і – експериментальне значення функції.

3. Отримані експериментальні і теоретичні значення функції підставляємо у формулу Бесселя і знаходимо :

При ймовірності Р=0,952 .

Знайдені значення підставляємо у формулу :

.

4. Знаходимо це або приблизне значення в таблиці 8.1. При цьому пам’ятаємо, що таких значень може бути декілька.

5. Шукане число знаходиться між 13-им і 14-им, 15-им і 16-им, 21-им і

22-им, 25-им і 26-им експериментами. Нам потрібно вибрати відповідно 14-ий, 16-ий, 22-ий, 26-ий експерименти.

6. Оскільки в нас декілька варіантів експериментів то перевіряємо умову

Для першого випадку коли =1,717 → ,

коли =1,762 → ,

коли =2,174 → ,

коли =2,277 → .

Умова виконується у всіх випадках, отже, можна зупинитися на 14-му експерименті.

7. Визначаємо коефіцієнтів. Для цього треба заповнити елементи матриці С. Вони знаходяться за формулами (8.26), (8.27), де і - елементи матриці F.

Знаходимо реальні значення у за формулою (8.24) підставляючи значення х, який приймає значення 20, 50, 80.

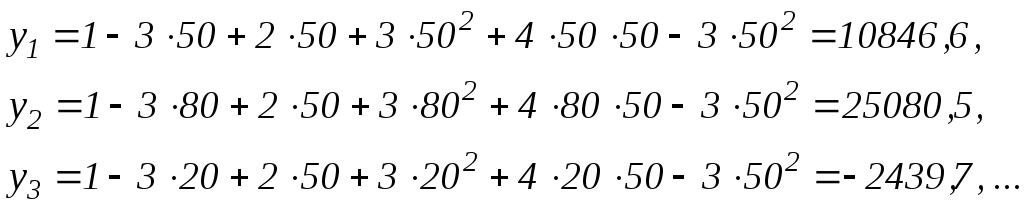
За цією ж формулою знаходимо у. Для цього замість значень аргументів х підставляємо значення -1, 0, 1, які відповідають 20, 50, 80 (це 5030).

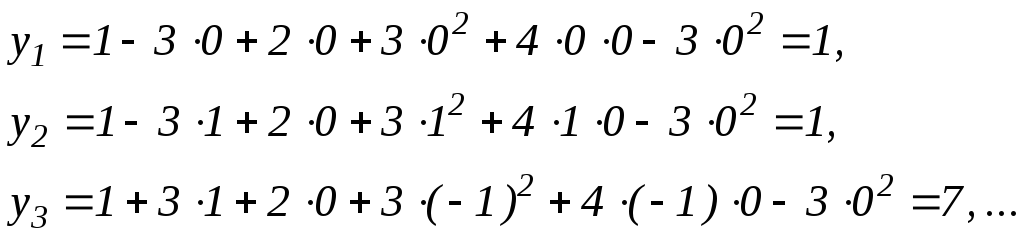
За допомогою програми знаходимо експериментальні значення у: ,

Після цього знаходимо експериментальні значення у за допомогою пропорції. Емпіричному у₁=1 відповідає дійсне у₁=9951. Записуємо пропорцію

1  10846,6

y₁  9951.

Знаходимо

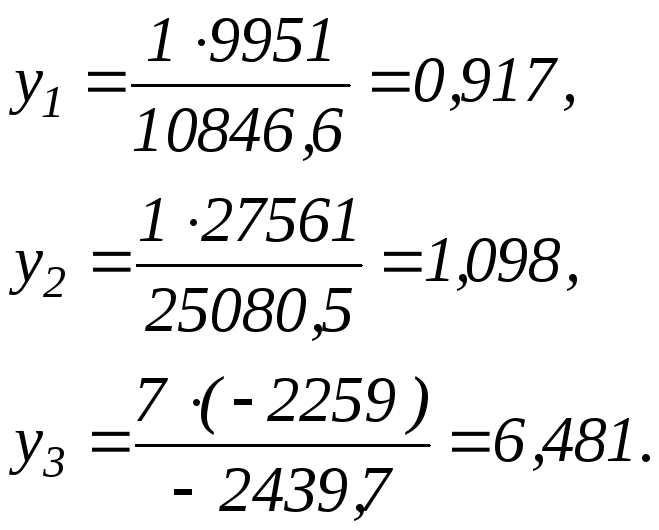
Ці значення у підставляємо у формулу (8.28) для знаходження .

α₁₁ = 0,917·1 + 1,098·1 + 6,481·1 + 0·1 + 4,166·1 + 2,197·1 – 4,21·1 – 7,692·1 + 6,666·1 –

– 7,692·1+4,166·1+6,666·1+2,197·1+0,917·1=15,877;

α₂₁ =0,917·0 + 1,098·1 – 6,481·1 + 0·0 + 4,166·1 – 2,197·1 – 4,21·0 – 7,692·1 – 6,666·1 – 7,692·1+ +4,166·1 – 6,666·1 – 2,197·1 + 0,917·0 = –30,161; …

С₁₁ = 1² + 1² + 1² + 1² + 1² + 1² + 1² + 1² + 1² + 1² + 1² + 1² + 1² + 1² = 14;

С₁₂ = С₂₁ = 0·1 + 1·1 – 1·1 + 0·1 + 1·1 – 1·1 + 0·1 + 1·1 – 1·1 + 1·1 + 1·1 – 1·1 – –1·1 + 1·0 = 0;

С₂₂ = 0² + 1² + (–1)² + 0² + 1² + (–1)² + 0² + 1² + (–1)² + 1² + 1² + (–1)² + (–1)² +

+ 0² = 10; …

Матриця С матиме вигляд:

,.

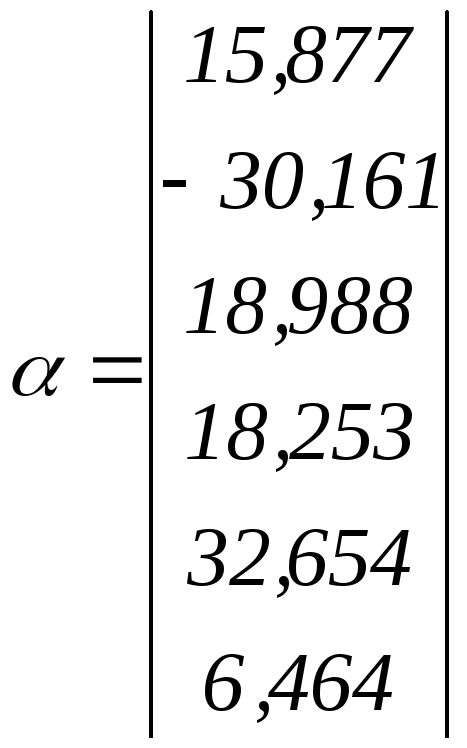З цих матриць складаємо систему рівнянь:

.

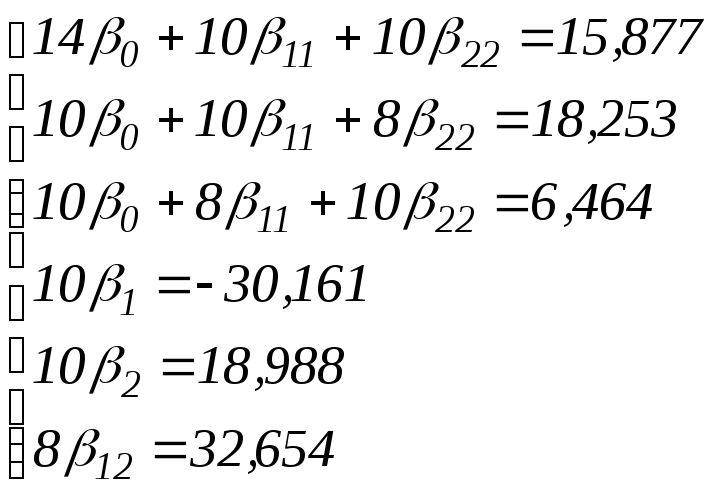Звідси: , , , , ,

.

Як бачимо: b₀=1, b₁=-3, b₂=2, b₁₁=3, b₁₂=4, b₂₂=-3. Тому:

Δ b₀= b₀ -β₀=1-0,742=0,258, γ₀= (Δ b₀ / b₀)·100%=0,258/1·100%=25,8%,

Δ b₁= b₁ - β₁ = -3+3,016=0,016, γ₁= (Δ b₁ / b₁)·100%=0,016/(-3)·100%=0,5%,

Δ b₂= b₂-β₂=2 - 1,899=0,101, γ₂= (Δ b₂ / b₂)·100%=0,101/2·100%=5%,

Δ b₁₁= b₁₁-β₁₁=3 - 3,221= - 0,221, γ₁₁= (Δ b₁₁ / b₁₁)·100%=-0,221/3·100%=7,3%,

Δ b₁₂= b₁₂-β₁₂=4 – 4,082= -0,082, γ₁₂= (Δ b₁₂ / b₁₂)·100%= -0,082/4·100%=2%,

Δ b₂₂= b₂₂-β₂₂=-3+2,673=-0,327, γ₂₂= (Δ b₂₂ / b₂₂)·100%= -0,327/(-3)·100%=10%.

Найбільша похибка отримана при розрахунку β₀.