
Модель стохастической процентной ставки
Определение: Вероятности P и Q называются эквивалентными, если существует стохастический процесс γ(w, t), что каждому А, принадлежащему G=2Ω
![]()
Теорема (Гирсанова): Вероятность P* является риск-нейтральной, если существует процесс γ(t), что каждому А, принадлежащему G, что
![]() ,
,
где
 ,
s
– время. Кроме того
,
s
– время. Кроме того
![]() - винеровский процесс относительно P*.
- винеровский процесс относительно P*.
Замечание: M(ω,t) называется стохастическим дисконтирующим фактором.
Теорема (о существовании риск-нейтральной вероятности процесса Ито):
Пусть
![]() (*)
(*)
- процесс Ито. Тогда существует риск-нейтральная вероятность P*, относительно которой решение дифференциального уравнения (*) есть
![]() ,
,
![]() -
винеровский процесс относительно P*.
-
винеровский процесс относительно P*.
Доказательство:
Воспользуемся
теоремой Гирсанова и найдем процесс
γ(t),
чтобы
![]() или
или
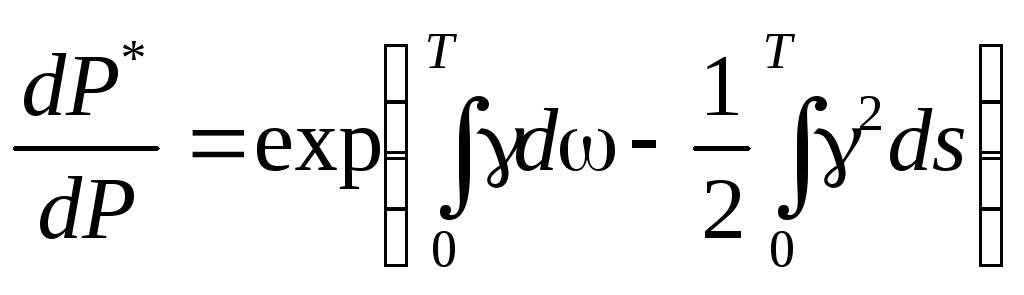 .
Тогда
.
Тогда
![]() ,
где
,
где
![]() - винеровский процесс относительно Р*,
а W
– винеровский процесс относительно Р.
- винеровский процесс относительно Р*,
а W
– винеровский процесс относительно Р.
Обозначая
![]() ,
имеем:
,
имеем:
![]()
- дифференцируем по стохастической части, которой нет в γt.
Исходное дифференциальное уравнение:
![]()
Выбирая
![]() -
цена риска
– показатель Шарпа, получаем:
-
цена риска
– показатель Шарпа, получаем:
![]()
Получили
новое дифференциальное уравнение
относительно риск-нейтральной вероятности
Р*,
так как в случае
![]() и
и
![]() определяет риск-нейтральную эволюцию
капитала:
определяет риск-нейтральную эволюцию
капитала:
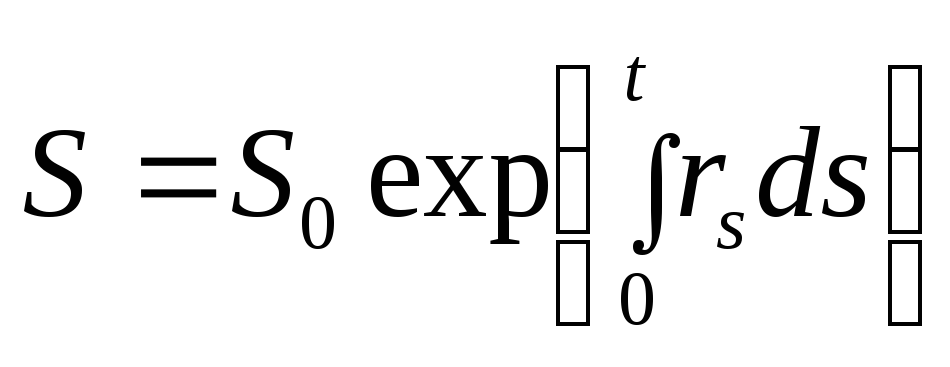 или капитал, получаемый инвестированием
в безрисковый актив под безрисковую
процентную ставку. Значит, нашли
или капитал, получаемый инвестированием
в безрисковый актив под безрисковую
процентную ставку. Значит, нашли
![]() ,
которая определяет Р*.
Найдем решение исходного ДУ
(*)
относительно
Р*.
,
которая определяет Р*.
Найдем решение исходного ДУ
(*)
относительно
Р*.
Известно общее решение относительно Р:
![]()
Так
как (*) преобразуются в уравнение
![]() ,
эквивалентное
исходному относительно риск-нейтральной
вероятности, то
,
эквивалентное
исходному относительно риск-нейтральной
вероятности, то
![]() или
расписывая
или
расписывая
d(ln S), получим:
![]() ,
,
чтд.
В доказанной теореме процентная ставка является постоянной. Перейдем к рассмотрению процентной ставки стохастического процесса. Пусть r = r(W,t).
Определение: Пусть P(t,T) – цена бескупонной облигации в момент t<T, t – время погашения. Мгновенной форвардной процентной ставкой назовем функцию
![]() или,
что то же самое,
или,
что то же самое,
 ,
T
= const
,
T
= const
Определение: Безрисковой процентной ставкой назовем r(t) = rt = f(t,t).
Замечание:
Если
Вt
– цена облигации в момент t,
В0
– её номинальная стоимость, то
![]() ,
откуда
,
откуда
 .
Если rs=r(s)=r
–
постоянная ставка, то
.
Если rs=r(s)=r
–
постоянная ставка, то
![]() - непрерывно начисляемый процент.
- непрерывно начисляемый процент.
Пусть
форвардная процентная ставка является
процессом Ито, т.е представима в виде
![]() .
Интегрируя,
.
Интегрируя,
![]()
Так
как rt
=
f(t,t),
то
![]() .
Следовательно, так
.
Следовательно, так
как
 ,
то
,
то
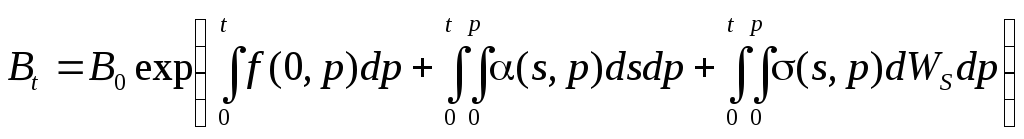 .
.
Меняя пределы интегрирования по теореме Фубини, получим:
 . (1)
. (1)
Кроме
того, так как
 ,
подставляя выражение
f(t,Т)
и
применяя теорему Фубини, аналогично
получаем:
,
подставляя выражение
f(t,Т)
и
применяя теорему Фубини, аналогично
получаем:
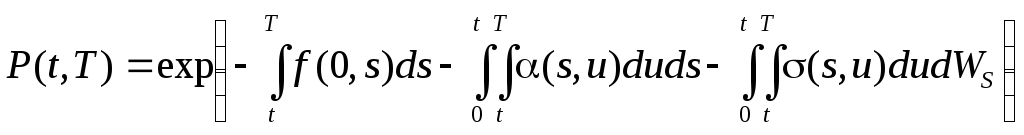 . (2)
. (2)
Обозначим для простоты написания:
![]()
Теорема 2 (без доказательства): Если уравнение
![]() (3)
(3)
имеет единственное решение γt, то существует риск – нейтральная вероятность Р* для дисконтированной цены
![]()
Кроме того, замена переменного вида
![]() (4)
(4)
не меняет вероятность Р*.
Используем
теорему 2. Пусть
![]() - винеровский процесс относительно риск
– нейтральной вероятности Р*.
Тогда, так как
- винеровский процесс относительно риск
– нейтральной вероятности Р*.
Тогда, так как
![]() ,
,
пользуясь заменой (4) имеем:
![]() ,
,
или дифференцируя по t, имеем:
![]()
Определим цену P(t,T) относительно риск – нейтральной вероятности Р*.
Рассмотрим![]()
![]() (воспользуемся
свойством интегралов
(воспользуемся
свойством интегралов
![]() для
для
![]() и
и
![]() )
=
)
=
![]() .
.
Полагая в (1) начальный капитал В0=1, видим, что последние три слагаемые и есть ln Bt. Тогда
![]() (5)
(5)
В
то время,
 ,
то есть
,
то есть
![]() при
условии
при
условии
![]() .
Вдобавок, мы видим из (5):
.
Вдобавок, мы видим из (5):
![]() .
.
Допустим,
что из уравнения (3) мы нашли γt.
Перейдем от текущей вероятности Р
к Р*:![]() .
.
Тогда в (5) имеем:

(пользуясь
(3)) =![]() . (6)
. (6)
Ранее мы получили, что относительно риск – нейтральной вероятности
![]() ,
,
или, меняя Т на t, имеем
![]() .
.
Так как rt=f(t,t), то из последнего
![]() .
(7)
.
(7)
Интегрируя обе части уравнения (6) по промежутку [0,t], имеем:
![]()
Подставим последнее равенство в (6):
![]() -
искомая цена Р(t,T)
относительно риск – нейтральной
вероятности.
-
искомая цена Р(t,T)
относительно риск – нейтральной
вероятности.
Кроме
того, из (6)
 .
.
Дифференцируя его по формуле Ито получим:
![]()
– дифференциальное уравнение для цены бескупонной облигации в момент времени t.
