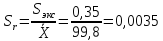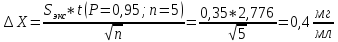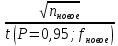ДЗ 3 аналит

Московский технологический университет

Институт тонких химических технологий

Кафедра аналитической химии имени И.П.Алимарина

Домашнее задание №3

Статистическая обработка результатов анализа

Группа ХББО-01-16

Студентка Иванова Е.А

Преподаватель: Романовская Л.Е.

Москва 2017

Вариант 9

ДАНО:

Первая серия: Вторая серия:

X₁ = 101,1 мг/мл 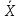(P=0,95; n = 5) = 99,8 мг/мл

X₂ = 101,5 мг/мл S = 0,35 мг/мл

X₃ = 101,0 мг/мл X_{действ .}= 100,2 мг/мл

X_{действ .}= 100,2 мг/мл

S_r = 0,0010

РЕШЕНИЕ:

Задание 1: Провести статистическую обработку результатов анализа каждой серии. Привести полную запись результатов анализа. Оценить величину случайной и систематической погрешности.

1. Обработка первой серии:

1. Проверим выборку на грубые промахи по Q-критерию:

А) По Q-критерию можно проверять лишь крайние значения, поэтому расположим выборку по возрастанию :

101,0 101,1 101,5

Б) Рассчитаем экспериментальные значения критерия:

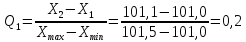
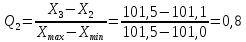
В) Сравним с табличным значением и сделаем вывод о наличие грубых промахов в выборке:

Q_табл=0,970 (Р=0,95 ; n= 3)

Q₁ ˂ Q_табл (0,2 ˂ 0,970) – X₁ НЕ ЯВЛЯЕТСЯ грубым промахом

Q₃ ˂ Q_табл (0,8 ˂ 0,970) – X₃ НЕ ЯВЛЯЕТСЯ грубым промахом

2. Найдем среднее значение:

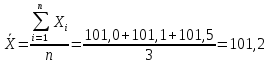мг/мл

3. Рассчитаем стандартное отклонение и относительное стандартное отклонение:

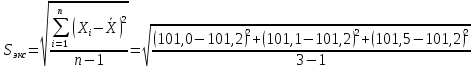= 0,27 мг/мл

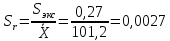
4. Поскольку S_r методики задано, следует проверить по χ² -критерию достигнута ли требуемая воспроизводимость:

А) Рассчитаем S_ожид:

S_ожид=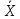 *S_{r методики} = 101,2 * 0,0010 = 0,1012 мг/мл

Б) Рассчитаем экспериментальное значение критерия:

В) Сравним с табличным значением критерия и сделаем вывод о достижимости требуемой воспроизводимости:

χ² = 5,991 (P= 0,95; f = n-1 = 2)

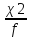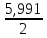= = 2,996

(2,996 < 7,118)

Поскольку табличное значение критерия меньше, чем рассчитанное для выборки и S_r методики, то требуемая воспроизводимость НЕ ДОСТИГНУТА.

5. Рассчитаем доверительный интервал: поскольку требуемая воспроизводимость не достигнута, то рассчитаем доверительный интервал по следующей формуле:

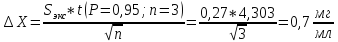
6. Полная запись результатов:

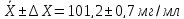(P=0,95; n=3)

7. Рассчитаем абсолютную случайную погрешность:

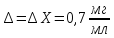
8. Рассчитаем относительную случайную погрешность:

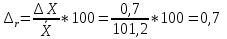
9. Оценим правильность анализа и величину систематической погрешности:

А) Рассчитаем экспериментальное значение коэффициента Стьюдента:

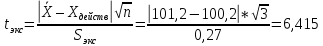
Б) Сравним с табличным значением критерия и сделаем вывод о наличии правильности в анализе:

t_табл (P = 0,95; f = n – 1 = 2) = 4,303

t_табл < t_эксп (4,303 < 6,415) – выявлена систематическая погрешность. Анализ выполнен НЕВЕРНО.

в) Оценим величину систематической погрешности:

Абсолютная систематическая погрешность:

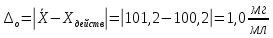
Относительная систематическая погрешность:

2. Обработка второй серии

Поскольку для второй серии задано среднее значение и стандартное отклонение, то нам следует рассчитать только относительное стандартное отклонение и доверительный интервал

1. 

2. 

3. 

(P=0,95; n=5)

4. Рассчитаем абсолютную случайную погрешность:

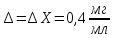
5. Рассчитаем относительную случайную погрешность:

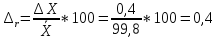
6. Оценим правильность анализа и величину систематической погрешности:

А) Рассчитаем экспериментальное значение коэффициента Стьюдента:

Б) Сравним с табличным значением критерия и сделаем вывод о наличии правильности в анализе:

t_табл (P = 0,95; f = n – 1 = 4) = 2,776

t_табл > t_эксп (2,776 < 2,556) – систематическая погрешность на фоне случайной не выявлена. Анализ выполнен ВЕРНО.

в) Оценим величину систематической погрешности:

Абсолютная систематическая погрешность:

Относительная систематическая погрешность:

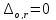
Задание 2: Значимо ли расхождение между результатами определений двух серий? Рассчитайте доверительный интервал при объединении двух серий? Рассчитайте доверительный интервал при объединении двух серий определений и приведите полную запись результатов.

Для того чтобы выяснить значимо ли расхождение между результатами определений двух серий следует использовать критерий Фишера (F–критерий), для проверки однородности дисперсий и t–критерий (значение коэффициента Стьюдента) для проверки принадлежности средних одной генеральной совокупности.

1) Проверка однородности дисперсий по критерию Фишера:

А) Рассчитаем экспериментальное значение критерия Фишера (S2 ˃ S1):

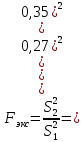
Б) Сравним с табличным значением критерия и сделаем вывод об однородности дисперсий:

F_табл (P = 0,95; f₁= n – 1 = 2; f₂= n – 1 = 4) = 6,944

F_табл ˃ F_эксп (6,388 ˃ 1,34) – стандартные отклонения принадлежат одной выборке.

2) Проверка принадлежности средних значений одной генеральной совокупности, используя экспериментальное значение коэффициента Стьюдента:

А) Рассчитаем средневзвешенное стандартное отклонение:

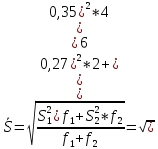
б. Рассчитаем экспериментальное значение коэффициента Стьюдента:

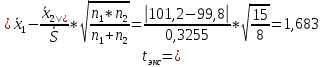
В) Сравним с табличным значением критерия и сделаем вывод о принадлежности средних значений одной генеральной совокупности:

t_табл (P = 0,95; f = n₁+n₂–2 = 6) = 2,447

t_табл > t_экс – средние значение ПРИНАДЛЕЖАТ одной выборке. Объединение выборки возможно.

3) Рассчитаем среднее значение:

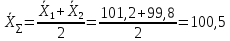мг/мл

4) Рассчитаем доверительный интервал:

5) Полная запись:

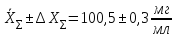
Задание №3: Каково должно быть число параллельных определений, чтобы погрешность анализа уменьшилась вдвое? (на примере одной из серий определений).

Расчеты проведем на примере второй выборки:

1. 

2. 

3. 

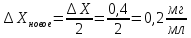
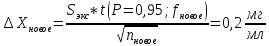
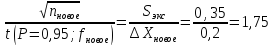
4. Составим таблицу и подбираем значение n_новое и t (P = 0,95; f_новое) таким образом, чтобы соотношение было больше или равно 1,75:

nновое	t (P=0,95; fновое=nновое-1)
6	2,571	0,95
7	2,447	1,08
8	2,365	1,20
9	2,306	1,30
10	2,262	1,40
11	2,228	1,49
12	2,201	1,57
13	2,179	1,65
14	2,160	1,73
15	2,145	1,81

Вывод: чтобы погрешность второй серии анализов уменьшилась вдвое, необходимо провести минимум 15 параллельных определений.