3 Расчет датчика обратной связи

Принцип действия индукционных расходомеров основан на измерении пропорциональной расходу электродвижущей силы, индуктированной в потоке электропроводной жидкости под действием внешнего магнитного поля.

Величина этой э.д.с. для расходомеров, где магнитное поле изменяется во времени с частотой fопределяется по формуле:

, (9)

где E– э.д.с.,

В – магнитная индукция в зазоре между полюсами магнита,

υ – скорость течения жидкости,

d– внутренний диаметр трубопровода,

f– частота промышленного тока.

Выражая скорость υ через объемный расход Q, получим:

, (10)

где Q– объемный расход жидкости,

d– внутренний диаметр трубопровода,

f– частота промышленного тока.

Для данной системы приняты следующие характеристики:

B=300 мТл,

d=2.5∙10^-2см,

f=50 Гц.

Таким образом, получаем уравнение для определения вида статической характеристики датчика:

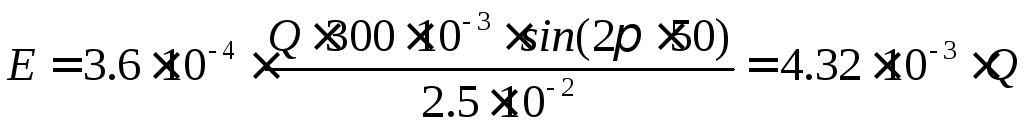
По уравнению видно, что данная характеристика линейная и при максимальном расходе воды в рассматриваемой системе возникающая при этом э.д.с не будет превышать 10^-5 В, что свидетельствует о том, что данное устройство не влияет на работу других электромагнитных устройств в разрабатываемой системе всилу малой э.д.с, наводимой в данном датчике расхода жидкости. поэтому следует сделать вывод, что данный датчик расхода жидкости подходит как по техническим параметрам разрабатываемой системы, так и по электрическим параметрам, создавая в ходе работы столь малые магнитные поля помех, что никак не отразится на устройствах, работающих также в разрабатываемой системе.

E, 10^-6В

0.27

12

0

Q, 10^-3м³/с

Рисунок 4 – Статическая характеристика датчика расхода жидкости

4 РАСЧЕТ ПЕРЕДАТОЧНОЙ ФУНКЦИИ СИСТЕМЫ, АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМЫ

4.1 Расчет передаточной функции САУ процессом полива газона

На рисунке 1 отображена структурная схема системы автоматического управления поливом газона. Найдем передаточную функция системы в общем виде путем преобразования структурной схемы:

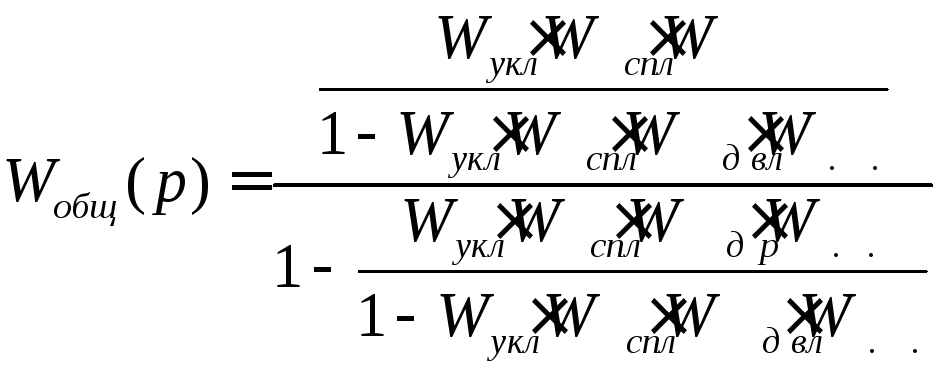. (11)

Подставив полученные ранее передаточные функции всех элементов системы и упростив выражение с помощью программы MathCadполучим передаточную функцию разомкнутой САУ процессом полива газона:

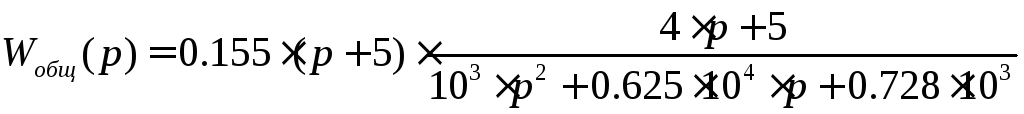. (12)

Воспользовавшись программой MathCadнайдем функцию переходного процесса и построим его график:

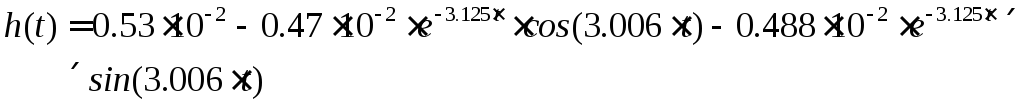
По графику переходного процесса (рисунок 5) определим прямые оценки качества системы.

h_уст=120 – установившееся состояние переходного процесса,

h_max=132,5 – максимальное значение переходного процесса,

t_р=12,25с – время регулирования.

Перерегулирование ,

что вполне удовлетворяет техническому заданию, так как при разработке данной системы допускается 5% несовпадение заданного значения перерегулирования (10%) и полученного в ходе анализа графика переходного процесса.

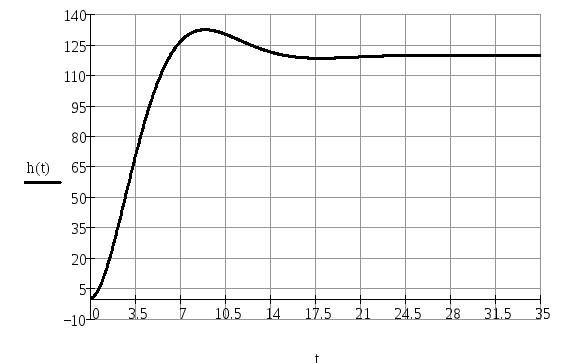
Рисунок 5 – Переходный процесс САУ процессом полива газона

Построим амплитудно-частотную характеристику для того, чтобы определить косвенные оценки качества системы. Для того, чтобы определить амплитудно-частотную характеристику системы, необходимо в передаточной функции рзаменить наjw. Затем знаменатель уравнения помножить на сопряженное выражение, а потом выделить действительную и мнимую части из полученного выражения по формулам определить амплитудно-частотную характеристику, то есть:

(13)

Построим амплитудно-частотную характеристику (рисунок 6), используя прикладную программу MathCad, и по графику амплитудно-частотной характеристики САУ процессом полива газона определим косвенные оценки качества САУ процессом полива газона.

Косвенные оценки качества САУ процессом полива газона.

А_max=0,0053 – максимальная амплитуда сигнала.

w₁=0 Гц,w₂=0,12 Гц – полоса пропускания.

w, Гц

A(w)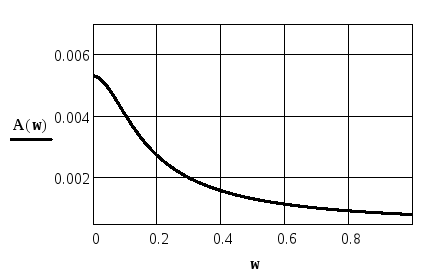

Рисунок 6 – Амплитудо-частотная характеристика САУ процессом полива газона

4.2 Определение устойчивости по критерию Гурвица

Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительными.

По коэффициентам характеристического уравнения:

, (14)

составляется определитель Гурвица.

Для этого по главной диагонали определителя выписываются все коэффициенты характеристического уравнения, начиная со второго, затем вверх записываются коэффициенты с возрастающим индексом, а вниз с убывающим индексом.

Составленный определитель называется главным определителем Гурвица, он имеет порядок, совпадающий с порядком характеристического уравнения. Из главного определителя составляются частные определители первого, второго, третьего и так далее порядков их образования из главного определителя.

Вычисляя главный определитель и частные определители, Гурвиц установил, для того, чтобы система была устойчива необходимо и достаточно, чтобы все определители были положительны.

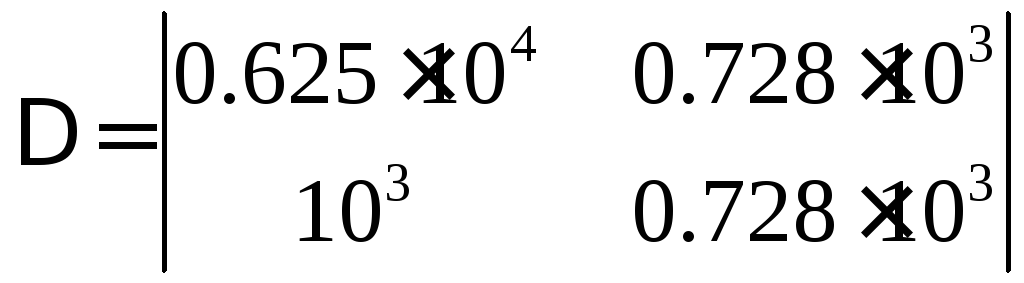(15)

Вычислим миноры в определителе Гурвица:

Все миноры определителя Гурвица больше ноля, следовательно система устойчива.

4.3 Проведение z-преобразования передаточной функции САУ процессом полива газона с дискретным элементом

Z-преобразование проведем по формуле:

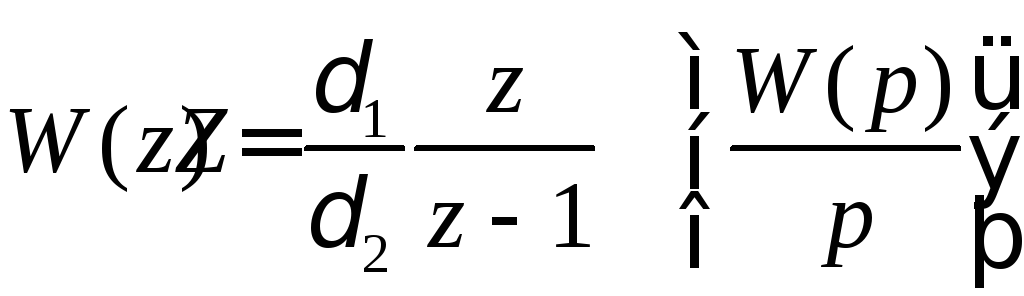, (16)

где и- показатели цифрового преобразования. В рамках курсовой работы принимает их равными 1;

- передаточная функция импульсной системы.

. (17)

Воспользовавшись программным продуктом MathLabможно получить передаточную функцию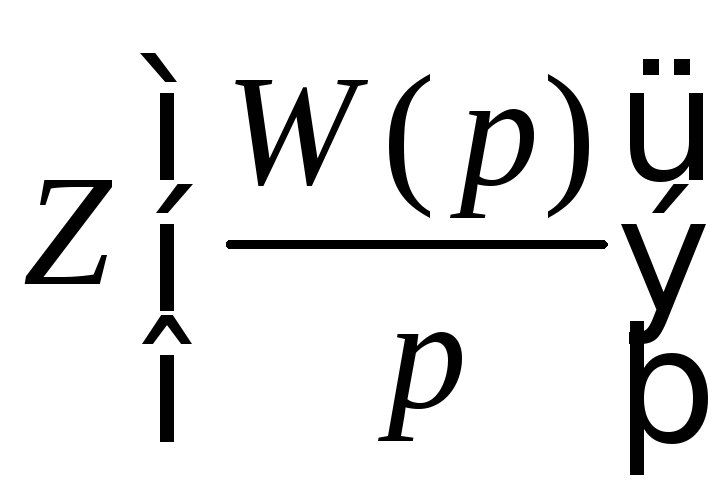по приведенной ниже программе:

>> W=tf([0.62 3.875 3.875],[1000 6250 728 0])

Transfer function:

0.62 s^2 + 3.875s+ 3.875

---------------------------

1000 s^3 + 6250 s^2 + 728 s

>> W=c2d(W,1.5)

Transfer function:

0.00141 z^2 - 0.0001203 z + 1.268e-005

--------------------------------------

z^3 - 1.837 z^2 + 0.837 z - 8.482e-005

Sampling time: 1.5

Таким образом итоговое z-преобразование будет выглядеть следующим образом:

.

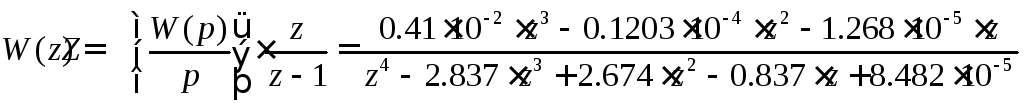Определим устойчивость полученной импульсной системы по критерию Шур-Кона. Для устойчивости импульсной системы необходимо, чтобы коэффициенты характеристического уравнения были положительны:

В нашем случае характеристическое уравнение:

. (18)

В характеристическом уравнении есть отрицательный коэффициент, следовательно, импульсная система не устойчива.

Проверим условия:

Составим определители Шур-Кона.

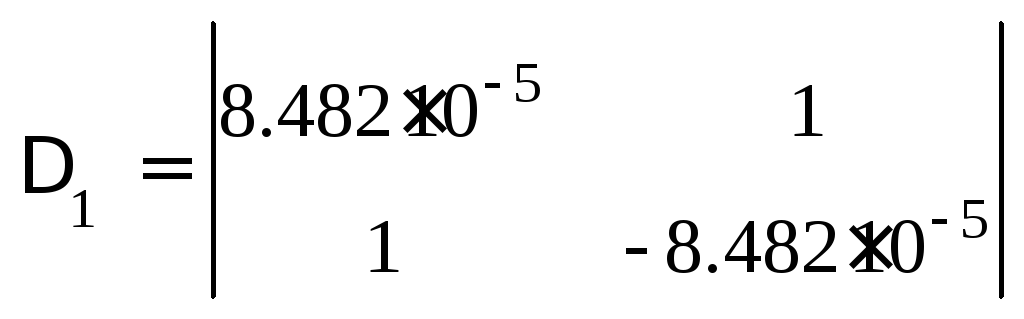
Посчитаем нечетные миноры матрицы. Для того, что бы система была устойчивой, чтобы нечетные миноры матрицы Шур Кона были меньше нуля, либо четные миноры матрицы были больше нуля.

Посчитав миноры в MathCAD, получили:,,,.

Таким образом, по критерию Шур-Кона получаем, что данная дискретная система устойчива.

Построим переходный процесс цифровой системы.

t, c

h(t)

Рисунок 7 – Переходный процесс дискретной САУ процессом полива газона

По данному рисунку видно, что переходный процесс сходящийся, что в некоторой степени свидетельствует о том, что дискретная система также является устойчивой, и нет необходимости в коррекции рассматриваемой дискретной CАУ процессом полива газона.