
- •Преобразование Лапласа
- •Нахождение изображений
- •Теоремы подобия, смещения, запаздывания
- •Поиск изображения по графику оригинала
- •Отыскание оригинала по изображению
- •Дифференцирование оригиналов и изображений
- •Интегрирование оригиналов и изображений
- •Свертка функций
- •Решение дифференциальных уравнений
- •Решение систем дифференциальных уравнений
- •Решение интегральных уравнений
Решение дифференциальных уравнений
Если дано линейное дифференциальное уравнение порядка n с постоян-ными коэффициентами
y(n)
+ a1y(n
– 1) +
. . . + a0y
=
![]() (t)
( 15 )
(t)
( 15 )
где
![]() (t)
является оригиналом
(t)
является оригиналом
![]() (t)
=: Ф(p)
и заданы начальные условия вида y(0)
= y0
, y`(0)
= y1
, y``(0)
= y2
, . . . , y(n
– 1)(0)
= yn
– 1 ( задача
Коши ), то решение уравнения y(t)
так же полагаем оригиналом и y(t)
=: F(p).
Перейдем в ( 15 ) по формулам ( 7 ), ( 8 ), (
9 ) к изображению производных и получим
линейное уравнение относительно F(p)
(изображающее
уравнение). Решим
это уравнения и по изображению определим
оригинал y(t)
=: F(p)
, который и
является решением задачи Коши.
(t)
=: Ф(p)
и заданы начальные условия вида y(0)
= y0
, y`(0)
= y1
, y``(0)
= y2
, . . . , y(n
– 1)(0)
= yn
– 1 ( задача
Коши ), то решение уравнения y(t)
так же полагаем оригиналом и y(t)
=: F(p).
Перейдем в ( 15 ) по формулам ( 7 ), ( 8 ), (
9 ) к изображению производных и получим
линейное уравнение относительно F(p)
(изображающее
уравнение). Решим
это уравнения и по изображению определим
оригинал y(t)
=: F(p)
, который и
является решением задачи Коши.
В
случае ЛДУ второго порядка y``
+ a
y`
+ by
=
![]() (t)
( 16 )
(t)
( 16 )
имеем
y(0)
= y0
, y`(0)
= y`0,
y(t)
=: F(p),
![]() (t)
=: Ф(p).
По формулам ( 6 ), ( 7 ) имеем y`(t)
=: p
F(p)
- y0
, y
``(t)
=: p2
F(p)
– p
y0
– y`0
и
приходим
к изобра- жающему уравнению
(t)
=: Ф(p).
По формулам ( 6 ), ( 7 ) имеем y`(t)
=: p
F(p)
- y0
, y
``(t)
=: p2
F(p)
– p
y0
– y`0
и
приходим
к изобра- жающему уравнению
p2 F(p) – p y0 – y`0 + a[ p F(p) - y0 ] + b F(p) = Ф(p)
F(p) [ p2 + ap + b ] = Ф(p) + y`0 + (p + a) y0
Решение
для изображения: F(p)
=
![]() ( 17 )
( 17 )
Пр.18 Решить ЛДУ y``+ 6y`+ 9y = 9e3t при условии y(0) = y`(0) = 0.
Решение
1. Пусть
y(t)
=: F(p),
тогда y`(t)
=: p
F(p),
y
``(t)
=: p2
F(p),
9e3t
=![]() (№3) и приходим к изображающему уравнению
(№3) и приходим к изображающему уравнению
p2
F(p)
+ 6p
F(p)
+ 9 F(p)
=
![]() или F(p)(p2
+ 6p
+ 9) =
или F(p)(p2
+ 6p
+ 9) =
![]() .
Решение представим в виде суммы
простейших дробей
.
Решение представим в виде суммы
простейших дробей
F(p)
=
![]() =
=
![]() +
+
![]() +
+
![]() и просуммируем их.
и просуммируем их.
Числитель A(p + 3)2 + B(p2 – 32) + C(p – 3) = 9 приводит к системе 3 уравнений
p2 | A + B = 0 A = ¼ Переход от изображения к оригиналу
p1
| 6A
+ C
= 0
![]() B
= - ¼ по формулам № 3, 8 дает
B
= - ¼ по формулам № 3, 8 дает
p0 | 9A – 9B – 3C = 9 C = - 3/2
y(t) = ¼ e3t - ¼ e - 3t - 3/2 t e-3t
Решение
2.
Пусть
y(t)
=: F(p)
и
9e3t
=:
Ф(p).
Решение
изображающего уравнения F(p)(p2
+ 6p
+ 9) = Ф(p)
представим в виде произведения двух
изображений F(p)
=
![]() Ф(p),
которые соответствуют функциям t
e-3t
и 9e3t.
Оригинал решения есть свертка этих
функций: y(t)
=
Ф(p),
которые соответствуют функциям t
e-3t
и 9e3t.
Оригинал решения есть свертка этих
функций: y(t)
=![]() = = 9
= = 9![]() = 9 e3t
= 9 e3t
![]() =
=
![]() = = 9
e3t
{
= = 9
e3t
{
![]() }
= ¼ e3t
- ¼ e
- 3t
- 3/2
t
e-3t
}
= ¼ e3t
- ¼ e
- 3t
- 3/2
t
e-3t
Задачи для самостоятельного решения
Пр. 19 y``- 2y` - y = e3t при условии y(0) = 0 , y`(0) = 0
Ответ:
F(p)
=
![]() ,
y(t)
= 1/16 e-t
- 1/16 e3t
- ¼ t
e3t
,
y(t)
= 1/16 e-t
- 1/16 e3t
- ¼ t
e3t
Пр. 20 y``+ y` - 2 y = et при условии y(0) = 0 , y`(0) = 1
Ответ: F(p) = 1/ (p2 – 1) , y(t) = sh t
Решение систем дифференциальных уравнений
При решении системы ЛДУ с постоянными коэффициентами для каждой неизвестной функции вводится свое изображение и решение задачи сводится к решению системы алгебраических уравнений для изображений.
Рассмотрим систему двух ЛДУ 1 порядка
x`(t) + a11 x(t) + a12 y(t) = f1(t) ( 18 )
y`(t) + a21 x(t) + a22 y(t) = f2(t)
при начальных условиях x(0) = x0, y(0) = y0 . Функции f1(t), f2(t) оригиналы.
Пусть x(t) =: F1(p) , у(t) =: F2(p) , f1(t) =: Ф1(p) , f2(t) =: Ф2(p). Построим изображающее уравнения с учетом формулы ( 6 ) , т.е. x`(t) =: pF1(p) - x0 , y`(t) =: pF2(p) - y0
pF1(p) - x0 + a11 F1(p) + a12 F2(p) = Ф1(p) ( 19 )
pF2(p) - y0 + a21 F1(p) + a22 F2(p) = Ф2(p)
Из решения системы находят F1(p), F2(p), а затем их оригиналы x(t) , y(t) .
Пр.21
При условии x(0)
= y(0)
= 0 решить
систему
![]() .
.
Т.к.
t
=: 1/p2
(Пр.5), то
система ( 18 ) принимает вид
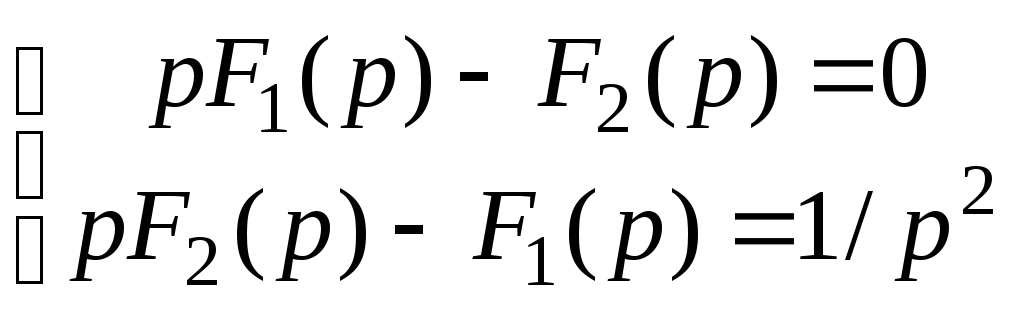
Решение
системы F1(p)
=![]() ; F2(p)
=
; F2(p)
=![]() .
Эти изображения разложим на сумму
простейших дробей: F1(p)
= -
.
Эти изображения разложим на сумму
простейших дробей: F1(p)
= -
![]() +
+
![]() -
-
![]() , F2(p)
= -
, F2(p)
= -
![]() +
+
![]() +
+![]() и по формулам № 1, 3 перейдем к оригиналам,
которые дают решение исходной системы
уравнений :
и по формулам № 1, 3 перейдем к оригиналам,
которые дают решение исходной системы
уравнений :
x(t) = – t + ½ et – ½ e-t , y(t) = – 1 + ½ et + ½ e-t .
Проверка. x`(t) – у(t) = [– 1 + ½ et + ½ e-t] – [– 1 + ½ et + ½ e-t] = 0
у`(t) – x(t) = [½ et – ½ e-t ] – [– t + ½ et – ½ e-t ] = t
