Операции с непрерывными функциями.

Теорема

Если функция и непрерывны в точке , то функции , , так же непрерывны в точке (в случае частного считаем, что в некоторой окрестности ).

Докажем для частного:

где .

ЛЕКЦИЯ №

Очевидно, по определению предела, что тогда , т.е. функция непрерывна в т.  функция вида - непрерывна в точке  многочлен есть непрерывная функция как сумма непрерывных функций. Тк. Точка взята произвольно, то заключаем, что многочлен (целая рациональная функция) непрерывная функция в каждой точке числовой оси.

Теорема непрерывности композиции непрерывных функций.

Если функция непрерывна в т. , а функция непрерывна в т. то сложная функция непрерывна в т. .

К условиям теоремы 2 здесь добавляется непрерывность функции в т. . Учитывая это и применяя теорему 2 имеем

Доказанная теорема, наряду с теоремами 1 и 2 (см. пред. лекцию) систематически используются при вычислении предела непрерывных ункций.

Приращение аргумента и функции в точке, равносильное определение непрерывности.

М

- приращение аргумента в т.

- приращение функции в т.

- приращение значения функции.

Пусть функция непрерывна в т. , тогда

Таким образом можно дать определение непрерывности функции в т. в следующей равносильной форме:

Определение

Функция называется непрерывной в т. если бесконечно малое приращение аргумента в т. вызывает бесконечно малое приращение функции в этой точке.

Непрерывность элементарных функций.

Можно доказать, что все основные элементарные функции непрерывны в области их определения.

Сделаем на примере .

Пусть х – произвольная фиксированная точка числовой оси. Рассмотрим приращение функции в т. х, т.е.

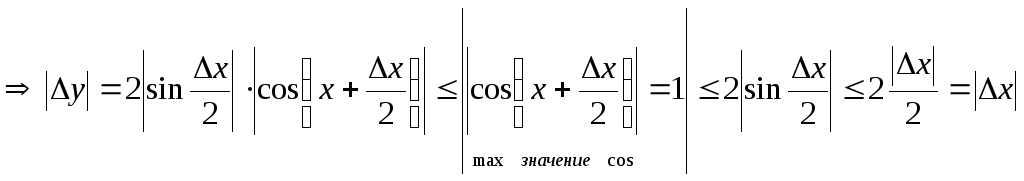
При этом использовано неравенство , для

Ниже будет показано, что при , что можно записать также в виде

Это последнее неравенство не изменится при замене на . Следовательно при будет . Это последнее неравенство очевидно верно и при , т.к. , а .

Итак получено:

, что можно записать также в виде . Тогда (использована теорема о двух легавых) , т.е. функция непрерывна в т. х.

А т.к. точка выбрана произвольно, то заключаем, что функция непрерывна на всей числовой оси.

Элементарной функцией называется всякая функция составленная из основных элементарных функция при помощи конечного числа арифметических действий и композиций.

Так как основные элементарные функции непрерывны в области их определений, а сложение, вычитание, умножение, и деление и композиция непрерывных функций приводят к непрерывным функциям, то заключаем, что всякая элементарная функция непрерывна в области определения.

Два замечательных предела.

Покажем, что (1)

Где х – измеряется в радианах.

Рассмотрим окружность радиуса R=1 и центральный угол

A Х 0 С В D

т.к. хорда окружности меньше стягиваемой ею дуги, т.е. , откуда , т.е. , для

С другой стороны площадь кругового сектора ОАВ меньше площади . или . Поэтому для т.к. для

или (2)

Эти последние неравенства не изменятся при замене х на –х, т.е. они будут справедливы в проколотой - окрестности т. х=0.

Так как функция непрерывна в т. х=0, т.е. , то из неравенств (2) с учетом теоремы о lim двух легавых вытекает формула (1).

Примеры:

1)

2)

Л ЕКЦИЯ №

Т.е. формула (2) полностью доказана.

Полагая в формуле 2 (если ) и применяя теорему о замене переменной в пределе получим другое представление 2 замечательного предела:

(2’)

Следствия:

1) (3) - третий замечательный предел.

Запишем второй замечательный предел по формуле (2’) в виде.

и прологарифмируем его по основанию e: здесь так как функция ln(u) непрерывна в точке u=e, то переставляя местами знак предела и знак непрерывной функции получим: или

2) (4)

здесь в частности при (4’)

Положим

Откуда ; при т.к. показательная функция непрерывна в точке x=0. Пользуясь теоремой о замене переменной в пределе и формулой (3) имеем

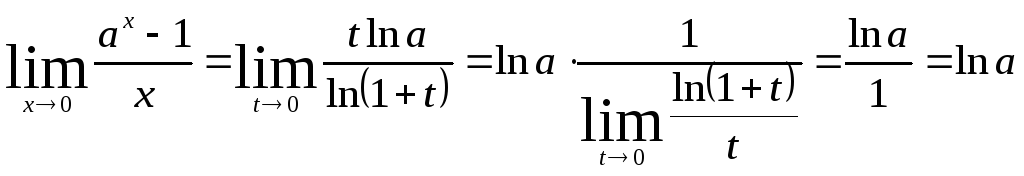
Полагая в формуле (4) a=e приходим к формуле (4’)

3) где

Положим (при в силу непрерывности экспоненциальной функции) ; Имеем:

Применяя теорему о замене переменной в пределе и формулу (4’).

Показательно-степенная функция.

Для вычисления пределов функций вида следует пользоваться формулой:

(6)

При этом считаем, что и существует.

Достаточно применить основное логарифмическое тождество и непрерывность экспоненциальной функции.

Часто встречается случай когда при Покажем, что формула (6) принимает вид: (7)

( при )

Имеем: применяя формулу (3) и 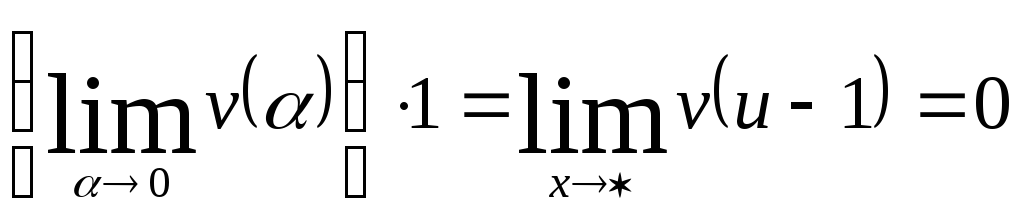. Особенно часто формула (7) применяется когда , т.е. для раскрытия неопределенности .

Примеры применения формул.

1)

2)