4. Принципы моделирования

1. Адекватность, то есть соответствие свойств модели свойствам объекта.

2. Соответствие модели решаемой задаче.

3. Снижение сложности при учете основных свойств системы (абстрагирование от второстепенных свойств).

4. Соответствие сложности и точности модели.

Для упрощения модели используются:

1. сокращение числа входов и выходов системы. Малозначительные входы и выходы системы исключаются или объединяются;

2. изменение физики параметров на модели. Переменные параметры рассматриваются как постоянные, дискретные как непрерывные;

3. изменение физики взаимосвязей между параметрами (например, не учитывается вероятностный характер);

4. ослабление ограничений;

5. снижение требуемой точности.

1. Баланс между погрешностями различных типов (систематической, абсолютной, относительной, приведенной).

2. Многовариантное моделирование, то есть использование различных подходов с выбором оптимального подхода.

3. Модульность моделей сложных систем, предполагает построение общей модели при помощи подмоделей, что дает возможность использовать накопленный опыт.

5. Основные подходы к моделированию

1. Непосредственный анализ функций системы.

2. Проведение полного или частичного эксперимента.

3. Исследование аналога.

4. Анализ имеющейся статистической информации.

4. Математическое моделирование сложных систем

1. Модели сложных систем, используя нечеткую логику

1. Основные понятия

Пусть U – некоторое полное множество, включающее понятие некоторой предметной области. Тогда нечеткое множество F, является подмножеством множества U, определяется при помощи функции принадлежности.

Функция принадлежности отображает элементы на множество действующих чисел в интервале [0.1] и характеризует степень отношения элементов к нечеткому множеству F.

Пусть полное множество U содержит элементы .

,

где «+» – это знак объединения;

«/» – ставит в соответствие каждому элементу значение соответствующей функции принадлежности.

Пример:

Пусть полное множество U – процентные ставки по предмету на приобретение жилья.

Нечеткое множество – низкие процентные ставки, имеет вид:

Высокие ставки:

Ф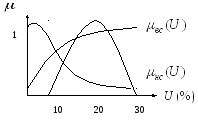ункция принадлежности обычно определяется экспертами (0, 0.1, 0.7, 0.8, 0.9)

2. Основные операции с нечеткими множествами

Пересечение нечетких множеств A и B, принадлежащих полному множеству U – нечеткое множество максимально возможное, которое включает элементы, принадлежащие одновременно и множеству A и множеству B.

Для любого ,

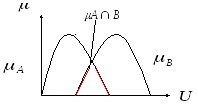
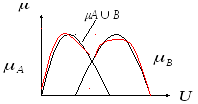
Объединение нечетких множеств A и B, принадлежащих полному множеству U – называется нечетким множеством, которое включает элементы, как множества A, так и множества B.

Для любого ,

3. Нечеткие логические выводы

Четким продукционным правилом называется следующее выражение:

Если .

Нечетким продукционным правилом называется следующая конструкция:

Если X есть A и Y есть B, то Z есть C;

X, Y – входные переменные;

Z – выходная переменная;

A, B и C – нечеткие множества.

Задачей нечеткого логического вывода является на основании заданных четких значений входных характеристик системы, определить четкое значение его выхода.

Алгоритм нечеткого логического вывода включает четыре этапа:

1. Приведение к нечеткости (фазификация).

2. Логический вывод.

3. Композиция.

4. Приведение к четкости (дефазификация).

Пусть система описана при помощи двух нечетких продукционных правил:

1. Если X есть A1 и Y есть B1, то Z есть C1.

2. Если X есть A2 и Y есть B2, то Z есть C2.

Пусть X – доля рынка предприятия, Y – темп роста отрасли, а Z – объем инвестиций в предприятие.

1. Если X, Y, то Z.

2. Если X, Y, то Z (если доля рынка маленькая, темп роста отрасли средний, то инвестиции средние).

1)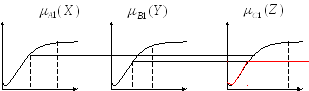

10% 20% x, % 5% 10% y, % 100 z, млн. руб.

большую долю 20% высокий темп роста 10% большие инвестиции

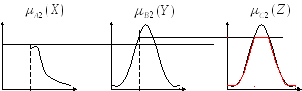
2)

X0 =10% Y0 =5% 100 z, млн. руб.

незначительная доля средний темп роста средний объем инвестиций

Пусть x = 10%, y = 5%, необходимо определить, сколько инвестировать в млн. руб.

Z0 Z

центр тяжести фигуры

Фазификация – определяется степенью истинности предпосылок каждого правила для заданных входов X0, Y0, то есть определяются значения А1(X0), В1(Y0), А2(X0), В2(Y0).

Нечеткий логический вывод – находятся уровни отсечения по каждому правилу:

1) ;

2) .

Находящиеся усеченные функции принадлежности:

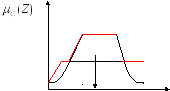
Композиция – усеченные функции принадлежности правой части правил:

Дефазификация (приведение к четкости)– позволяет получать четкие значения входа z, которое соответствует нашим значениям.