4.3.6 Метод потенциальных функций

Название метода связано с аналогией: пусть распознается два образа. Объекты являются точками некоторого пространства X. В эти точки будем помещать заряды , если объект принадлежит образу и образу . Функцию, описывающую распределение электростатического потенциала в таком поле можно использовать для распознавания (построение решающего правила). Если потенциал в точке X создаваемый единичным зарядом находится в , равен K (X; ), то общий потенциал в точке X созданный зарядами равен:

,

где K (X; ) – потенциальная функция.

Данный метод иллюстрирует рисунок:

- некоторые образы;

------ - потенциальная функция, порождаемая одиночным объектом;

____ - суммарная потенциальная функция, порождаемая обучающей последовательностью.

Чаще всего в виде потенциальной функции используется функция, имеющая максимум при образе и монотонно убывающая до нуля. При норме стремящейся к бесконечности:

При предъявлении новых объектов рассматривается новый потенциал.

Если g(x*) > 0, то объект относится к классу 1.

Если g(x*) < 0, то объект относится к классу 2.

Недостаток: сложность реализации при наличии большого количества классов.

4. Локально-ситуационные модели сложных систем

Метод основан на гипотезе «монотонности пространства решений»: похожие входные ситуации приводят к похожим результатам системы.

Рассмотрим алгоритм на примере статического однофакторного объекта (один вход один выход), тогда модель строится в два этапа.

Пусть имеет место пассивный эксперимент. На первом этапе «начальный эксперимент» фиксируется N значений (x – вход, y – выход). На втором этапе, объем которого за ранее не определен, для каждой новой точки x*, y* в N определяется М ближайших точек (узлов) x*.

По данным узлам строится аппроксимированная зависимость обычно линейного вида. По данной зависимости определяется выход модели . Проверяется неравенство < d, где d – заданная точность модели. Если неравенство выполняется, то опыт признается удачным и точка (x*,y*) отбрасывается. Если неравенство не выполняется, то данная точка включается в базу данных N. Это происходит до тех пор, пока не будет подряд отброшено точек. задается заранее.

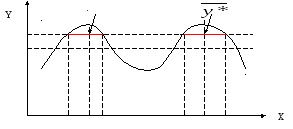
X1 X*=X5 X2 X3 X* X4

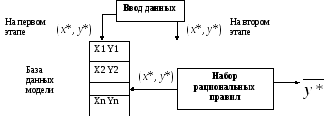
На втором этапе построение модели для каждой вновь вводимой точки (x*,y*) блок «набор решающих правил» выделяет в базе данных модели, строит аппроксимированную зависимость, вычисляет выход модели и принимает решения, нужно ли включать данную точку в базу данных модели. При исключении модели выход системы определяется по предъявленному входу на основе выбранных ближайших узлов и аппроксимированной зависимости. Построенная модель представляет собой базу экспертных значений.

Преимущество: может моделировать систему, простота компьютерной реализации.

4. Многокритериальный выбор альтернатив на основе теории нечетких множеств

Часто принимаемое решение характеризуется при помощи нескольких показателей качества.

Пусть имеется три альтернативы, и . Каждое альтернативное решение характеризуется показателями качества:

• - снижаем цену на товар;

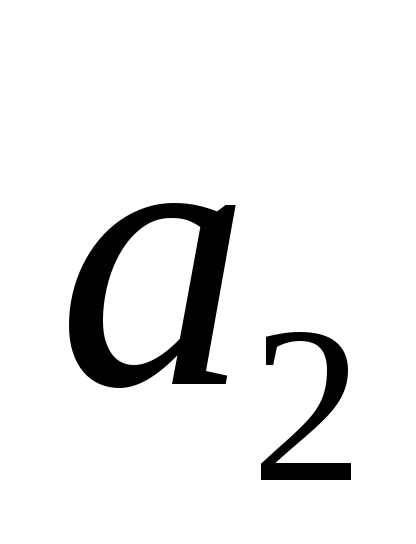• - без изменений;

• - повышение цены.

При этом рассматриваются следующие критерии:

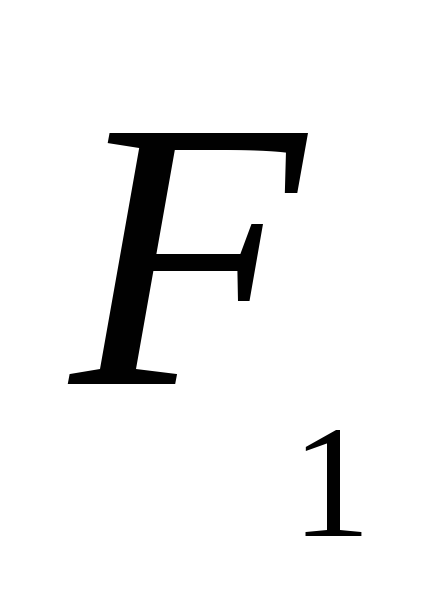• - повышение доли рынка;

• - прибыль;

• - отношение потребителей;

• - коэффициент абсолютной ликвидности.

Пусть для каждой альтернативы определены конкретные значения критериев качества.

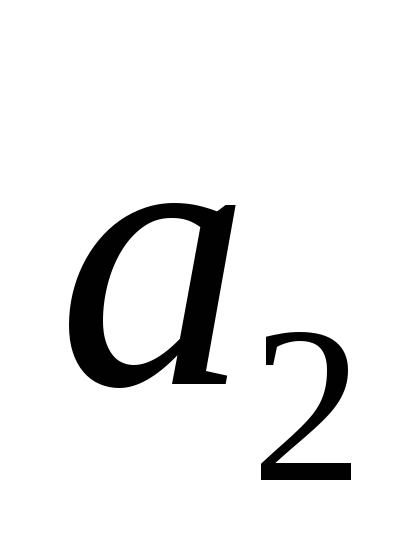
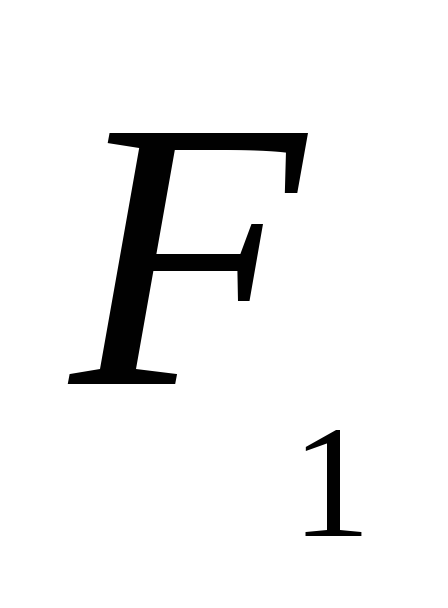, %	60	40	30
, млн. руб.	15	20	25
, %	50	30	40
, ед.	0,1	0,3	0,2

Строится функции принадлежности, характеризующие нечеткие множества желаемых значений показателя качества (желаемая доля рынка).

40% 50% 100%

Для каждого представления в таблице показателя качества по каждой альтернативе определяется значение функции принадлежности указанной нечетким множеством.

Оптимальная альтернатива определяется на основе пересечения нечетких множеств.

Тогда - по столбцам определяем минимальный выигрыш. Оптимальная альтернатива определяется как ; 0,4 – альтернатива два.

Нужно выбрать решение два. Данный пример относится к случаю, когда критерии равнозначны. Если критерии не равнозначны, то используются новые коэффициенты, полученные на основе метода парных сравнений критериев.