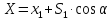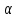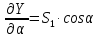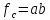Министерство Образования РБ УО «Полоцкий Государственный Университет»

Кафедра геодезии и кадастров

ТМОГИ. Лабораторная работа №3

Обработка косвенных результатов измерений

Вариант 10

Выполнил: Самусенков Д.Н.

Проверил: Дегтярев А.М.

Новополоцк

2007

Оценка точности косвенных измерений

Суть прямой задачи теории погрешностей: нахождение среднеквадратической погрешности функции известного вида, если заданы погрешности ее аргументов , представляющие собой непосредственно измеренные величины.

Основные формулы:

Дисперсия функции

Вектор-строка

20. Вычислить относительную ошибку гипотенузы прямоугольного треугольника, если

, .

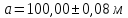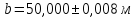Дано: , , , .

Найти: .

Решение. Гипотенуза прямоугольного треугольника будет равна

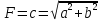
Найдем частные производные для этой функции по параметрам и .

Вычислим относительную ошибку гипотенузы:

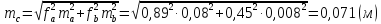
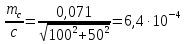
Ответ: .

30. Площадь участка определяется двумя обводами с помощью планиметра. Какова будет предельная ошибка в площади, если каждый отсчет имеет ошибку деление, а цена деления планиметра, равная , не содержит ошибки?

Дано: , ,

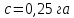
Найти: .

Решение. Запишем формулу для определения площади при помощи планиметра:

Найдем частные производные по отсчетам :

Вычислим относительную ошибку определения площади при помощи планиметра:

Ответ: .

40. Сколько углов должно быть в многоугольнике, чтобы при измерении углов теодолитом четырьмя приемами предельная невязка была не более ?

Дано: ,

Найти:

Решение. Предельная невязка находится по формуле:

где — вероятностный коэффициент (примем его за 2,5), — погрешность прибора (в нашем случае ). Выразим и вычислим количество углов многоугольника

Ответ: сторон в полигоне.

50. Определить относительную ошибку периметра полигона, состоящего из сторон длинной в среднем каждая, если относительная погрешность измерения лентой всех сторон одинакова и равна .

Дано: , ,

Найти:

Решение. В данном случае периметр полигона находится по формуле:

Частная производная функции по равна

Вычислим относительную ошибку периметра полигона:

Ответ: .

1. Определить в общем виде предельную погрешность приращения координат по оси абсцисс.

Решение: Формула приращения координат по оси абсцисс имеет вид

где - длина линии, - дирекционный угол.

Формула предельной погрешности будет иметь вид

где 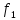и — частные производные от функции по и соответственно.

Находим частные производные:

Тогда формула предельной погрешности примет окончательный вид:

Ответ: .

Оценка точности вектор-функции

Суть оценивания заключается в необходимости производства оценки не одной функции, а нескольких, описывающих совместно какой-либо процесс.

Основные формулы.

Вектор-функция

Оценка вектор-функции в виде ковариационной матрицы

5. Угол получен как среднее арифметическое из четырех приемов со среднеквадратической погрешностью, а угол — из девяти приемов со среднеквадратической погрешностью одного приема. Найти среднюю квадратическую погрешность суммы углов и.

Дано: , , ,

Найти:

Решение. Вычислим погрешность измерения угла из приемов:

Запишем функцию, погрешность которой нужно найти:

Для того, чтобы найти ее погрешность, найдем частные производные по каждому углу и по формуле вычислим среднюю квадратическую погрешность:

Ответ: .

10. Найти ковариационную матрицу и коэффицент корреляции для определения координат в однократной линейной засечке при , , а базис безошибочен и имеет значение .

Дано: , , , ,

Найти: , .

Решение.

Составим уравнения для определения координат:

Составим вектор-функцию:

В вектор-функции частные функции содержат общие элементы — расстояние и дирекционный угол , поэтому они будут коррелированны между собой.

Найдём матрицу Якоби. Для этого вычислим частные производные от по и :

Находим дирекционный угол по формуле:

где найдём по теореме косинусов:

Откуда:

Матрица Якоби примет вид:

Найдем матрицу измерений:

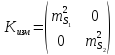
Теперь получим ковариационную матрицу частных функций:

Найдем коэффициент корреляции :

Ответ: , .

3. Вычислить коэффициент корреляции между приращениями координат по осям абсцисс и ординат, если результаты измерений следующие: длина , дирекционный угол

.

Дано: ,

Найти: .

Решение. Запишем частные и общую вектор-функцию:

В вектор-функции частные функции содержат общие элементы — расстояние и дирекционный угол , поэтому они будут коррелированны между собой.

Найдём матрицу Якоби. Для этого вычислим частные производные от по и :

Матрица Якоби примет вид

Найдём матрицу измерений:

Получаем ковариационную матрицу частных функций по формуле:

Из матрицы найдём коэффициент корреляции

Ответ: .

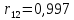Предрасчет точности измерений по заданной погрешности функции (Задача проектирования)

Вторая задача теории погрешностей измерений используется для проектирования точностей, с которыми необходимо производить измерение параметров для достижения общей точности, максимально приближенной к заданной.

Основные формулы.

Дисперсии для трех случаев применения принципа равных влияний:

Погрешности трех случаев применения принципа равных влияний:

10. Для производства угловых измерений в полигонометрии получено три теодолита. Первый теодолит результат со средней квадратической погрешностью измерения угла одним приемом, равной , второй — равной , третий — с погрешностью, равной . Определить какое минимальное число приемов нужно сделать каждым теодолитом, чтобы обеспечить получение средней квадратической погрешности вероятнейшего значения угла не более .

Дано: , , ,

Найти: , ,

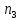
Решение. Для того, чтобы найти количество приемов воспользуемся следующей формулой:

где 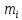— точность, с которой был получен угол в один прием, — количество приемов.

Выразим количество приемов из этой формулы и найдем их для каждого теодолита.

Ответ: , , .

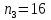20. При проектировании результатов измерений по первому принципу (равенство погрешностей измерений) требуется получить площадь прямоугольника с погрешностью при соотношении сторон 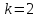и погрешности измерения стороны . Найти длины сторон прямоугольника и , удовлетворяющие поставленному условию на погрешность площади.

Дано: , ,

Найти:

Решение. Составим функцию площади прямоугольника:

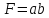
Учитывая то, что отношение сторон по длине , получим

Найдем частную производную

Замишем формулу погрешности и подставим все имеющиеся данные

Выразим сторону и вычислим ее:

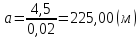
Зная соотношение, вычислим величину стороны :

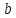Ответ: , .

30. Определить средние квадратические погрешности измерения ребер прямоугольного параллелепипеда 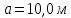, и , при которых его объем будет получен с погрешностью .

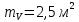Дано: , , ,

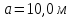Найти: , ,

Решение. Составим функцию объема параллелепипеда:

Найдем частные производные по каждой из сторон:

Вычислим погрешности по трем методам:

1)

2)

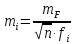
3)