
- •Тема 3. Методи розв’язування
- •1) Метод Гаусса-Жордана
- •Порядок заповнення розрахункової таблиці:
- •Алгоритм -го кроку методу Гаусса-Жордана
- •2) Похибки розв’язування систем лінійних алгебраїчних рівнянь методом Гаусса-Жордана
- •2) Інші прямі методи
- •2. Ітераційні методи розв’язування систем лінійних алгебраїчних рівнянь
- •Метод простої ітерації
- •4. Умови збіжності методу простої ітерації
- •Метод Зейделя
- •Тема 4. Методи розв’язування нелінійних рівнянь
- •1. Постановка задачі розв’язування нелінійного рівняння з одним невідомим. Відокремлення коренів.
- •Відокремлення коренів.
- •Способи відокремлення коренів
- •2. Метод поділу відрізку пополам (метод бісекції)
- •Алгоритм знаходження кореня рівняння методом поділу відрізку пополам
- •3. Метод хорд
- •Алгоритм знаходження кореня рівняння методом хорд
- •4. Метод дотичних (метод Ньютона)
- •Алгоритм знаходження кореня рівняння методом дотичних
- •5. Метод простих ітерацій
- •Алгоритм знаходження кореня рівняння методом простих ітерацій
3. Метод хорд
Нехай
знайдений такий відрізок
![]() ,
що
,
що
![]() ,
і на кінцях відрізку функція
,
і на кінцях відрізку функція
![]() ,
яка визначає рівняння
,
яка визначає рівняння
![]() ,
набуває значення різних знаків, тобто
,
набуває значення різних знаків, тобто
![]() .
.
Метод
хорд (його
ще називають методом лінійного
інтерполювання) при
тих самих припущеннях забезпечує
більш швидке знаходження кореня, чим
метод поділу
відрізку пополам. Для цього відрізок
![]() ділиться не пополам, а у відношенні
ділиться не пополам, а у відношенні
![]() .
.
Геометрично
метод хорд еквівалентний заміні кривої
![]() хордою, яка проходить через точки
хордою, яка проходить через точки
![]() і
і
![]() .
За наближення кореню рівняння (1)
приймаються значення
абсциси точки перетину хорди,
що проходить через точки
.
За наближення кореню рівняння (1)
приймаються значення
абсциси точки перетину хорди,
що проходить через точки
![]() і
і
![]() з віссю
з віссю
![]() :
:

Рівняння
хорди
![]() ,
як рівняння прямої, що проходить через
дві задані точки, має вигляд:
,
як рівняння прямої, що проходить через
дві задані точки, має вигляд:
 .
.
Покладемо
![]() і
і
![]() ,
тоді отримаємо6
,
тоді отримаємо6

Припустимо, що виконуються наступні умови:
1)
![]() на
на
![]() неперервна разом із своїми похідними
неперервна разом із своїми похідними
![]() і
і
![]() ;
;
2)
![]() ;
;
3)
![]() і
і
![]() зберігають кожна певний знак на
зберігають кожна певний знак на
![]() .
.
Розглянемо
два випадки:
![]() ,
,
![]() і
і
![]() ,
,
![]() .
Випадок
.
Випадок
![]() зводиться до розглядуваного, якщо
рівняння записати у формі
зводиться до розглядуваного, якщо
рівняння записати у формі
![]() .
.
Першому випадку (мал.1) відповідає формула:
![]() ;
;
 ,
,
![]() (3)
(3)
а другому (мал.2):
![]() ;
;
 ,
,
![]() (4)
(4)


1) 2)
В
першому випадку залишається
нерухомим кінець
![]() ,
а
в другому
– кінець
,
а
в другому
– кінець
![]() .
Для виявлення нерухомого кінця
використовується умова
.
Для виявлення нерухомого кінця
використовується умова
![]() ,
де
,
де
![]() або
або
![]() .
Якщо нерухомий кінець
.
Якщо нерухомий кінець
![]() ,
застосовується формула (3), а якщо кінець
,
застосовується формула (3), а якщо кінець
![]() – формула (4).
– формула (4).
Алгоритм знаходження кореня рівняння методом хорд
-
Задати початкове наближення
 так, щоб виконувалася умова
так, щоб виконувалася умова
 ,
де
,
де
 або
або
 .
Задати точність
.
Задати точність
 .
Покласти
.
Покласти
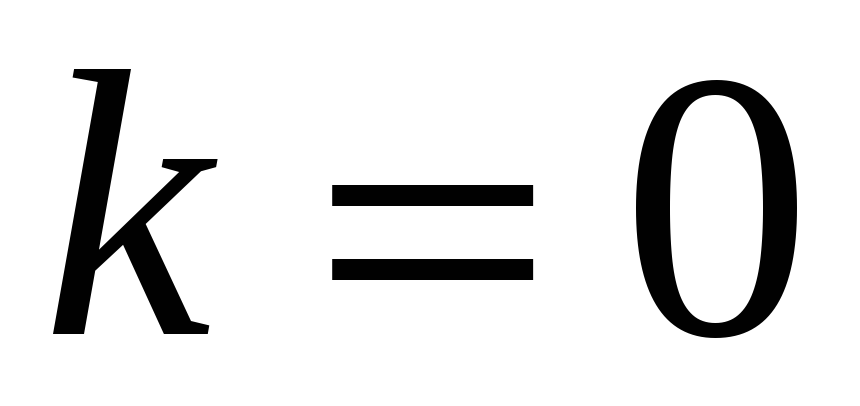 .
. -
Якщо
 ,
то обчислюємо
,
то обчислюємо
 за формулою (3), якщо
за формулою (3), якщо
 ,
то обчислюємо
,
то обчислюємо
 за формулою (4).
за формулою (4). -
Якщо
 ,
процес закінчити і покласти
,
процес закінчити і покласти
 .
.
Якщо
![]() ,
покласти
,
покласти
![]() і перейти до п.2.
і перейти до п.2.
Приклад
5.
Знайти корінь рівняння
![]() (див. приклад 1) методом
хорд з точністю
(див. приклад 1) методом
хорд з точністю
![]() .
.
Розв’язання.
В прикладі 1 корінь рівняння був
відокремлений:
![]() .
Очевидно, функція неперервна на відрізку
.
Очевидно, функція неперервна на відрізку
![]() разом із своїми похідними
разом із своїми похідними
![]() ,
,
![]() .
Оскільки
.
Оскільки
![]() ,
,
![]() ,
а
,
а
![]() на відрізку
на відрізку
![]() ,
то
,
то
![]() і маємо другий
випадок. Результати
розрахунків з використанням формули
(4) зведемо в таблицю:
і маємо другий
випадок. Результати
розрахунків з використанням формули
(4) зведемо в таблицю:
-



0
–2
1
–1,1666
0,8334
2
–1,3953
0,2287
3
–1,2991
0,0962
4
–1,3347
0,0356
5
–1,3209
0,0138
6
–1,3261
0,0052
7
–1,3241
0,0020
8
–1,3248
0,0007
Оскільки
![]() ,
то процес завершується: корінь
рівняння
,
то процес завершується: корінь
рівняння
![]() .
.
