23

Розділ 2

Чисельні методи алгебри

Тема 3. Методи розв’язування

систем лінійних алгебраїчних рівнянь

1. Прямі методи розв’язування

систем лінійних алгебраїчних рівнянь.

Розглянемо чисельні методи розв’язання системи лінійних алгебраїчних рівнянь

(1)

Запишемо цю систему у матричній формі:

(2)

де

– квадратна -матриця:;

– матриця-стовпець невідомих (шуканий вектор);

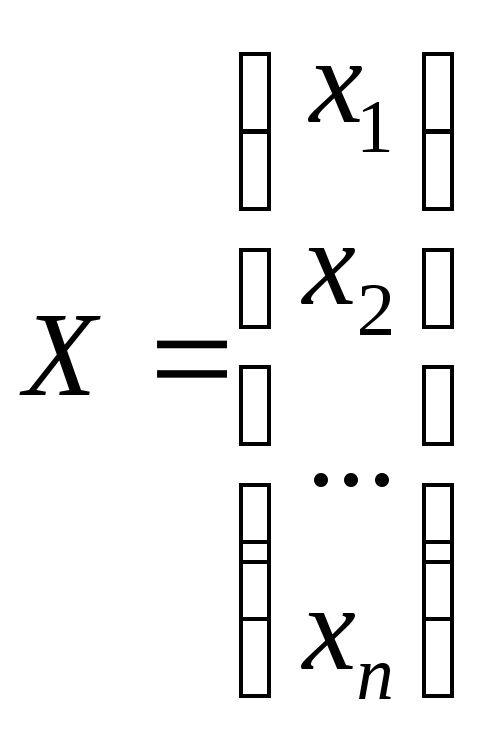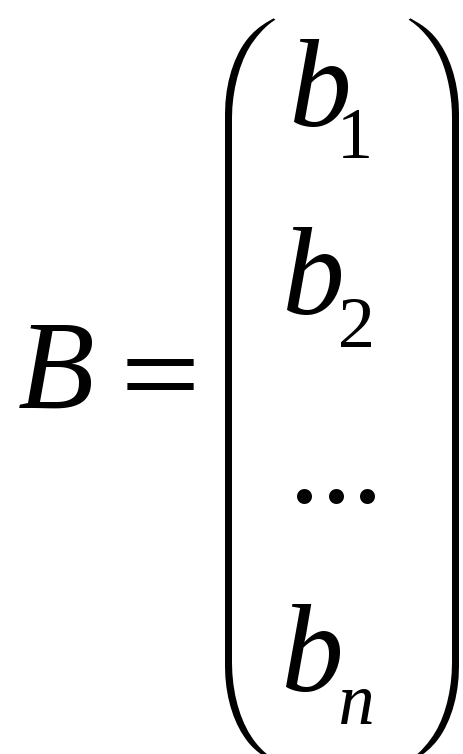– матриця-стовпець вільних членів (заданий вектор).

Припускаємо, що , та визначник матриці відмінний від нуля, так що існує єдиний розв’язок . З курсу лінійної алгебри відомо, що систему (1) можна розв’язати за формулами Крамера. Для великих цей спосіб практично нереалізований тому, що потребує порядку арифметичних дій. Тому широко використовуються інші методи розв’язання, наприклад, метод Гаусса, який потребує дій. На цей час метод Гаусса та його модифікації залишаються одними з найкращих методів розв’язування систем лінійних алгебраїчних рівнянь.

Методи чисельного розв’язання системи (1) поділяються на дві групи:

- прямі методи;

- ітераційні методи.

У прямих (або точних) методах розв’язок системи (1) відшукується за скінченну кількість арифметичних дій. Внаслідок похибок округлення прямі методи насправді не приводять до точного розв’язку системи (1) і назвати їх точними можливо лише залишаючи осторонь похибки округлення.

1) Метод Гаусса-Жордана

Звичайний метод Гаусса полягає у приведенні системи (1) до трикутного вигляду. Це досягається послідовним виключенням невідомих , , ..., системи шляхом її елементарних рівносильних перетворень. При цьому при чисельному розв’язуванні системи перетворенню піддаються не самі рівняння, а вихідні дані – матриця і вектор , об’єднані в одну розширену матрицю .

Однією з найбільш розповсюджених модифікацій метода Гаусса є метод Гаусса-Жордана або метод повного виключення. Основна ідея методу Гаусса-Жордана. полягає в тому, щоб на черговому кроці виключати не наступне за номером невідоме, а те невідоме, коефіцієнт при якому є найбільшим за модулем. Тим самим, якщо , то в процесі обчислень не буде відбуватися ділення на нуль.

Перетворення методу Гаусса-Жордана приводять матрицю системи (1) до одиничної матриці.

На практиці при розв’язуванні системи лінійних алгебраїчних рівнянь методом Гаусса-Жордана зручно користуватися розрахунковою таблицею, яка називається схемою Гаусса-Жордана.

Порядок заповнення розрахункової таблиці:

На нульовому кроці в стовпцях таблиці записуємо коефіцієнти системи, вільні члени. Підсумовуємо всі елементи по рядках і записуємо суму у відповідний стовпець.

Обчислення на всіх інших кроках здійснюються за наступним алгоритмом:

Алгоритм -го кроку методу Гаусса-Жордана

1. Обираємо ведучий елемент 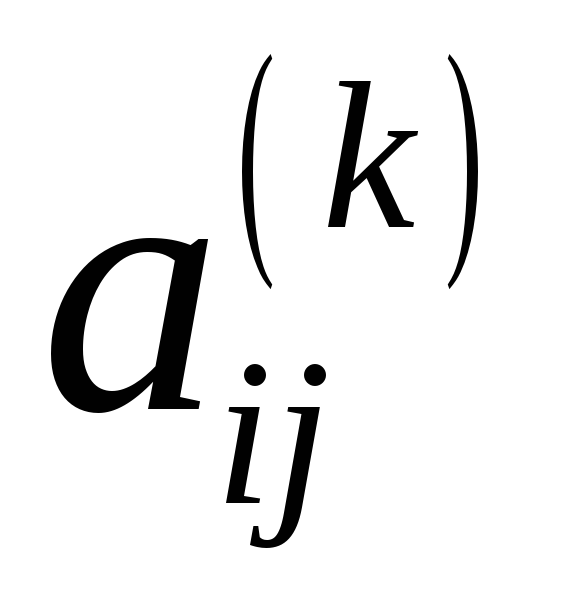. Для спрощення обчислень зручно за ведучий обрати елемент, який дорівнює одиниці. Якщо такого нема, за ведучий обирається елемент, найбільший за модулем. Рядок і стовпець, на перетині яких знаходиться ведучий елемент, називається ведучим рядком і ведучим стовпцем відповідно. (На схемі для визначеності взято за ведучий елемент .)

2. Ділимо всі елементи ведучого рядка на ведучий елемент , .

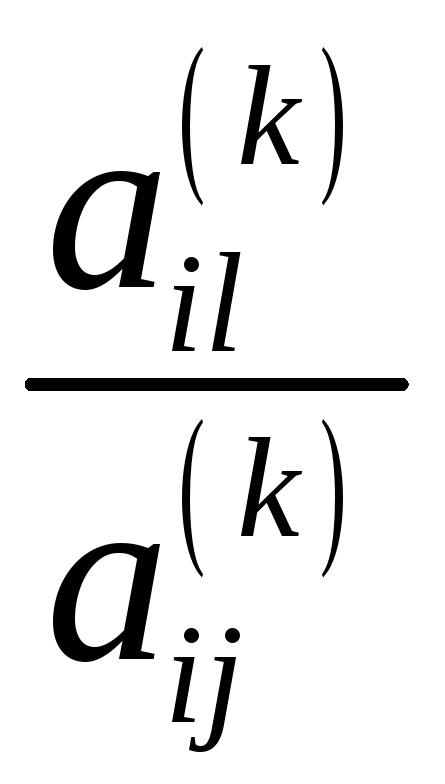3. Всі елементи ведучого стовпця замінюються нулями, ведучий елемент замінюється одиницею.

4. Усі інші елементи розрахункової таблиці, в тому числі і контрольного стовпця, знаходяться за формулою:

; (5)

, , , .

Схематично правило обчислення елементів можна зобразити у вигляді прямокутника:

5. Для перевірки правильності розрахунків обчислюємо суму елементів кожного рядка і порівнюємо її з відповідним елементом контрольного стовпця, який обчислюється за формулою (5). Якщо обчислення виконані правильно, то елементи двох останніх стовпчиків таблиці дорівнюють один одному.

Приклад 1. Методом Гаусса-Жордана розв’язати систему лінійних алгебраїчних рівнянь

Розв’язання. Всі обчислення відбуваються за схемою Гаусса-Жордана:

Крок	Коефіцієнти при невідомих			Вільні члени	Суми по рядках	Контроль
0	2	–1	1	3	5
	1	1	–2	1	1
	0	1	2	8	11
1	0	–3	5	1	3	3
	1	1	–2	1	1	1
	0	1	2	8	11	11
2	0	0	8	25	33	33
	1	0	3	7	11	11
	0	1	1	8	11	11
3	0	0	1	2,273	4,125	4,125
	1	0	0	2,091	3,375	3,375
	0	1	0	3,455	5,875	5,875

Отже, розв'язком системи є , , .

Число арифметичних множення і ділення дій, що необхідні для розв’язання системи за допомогою методу Гаусса-Жордана дорівнює .