
- •Тема 3. Методи розв’язування
- •1) Метод Гаусса-Жордана
- •Порядок заповнення розрахункової таблиці:
- •Алгоритм -го кроку методу Гаусса-Жордана
- •2) Похибки розв’язування систем лінійних алгебраїчних рівнянь методом Гаусса-Жордана
- •2) Інші прямі методи
- •2. Ітераційні методи розв’язування систем лінійних алгебраїчних рівнянь
- •Метод простої ітерації
- •4. Умови збіжності методу простої ітерації
- •Метод Зейделя
- •Тема 4. Методи розв’язування нелінійних рівнянь
- •1. Постановка задачі розв’язування нелінійного рівняння з одним невідомим. Відокремлення коренів.
- •Відокремлення коренів.
- •Способи відокремлення коренів
- •2. Метод поділу відрізку пополам (метод бісекції)
- •Алгоритм знаходження кореня рівняння методом поділу відрізку пополам
- •3. Метод хорд
- •Алгоритм знаходження кореня рівняння методом хорд
- •4. Метод дотичних (метод Ньютона)
- •Алгоритм знаходження кореня рівняння методом дотичних
- •5. Метод простих ітерацій
- •Алгоритм знаходження кореня рівняння методом простих ітерацій
2. Метод поділу відрізку пополам (метод бісекції)
Нехай
дано рівняння
![]() і відокремлений простий корінь
і відокремлений простий корінь
![]() ,
тобто знайдений такий відрізок
,
тобто знайдений такий відрізок
![]() ,
що
,
що
![]() ,
і на кінцях відрізку функція
,
і на кінцях відрізку функція
![]() ,
яка визначає рівняння
,
яка визначає рівняння
![]() ,
набуває значення різних знаків, тобто
,
набуває значення різних знаків, тобто
![]() .
Відрізок
.
Відрізок
![]() називається початковим
інтервалом невизначеності, тому
що відомо, що корінь йому належить, але
його місцеположення
з заданою точністю не визначено.
називається початковим
інтервалом невизначеності, тому
що відомо, що корінь йому належить, але
його місцеположення
з заданою точністю не визначено.
Процедура
уточнення положення кореня полягає в
побудові вкладених один в один відрізків,
кожен з яких містить корінь рівняння.
Для цього знаходиться середина поточного
інтервалу невизначеності
 ,
,
![]() ,
і за наступний інтервал невизначеності
з двох можливих обирається той, на кінцях
якого функція
,
і за наступний інтервал невизначеності
з двох можливих обирається той, на кінцях
якого функція
![]() набуває значення різних знаків.
набуває значення різних знаків.

Алгоритм знаходження кореня рівняння методом поділу відрізку пополам
-
Знайти початковий інтервал невизначеності
 одним з методів відокремлення коренів.
Задати точність
одним з методів відокремлення коренів.
Задати точність
 .
Покласти
.
Покласти
 .
. -
Знайти середину поточного інтервалу невизначеності:
 .
.
-
Якщо
 ,
то покласти
,
то покласти
 ,
,
 ,
а якщо
,
а якщо
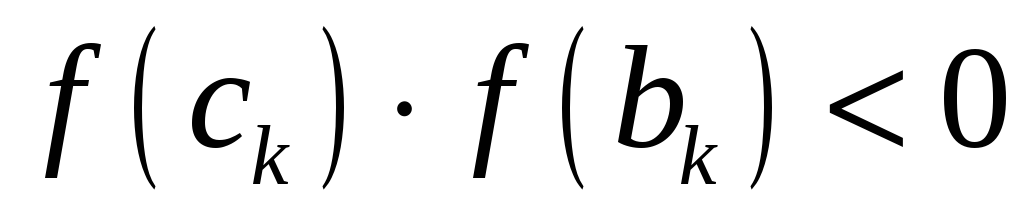 ,
то покласти
,
то покласти
 ,
,
 .
В результаті знайдемо поточний інтервал
невизначеності
.
В результаті знайдемо поточний інтервал
невизначеності .
. -
Якщо
 ,
то процес завершується:
,
то процес завершується:
 .
Наближене значення кореня знаходиться
за формулою:
.
Наближене значення кореня знаходиться
за формулою:
 .
.
Якщо
![]() ,
то покласти
,
то покласти
![]() і перейти до п. 2.
і перейти до п. 2.
Число
ітерацій
![]() ,
необхідних для досягнення заданої
точності
,
необхідних для досягнення заданої
точності
![]() ,
можна оцінити за формулою:
,
можна оцінити за формулою:
 .
.
Звідси
видно, що, наприклад, для досягнення
точності
![]() (при
(при
![]() )
необхідно виконати приблизно 10 ітерацій.
)
необхідно виконати приблизно 10 ітерацій.
Приклад
4.
Знайти корінь рівняння
![]() (див. приклад 1) методом
поділу відрізку пополам з точністю
(див. приклад 1) методом
поділу відрізку пополам з точністю
![]() .
.
Розв’язання.
В прикладі 1 корінь рівняння був
відокремлений:
![]() ,
тому
,
тому
![]() ,
,
![]() .
Очевидно, функція неперервна на відрізку
.
Очевидно, функція неперервна на відрізку
![]() ,
має єдиний простий корінь. На кінцях
відрізку
,
має єдиний простий корінь. На кінцях
відрізку
![]() функція набуває значень
функція набуває значень
![]() ,
,
![]() ,
протилежних за знаком. Результати
розрахунків зведемо в таблиці:
,
протилежних за знаком. Результати
розрахунків зведемо в таблиці:
|
|
|
|
|
|
|
|
|
|
0 |
–5 |
–2 |
–1 |
1 |
–1,5 |
–0,875 |
1 |
|
1 |
–0,875 |
–1,5 |
–1 |
1 |
–1,25 |
0,2965 |
0,5 |
|
2 |
–0,875 |
–1,5 |
–1,25 |
0,2965 |
–1,375 |
–0,224 |
0,25 |
|
3 |
–0,224 |
–1,375 |
–1,25 |
0,2965 |
–1,3125 |
0,05 |
0,125 |
|
4 |
–0,224 |
–1,375 |
–1,3125 |
0,05 |
|
–0,08 |
0,0625 |
|
5 |
–0,08 |
–1,34375 |
–1,3125 |
0,05 |
–1,3282 |
–0,015 |
0,03125 |
|
6 |
–0,015 |
–1,3282 |
–1,3125 |
0,05 |
–1,3204 |
0,018 |
0,0156 |
|
7 |
–0,015 |
–1,3282 |
–1,3204 |
0,018 |
–1,3243 |
0,0018 |
0,00781 |
Оскільки
![]() ,
то процес завершується:
,
то процес завершується:
![]() .
Наближене значення кореня знаходиться
за формулою:
.
Наближене значення кореня знаходиться
за формулою:
 .
.

