4. Умови збіжності методу простої ітерації

Умови збіжності процесу ітерації пов'язані з поняттям норми матриці і вектора. Поняття норми вводиться для оцінки матриці в цілому.

Означення. Нормою матриці називається дійсне число, яке позначається і задовольняє умовам:

1) , причому ;

2) ;

3) , де – деякі матриці (нерівність трикутника);

4) .

Норми матриці можна ввести багатьма способами. Найбільш застосовними є наступні три:

1) перша норма дорівнює максимальній з сум модулів елементів матриці по рядках:

;

для векторів

2) друга норма дорівнює максимальній з сум модулів елементів матриці по стовпцях:

;

для векторів

3) третя норма дорівнює квадратному кореню з суми квадратів елементів матриці по стовпцях:

.

для векторів

Норма називається евклідовою. Для радіус-вектора вона відповідає його довжині.

Відповідь на питання про збіжність методу простих ітерацій дає наступна теорема.

Теорема (достатня умова збіжності методу простих ітерацій). Метод простих ітерацій, який реалізується в процесі послідовних наближень (6), збігається до єдиного розв'язку початкової системи при будь-якому початковому наближенні із швидкістю не менше геометричної прогресії, якщо яка-небудь з норм 1)-3) менше одиниці:

, .

Зауваження. Умови збіжності виконуються, якщо в матриці переважають діагональні елементи, тобто виконуються нерівності:

, , (7)

і хоча б для одного нерівність (7) строга. Інакше, модулі діагональних елементів більше суми модулів недіагональних.

Умови (7) переваги діагональних елементів досягають перестановкою рівнянь системи.

Ітерації перериваються, якщо виконана умова:

, (8)

де – задана точність, яку необхідно досягти при розв’язуванні системи. або більш простіша умова:

. (9)

Теорема (про похибку наближень, які обчислюються за методом простих ітерацій). Якщо в ітераційному процесі норма матриці , менше одиниці (), то справедлива наступна оцінка норми похибки:

Якщо , то

.

На основі останньої нерівності можна записати апріорну оцінку похибки

,

з якої ще до обчислень можна отримати число ітерацій, потрібних для досягнення заданої точності:

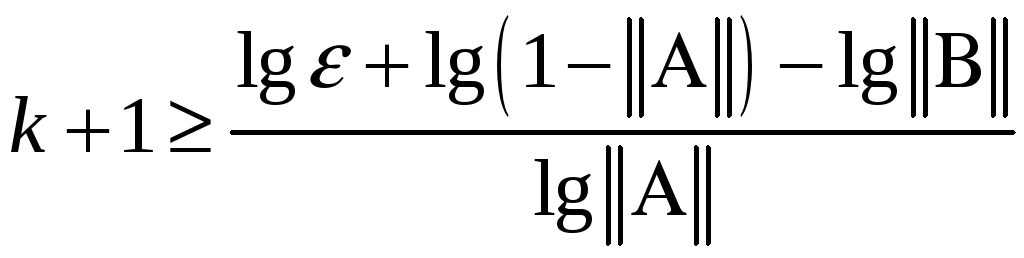(10)

Приклад 3. Методом простих ітерацій розв’язати систему лінійних алгебраїчних рівнянь

з точністю , попередньо оцінивши число ітерацій.

Розв’язання.

1. Перевіримо умову (7) переваги діагональних елементів. Оскільки

, , ,

то умова переваги діагональних елементів не виконується. Переставимо рівняння системи так, щоб умова (7) переваги діагональних елементів виконувалась:

Отримуємо:

, , .

Приведемо систему до вигляду, зручному для ітерацій. Виразимо з першого рівняння системи, – з другого, – з третього. Отримаємо систему:

де

та ,

Оскільки , то достатня умова збіжності виконується. За формулою (10) обчислимо число ітерацій, які забезпечують задану точність:

,

.

Таким чином, для розв’язання задачі потрібно зробити не менше п’яти ітерацій.

1. Задамо початкове наближення .

1. Виконаємо розрахунки за формулою (6) :

,

або

,

до виконання умов збіжності. Результати занесемо в розрахункову таблицю:

0	1,2000	1,3000	1,4000	-
1	0,9300	0,9200	0,9000	0,5
2	1,0180	1,0240	1,0300	0,13
3	0,9946	0,9934	0,9916	0,0384
4	1,0015	1,0020	1,0024	0,0108
5	0,9996	0,9995	0,9993	0,027<

3. Розрахунки закінчено, оскільки виконана умова закінчення:

=0,027<.

Наближений розв'язок . Очевидно, точний розв'язок .