4.3.2 Прямая оценка качества сау. Передаточная функция всей системы имеет вид:

(39)

проведем обратное преобразование Лапласа от передаточной функции САУ.

(40)

График переходного процесса приведен на рисунке 5.

Рисунок 5 – График переходного процесса САУ

По полученному переходному процессу определим прямые показатели качества САУ:

Установившееся значение h_уст=6,3

Тогда 5% интервал отклонения от установившегося значения будет соответствовать следующей величине.

(42)

Перерегулирование

(43)

Время переходного процесса tп=4,2 с.

Время нарастания регулируемой величины (время достижения максимума) tн=4,2 c.

Время первого согласования (время, когда регулируемая величина в первый раз достигает своего установившегося значения) t₁=4,2 c.

Период колебаний Т=∞.

Частота колебаний .

Колебательность (число колебаний за время колебательного процесса) n=0.

Декремент затухания .

4.3.3 Косвенная оценка качества. Для этого построим амплитудно частотную характеристику (см. рисунок 6) выполненную в программе MathCAD.

Рисунок 6 – Амплитудно-частотная характеристика САУ

Резонансная частота (частота при которой АЧХ достигает своего максимального значения) ω_Р=0

Показатель колебательности . (44)

Частота среза – частота, при которой АЧХ достигает значения, равного 1. Следовательно _ср=4,6.

4.3.4 Устойчивость САУ по критерию Шур-Кона. Проверка устойчивости локальной системы регулирования с учетом ЭВМ выполняется на основании критерия устойчивости Шур - Кона, который позволяет анализировать устойчивость дискретных и дискретно-непрерывных систем по характеристическому уравнению замкнутой системы, записанному в форме z-преобразования.

Замкнутая система будет устойчива, если корни характеристического уравнения будут находиться внутри единичной окружности, т.е., если коэффициенты уравнения будут удовлетворять всем определителям Шур - Кона, имеющих отрицательные значения для нечетных определителей и положительных для четных.

Переход от операторной формы записи передаточной функции замкнутой системы к z- форме и расчет определителей Шур - Кона осуществляется при помощи математического редактора MathCAD.

Разложение передаточной функции замкнутой САР выполняется в программе MathCAD:

(45)

Переход от операторной формы к z –форме выполняется по формуле:

W(z) =, (46)

- фиксатор нулевого порядка,

- z –форма непрерывной части системы автоматического регулирования.

Передаточная функция в z-форме имеет вид:

Полученное выражение преобразуется в программе MathCAD:

(49)

Проверка устойчивости передаточной функции в z – форме выполняется по корням характеристического уравнения.

Характеристическое уравнение в z – форме имеет вид:

(50)

Определение корней характеристического уравнения выполняется в программе MathCAD:

(51)

Таким образом, имеем пять корня характеристического уравнения, которые находятся внутри единичной окружности. Следовательно, заданная система автоматического управления является устойчивой.

5 ПОСТРОЕНИЕ ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК САУ

5.1 Построение ЛАЧХ и ЛФЧХ САУ

Для дальнейшего исследования, передаточную функцию разомкнутой системы подвергаем z – преобразованию.

Передаточная функция разомкнутой системы имеет вид:

(52)

(53)

Заменим z на выражение от псевдочастоты : z=, где , получим:

ЛАЧХ и ЛФЧХ нашей системы приведены на рисунке 7.

А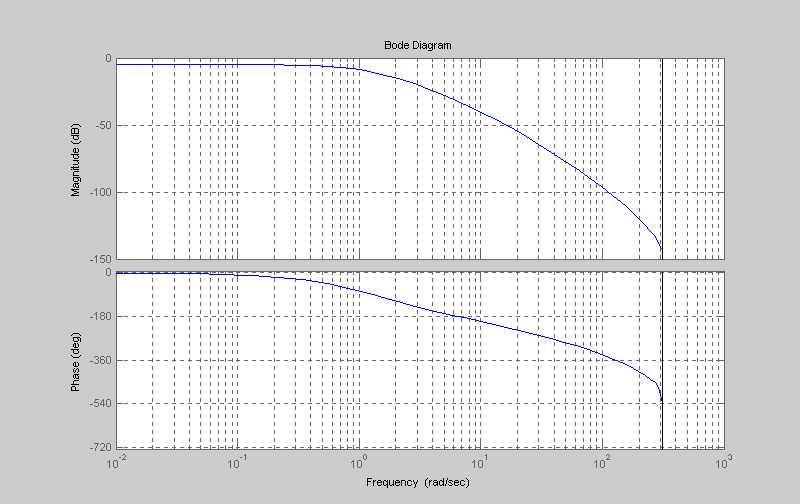

Рисунок 7 – ЛАЧХ и ЛФЧХ разомкнутой системы

5.2 Определение запасов устойчивости САУ

По полученной ЛФЧХ и ЛАЧХ (см. рисунок 7) определяем запасы устойчивости по фазе и амплитуде. Так как ЛАЧХ не пересекается с осью lg(ω), то запас по фазе равен бесконечности. Запас устойчивости по амплитуде 30 дБ. Для обеспечения запасов устойчивости и соответствия условиям технического задания необходимо ввести в ЛСУ корректирующее устройство и повысить коэффициент передачи.

6 ПОСТРОЕНИЕ ЖЛАЧХ САУ, ЛАЧХ КОРРЕКТИРУЮЩЕГО

УСТРОЙСТВА

6.1 Построение ЖЛАЧХ САУ

Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, имеющей желаемые (требуемые) статические и динамические свойства. ЖЛАЧХ состоит из трех основных асимптот: низкочастотной, среднечастотной и высокочастотной. Среднечастотная асимптота ЛАЧХ разомкнутой системы и ее сопряжение с низкочастотной определяют динамические свойства системы – устойчивость и показатели качества переходной характеристики.

Осуществим построение ЖЛАЧХ методом Солодовникова. Зададим параметры желаемой системы:

• время регулирования t_p, с 1,2

• перегулирование σ, % 20

• колебательность 1,2

Определим частоту среза ЖЛАЧХ по номограмме Солодовникова (см. рисунок 8), зная время регулирования, перерегулирования и колебательность САУ, по формуле [11]:

(55)

Откуда при к=2,4

Определим среднечастотную область, с верхней границей (дБ) и с нижней границей (дБ).

Наклон ЖЛАЧХ в среднечастотной области равен –20 дБ/дек. Наклон ЖЛАЧХ в высокочастотной области должен быть близким к наклону исходной ЛАЧХ, в нашем случае он совпадает. ЖЛАЧХ приведена на рисунке 9

Рисунок 8 – Номограмма Солодовникова

Рисунок 9 – ЛАЧХ и ЖЛАЧХ разомкнутой системы

6.2 Построение ЖЛАЧХ корректирующего устройства

Проведем последовательную коррекцию нашей системы. Для получения ЖЛАЧХ корректирующего устройства вычтем из ЖЛАЧХ ЛАЧХ исходной системы.

Рисунок 10 – ЖЛАЧХ корректирующего устройства

7 РАСЧЕТ И СИНТЕЗ КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА

7.1 Расчет корректирующего устройства

Из рисунка 10 определили, что передаточная функция корректирующего устройства будет иметь вид:

(56)

При таком виде ЛАЧХ КУ по справочнику находим вид КУ. Получаем, что при таком виде ЛАЧХ параллельного корректирующего устройства, желаемую передаточную функцию корректирующего звена (56) можно реализовать по следующей схеме представленной на рисунке 11 [11].

Рисунок 11 – Cхема последовательного корректирующего устройства

Передаточная функция корректирующего устройства:

, (57)

где T₁=R₂∙C₂= 15,152; (58)

T₂==0.068. (59)

Задаемся значением С₁=10 мкФ. Тогда R₁=15 МОм, а R₂=1,2МОм.

В результате включения последовательного корректирующего устройства структурная схема системы автоматического отбеливания примет вид рисунка 12.

Рисунок 12 – Последовательное включение корректирующего устройства