4 Расчет динамических характеристик

Для построения ЛАЧХ не скорректированного привода системы необходимо определить частоту излома w₁.

(37)

Ордината точки пересечения ЛАЧХ с осью L(w) определяется следующим выражением:

20lg()=20lg(49,875)=33,958(38)

Таким образом, через точку (0; 34) до частоты сопряжения w_ср с наклоном – 20 дб/дек проводится прямая. Сопрягающаяся с ней прямая имеет наклон – 40 дб/дек.

Координата рабочей точки в логарифмической системе запишется

РТ (lg(_р); 20lg () ).

Рабочая частота запишется в виде:

, (39)

где _н – ускорение нагрузки, рад/с².

с^-1

lg(_р) = lg(1,714) =0,234 (40)

Требуемый угол качания ₀ определяется:

(41)

; (42)

Координата рабочей точки примет вид: РТ (1,714; 29,3).

Для обеспечения требуемой точности, ЛАЧХ нескорректированного привода должна пройти либо через рабочую точку, либо выше ее. Желаемую ЛАЧХ, определяющую требуемые динамические характеристики, построим по заданному коэффициенту колебательности M = 1.4

Определим границы среднечастотной асимптоты желаемой ЛАЧХ:

(43)

(44)

Затем, через РТ проведем линию (-40дБ/дек) до пересечения с , потом проводим линию (-20дБ/дек) до пересечения с, затем линия продолжается с наклоном (-40дБ/дек).

Совмещаем ЛАЧХ нескорректированного привода и желаемую. Для этого переносим желаемой ЛАЧХ параллельно самой себе до пересечения высокочастотных асимптот ЛАЧХ нескорректированного привода и желаемой.

Рисунок 7- ЛАЧХ, ЖЛАЧХ

О

пределим графически частоты ω₁ ,ω₂ ,ω₃

ω₂=0,9рад/с Т₁=(45)

ω₃=3,7 рад/с Т₂=(46)

ω₄=18 рад/с Т₄=(47)

По графику запишем функцию ЛАЧХ корректирующего звена :

(48)

По виду ЛАЧХ и передаточной функции находим корректирующее звено:

Рисунок 8 – Последовательное корректирующее звено

Рассчитаем параметры корректирующего звена:

Один из параметров зададим произвольно С₁=5мкФ

(49)

(50)

(51)

Тогда передаточная функция привода примет вид:

(52)

Определим истинный коэффициент усиления системы графически.

20lg=36 (53)

с^-1

Пересчитаем значение k_у, (54)

(55)

По полученной передаточной функции привода с последовательным корректирующим устройством построим ФЧХ привода – рисунок.

Рисунок 9- АЧХ и ФЧХ скорректированного привода

Из графика находим запас устойчивости по фазе и по амплитуде

• запас устойчивости по фазе составляет 40⁰;

• запас устойчивости по амплитуде максимально возможный, так как кривая ФЧХ не пересекает прямую -π.

По нормам запас устойчивости по фазе составляет 20…40⁰, по амплитуде 8..10дБ. Следовательно, данная система устойчива.

Рисунок 10 – Полная структурная схема привода с последовательной коррекцией

Оцениваем качество переходного процесса нескорректированного привода и привода с корректирующим устройством.

Качество оценивается по передаточной функции замкнутой системы. Передаточная функция нескорректированного привода выглядит следующим образом.

β δ α

α

Рисунок 11 – Передаточная функция нескорректированного привода

W(p)=

Wз(p)=(56)

Для построения графика переходного процесса в СУ найдем переходную характеристику h(t) с помощью Mathcad по формуле:

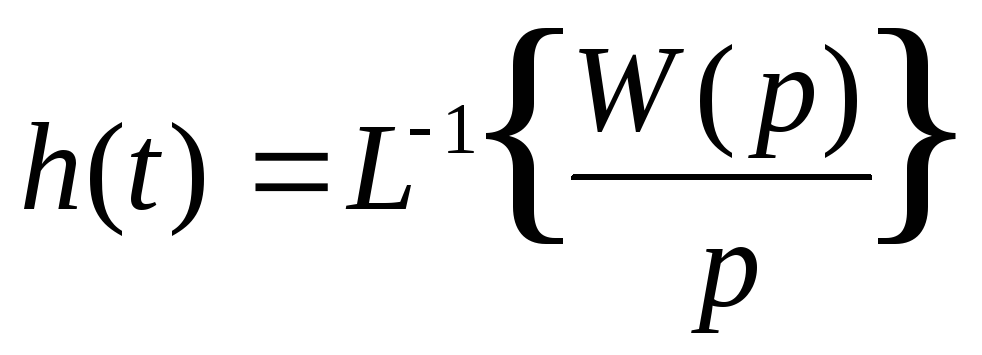, (57)

где L^-1 – обратное преобразование Лапласа,

p – комплексная переменная.

Получили, что h(t) имеет вид:

Рисунок 12- График переходного процесса h(t) нескорректированного

привода

По полученному переходному процессу определяем следующие показатели качества управления системы.

1. Установившееся значение h_уст= 1.

2. Время регулирования  = 5% (h_уст )=1*0,05 = 0,05;

t_p= 2,5 с.

3. Максимальное значение h_max=1,68

4. Время достижения максимума t_max= 0,18 с.

5. Время первого согласования t_1c=0.09

6. Перерегулирование σ(58)

W(p)

К(p)

β δ α

α

Рисунок 13 – Передаточная функция скорректированного привода

W(p)=

Передаточная функция корректирующего звена

Передаточная функция замкнутой системы имеет вид Wз(p)=

(59)

Для построения графика переходного процесса в СУ найдем переходную характеристику h(t) с помощью Mathcad по формуле:

,

где L^-1 – обратное преобразование Лапласа,

p – комплексная переменная.

Получили, что h(t) имеет вид:

График переходного процесса h(t) изображён на рисунке 14.

Рисунок 14- График переходного процесса скорректированного привода

По полученному переходному процессу определяем следующие показатели качества управления системы.

1. Установившееся значение h_уст= 1,02

2. Время регулирования  = 5% (h_уст )=1*0,05 = 0,051;

t_p= 1 с.

3. Максимальное значение h_max=1,35

4. Время достижения максимума t_max= 0,2 с.

5. Время первого согласования t_1c=0,1 с

Перерегулирование σ

ЗАКЛЮЧЕНИЕ

В ходе выполнения практической работы рассчитан следящий привод, удовлетворяющий ТЗ. Проведен анализ системы следящего привода с корректирующим устройством и без него. Анализ показывает, что корректирующее устройство улучшает устойчивость системы и делает ее более быстродействующей.