3 Подсчет передаточной функции системы

Составим передаточную функцию системы. Для этого нужно составить структурную схему:

Рисунок 4 – Структурная схема системы.

X– входной сигнал;

ИС – информационный сигнал с датчиков;

ЦИС – оцифрованный ИС;

Y – выходной сигнал системы.

Х – входной сигнал – импульс от частичного разряда поступает на датчики. На каждом датчике учитывается соответствующая составляющая. С датчиков сигналы через ФВЧ поступают на параллельные входы АЦП устройства PDPA. С АЦП сигналы поступают на сумматор и результирующая поступает на ЦП, который вырабатывает соответствующий сигнал сигнализации у.

Передаточная функ111111111111111111111111111111111111111111111111111111111111

11111111₁₁₁₁11₁₁₁₁₁₁11₁₁₁₁₁₁111111₁₁₁₁11₁₁₁₁₁₁11₁₁₁₁₁₁111111₁₁₁₁11₁₁₁₁₁₁11₁₁₁₁₁₁1111₁₁₁₁

111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111имеет вид:

(11);

для анализа передаточной функции необходимо перейти к псевдочастоте. Для этого полученную функцию на фиксатор нуля и заменим z на (1+)/(1-). Получим:

(12);

Далее заменим наjT₀/2, получим:

(13);

Далее проведем анализ устойчивости системы.

Для этого проведем построение АФЧХ системы.

График построен в MathCad 7:

Рисунок 5 – АФЧХ системы.

Так как график не огибает точку с координатами (-1;j0), то система устойчива.

4 Построение действительной логорифмической амплитудной частотной характеристики системы

Для построения необходимо разбить числитель и знаменатель на скобки.

При решении числителя и знаменателя относительно были получены следующие корни:

числитель:

₁=2,5610⁷+3,8610⁸j;

₂=-2,5610⁷+3,8610⁸j;

₃=4,2910⁸j;

₄=-210⁸j;

знаменатель:

₁=0;

₂=0;

₃=0;

₄=-410⁸j.

В результате получим:

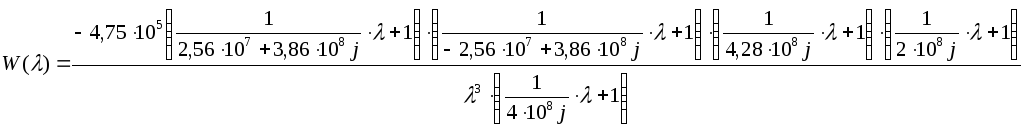(14).

Так как под логарифм при вычислении частот излома подставляются модули 1/Т, то можно их вычислить сразу:

(15);

(16);

(17);

(18);

(19).

Теперь рассчитаем частоты излома:

(20);

(21);

(22);

(23);

(24).

По полученным точкам строим ЛАЧХ.

5 Построение желаемой логорифмической амплитудной частотной характеристики системы

Исходные данные для построения ЖЛАЧХ получаем из технического задания и технических данных устройств системы:

М=1,13; g`=0,03;

t_p=0,01;g``=0,0027 – производная отg`.

E=0,0025;

По номограмме Солодовникова находим частоту среза:

t_p=4/_ср(25);

следовательно: _ср=4/t_p=1256 (26);

найдем координаты рабочей точки:

_к=g``/g`=0,09 (27);

A=g`/_к=0,33 (28);

A₁=A/E=132 (29);

Координаты точки В: (lg_к; 20lgA₁).

Строим точку В и проводим через нее –20дб/дек. Ниже этой линии находится запретная зона.

Находим h и граничные частоты ЖЛАЧХ:

h=(M+1)/(M-1)=16,4 (30);

₅=_cph (31);

(32);

lg/₅/=3,7 (33);

lg/₆/=2,5 (34);

В результате получим типовую ЖЛАЧХ. Совместим низкочастотные части действительной и типовой и получим фактическую ЛАЧХ.

Построим ее передаточную функцию:

(35).

Построим ЛФЧХ системы:

()=-90+arctan(T1)-arctan(T2)+2arctan(T3);

(0)=-90+arctan(310,150) -arctan(50861)+arctan(10⁹1)=-90;

(1)=-90+arctan(310,151) -arctan(50861)+arctan(10⁹1)=90;

(10)=-90+arctan(310,1510)-arctan(508610)+arctan(10⁹10)=90;

(100)=-90+arctan(310,15100)-arctan(5086100)+arctan(10⁹100)=90;

(1000)=-90+arctan(310,151000) -arctan(50861000)+arctan(10⁹1000)=90;

(1000)=-90+arctan(310,1510000) -arctan(508610000)+ arctan(10⁹10000)= =90.

Запас по фазе равен 9,42 радиан;

по амплитуде можно считать нормальным так как график ЛФЧХ не пересекает линию -2.