Черт. 87. Эпюра кривизны в железобетонном элементе с переменным по длине сечением

В формулах (293) и (294) кривизны определяются по формулам (269) и (292) соответственно для участков без трещин и с трещинами; знак принимается в соответствии с эпюрой кривизн.

При определении прогибов статически неопределимых конструкций рекомендуется учитывать перераспределение моментов, вызванных образованием трещин и неупругими деформациями бетона.

Для изгибаемых элементов постоянного сечения, имеющих трещины, на каждом участке, в пределах которого изгибающий момент не меняет знака, кривизну допускается вычислять для наиболее напряженного сечения, принимая ее для остальных сечений такого участка изменяющейся пропорционально значениям изгибающего момента (черт. 88).

Черт. 88. Эпюры изгибающих моментов и кривизны в железобетонном элементе постоянного сечения

а — схема расположения нагрузки; б — эпюра изгибающих моментов; в  эпюра кривизны

4.23 (4.32, 4.33). Для изгибаемых элементов при необходимо учитывать влияние поперечных сил на их прогиб. В этом случае полный прогиб f_tot равен сумме прогибов, обусловленных соответственно деформацией изгиба f_m и деформацией сдвига f_q.

Прогиб f_q, обусловленный деформацией сдвига, определяется по формуле 1

(295)

где  поперечная сила в сечении х от действия по направлению искомого перемещения единичной силы, приложенной в сечении, где определяется прогиб;

_x  деформация сдвига, определяемая по формуле

(296)

здесь Q_x  поперечная сила в сечении х от действия внешней нагрузки;

_b2  коэффициент, учитывающий влияние длительной ползучести бетона и принимаемый по табл. 31; при непродолжительном действии нагрузки _b2 = 1,0;

G — модуль сдвига бетона (см. п. 2.12);

_crc — коэффициент, учитывающий влияние трещин на деформации сдвига и принимаемый равным:

на участках по длине элемента, где

отсутствуют нормальные и наклонные

к продольной оси элемента трещины.................... 1,0;

на участках, где имеются только наклонные к

продольной оси элемента трещины....................... 4,8;

на участках, где имеются только нормальные или нормальные и наклонные к продольной оси элемента трещины, — по формуле

(297)

здесь M_x, — соответственно момент и кривизна в сечении от нагрузки, при которой определяется прогиб, при непродолжительном ее действии.

(4.34). Для сплошных плит толщиной менее 250 мм, армированных плоскими сетками, с трещинами в растянутой зоне значения прогибов, подсчитанные по формуле (293), умножаются на коэффициент , принимаемый не более 1,5, где h_o — в мм.

Определение продольных деформаций

4.25. Относительные деформации _o (удлинения или укорочения) в направлении продольной оси элементов определяются следующим образом.

1. Относительные деформации внецентренно сжатых и внецентренно растянутых элементов с однозначной эпюрой напряжений:

а) для внецентренно сжатых элементов или их отдельных участков — по формуле

(298)

б) для внецентренно растянутых элементов или их участков при отсутствии трещин — по формуле

(299)

В формулах (298) и (299) знак «плюс» соответствует деформациям укорочения, знак «минус» — деформациям удлинения;

в) для внецентренно растянутых элементов или их участков при наличии трещин (т. е. для элементов, указанных в п. 4.18), — по формуле

(300)

где _sm, _sm — средние величины удлинения арматуры соответственно S и S', определяемые по формулам:

(301)

здесь z_s, _s, _s  см. п. 4.18.

2. Относительные деформации изгибаемых, внецентренно сжатых и внецентренно растянутых элементов с двухзначной эпюрой напряжений в сечении:

а) для элементов или их отдельных участков, не имеющих трещин в растянутой зоне, — по формуле

. (302)

Правило знаков то же, что для формул (298) и (299);

б) для участков элементов, указанных в п. 4.15, имеющих трещины в растянутой зоне, — по формуле

(303)

где _sm, _bm — средние величины соответственно относительного удлинения арматуры и относительного укорочения крайнего сжатого волокна бетона на участке между трещинами, определяемые по формулам:

(304)

(305)

где M_s, _s, z, _f,   см. пп. 4.15 — 4.17; правило знаков — см. п. 4.15;

в) для участков внецентренно растянутых элементов, указанных в п. 4.19, — линейной интерполяцией между значением _о, определенным по формуле (300) при е_s = 0 (т. е. при е_o = y_so), и значением е_o, определенным по формуле (303) при е_s = 0,8h_o (т. е. при при е_o = 0,8 h_o + y_so), где y_so  см. п. 4.19.

В формулах (298)  (305):

y_s — расстояние от рассматриваемого волокна до центра тяжести арматуры S;

у_о — то же, до центра тяжести приведенного сечения;

_b1, _b2 — см. п. 4.14; при непродолжительном действии нагрузки _b2 = 1,0;

v — см. п. 4.15.

Деформации _о, определенные по формулам (298) — (303), со знаком «плюс» отвечают укорочению, со знаком «минус» — удлинению.

При одновременном действии постоянных, длительных и кратковременных нагрузок порядок вычисления _о аналогичен определению полной кривизны по п. 4.21.

4.26. Укорочение (удлинение) элементов на уровне рассматриваемого волокна определяется по формуле

(306)

где _оi  относительные продольные деформации в сечении, расположенном посредине участка длиной l_i;

п — число участков, на которые разбивается длина элемента.

Приближенные методы расчета деформаций

4.27. Прогибы железобетонных изгибаемых элементов из тяжелого бетона постоянного сечения, эксплуатируемых при нормальной и повышенной влажности (влажность воздуха окружающей среды свыше 40 %), заведомо меньше предельно допустимых, если выполняется условие

(307)

где _lim — граничное отношение пролета к рабочей высоте сечения, менее которого проверка прогибов не требуется (табл. 33).

При прогибы заведомо меньше предельно допустимых, если выполняется условие (308), учитывающее влияние деформаций сдвига на прогиб элемента:

(308)

Значения _lim, приведенные в табл. 33, отвечают продолжительному действию равномерно распределенной нагрузки на свободно опертую балку при предельном прогибе, равном .

Таблица 33

Сечения	Коэффициенты f, ft	Значения lim для определения случаев, когда проверка прогибов элементов из тяжелого бетона не требуется, при значениях , равных
		0,02	0,04	0,07	0,10	0,15	0,20	0,30	0,40	0,50
	f = ft = 0	25 17	17 12	14 10	12 9	10 8	9 8	10 10	11 11	11 11
	f = 0,2; ft = 0	31 22	22 16	18 13	16 11	12 9	10 8	10 10	11 11	11 11
	f = 0,4; ft = 0	42 25	25 17	23 15	18 12	14 10	11 8	10 9	10 9	11 11
	f = 0,6; ft = 0	45 30	28 30	24 17	19 14	16 12	13 9	11 9	10 10	11 11
	f = 0,8; ft = 0	48 32	30 21	25 18	20 15	18 13	15 10	12 9	10 9	10 10
	f = 1,0; ft = 0	50 35	33 22	26 19	23 17	20 14	17 12	14 9	11 9	10 10
	ft = 0,2; f = 0	28 18	17 12	14 10	12 9	10 8	9 8	10 10	11 11	11 11
	ft = 0,6; f = 0	32 20	20 13	15 10	13 9	10 8	9 9	10 10	11 11	12 12
	ft = 1,0; f = 0	36 22	23 14	16 10	13 9	10 8	9 9	10 10	11 11	12 12
	f = ft = 0,2	34 23	25 17	19 14	16 11	12 9	10 8	10 10	11 11	11 11
	f = ft = 0,6	48 33	34 25	26 18	21 14	16 12	15 9	11 8	10 10	11 11
	f = ft = 1,0	55 42	44 36	36 21	26 17	20 14	17 12	14 9	11 9	10 9
As = As

Примечание. Значения _lim, приведенные над чертой, применяются при расчете элементов, армированных сталью класса А-II, под чертой  класса A-III.

Если предельно допустимые прогибы f (см. п. 1.17) меньше , значения _lim табл. 33 должны быть уменьшены в раз (например, при — в 1,5 раза, при — в 2 раза).

Для сплошных плит толщиной менее 250 мм, армированных плоскими сетками, значения _lim уменьшаются делением на коэффициент, указанный в п. 4.24.

Примечание. Значения _lim могут быть увеличены в следующих случаях:

а) если прогиб определяется от действия момента M_l, составляющего часть полного момента М_tot (поз. 2  4 табл. 2),  умножением _lim табл. 33 на отношение М_tot/ M_l;

б) если нагрузка отличается от равномерно распределенной  умножением значений _lim табл. 33 на отношение где р_m  коэффициент, принимаемый по табл. 35 в зависимости от схемы загружения;

в) если прогиб определяется от совместного действия кратковременных, длительных и постоянных нагрузок — умножением значений _lim табл. 33 на коэффициент _, определяемый по формуле

где   отношение деформации от длительного действия нагрузки к деформации от кратковременного действия той же нагрузки, принимаемое равным для элементов: прямоугольного сечения  = 1,8; таврового сечения с полкой в сжатой зоне  = 1,5; таврового сечения с полкой в растянутой зоне  = 2,2.

ОПРЕДЕЛЕНИЕ КРИВИЗНЫ

4.28. Для изгибаемых элементов из тяжелого бетона постоянного сечения, указанных в п. 4.15 и эксплуатируемых при влажности воздуха окружающей среды свыше 40 %, кривизна на участках с трещинами определяется по формуле

(309)

где ₁, ₂ — см. табл. 34.

При одновременном действии постоянных, длительных и кратковременных нагрузок кривизна определяется по формуле

(310)

где _1sh — коэффициент ₁ при непродолжительном действии нагрузки;

_1l, _2l — коэффициенты ₁ и ₂ при продолжительном действии нагрузки.

ОПРЕДЕЛЕНИЕ ПРОГИБОВ

4.29. Для изгибаемых элементов при прогиб f определяется следующим образом:

а) для элементов постоянного сечения, работающих как свободно опертые или консольные балки,  по формуле

(311)

где  кривизна в сечении с наибольшим изгибающим моментом от нагрузки, при которой определяется прогиб;

р_m — коэффициент, принимаемый по табл. 35;

Таблица 34

Коэффициенты		Коэффициент 1 при значениях , равных																		Коэффициент 2 при значениях , равных
ft	f	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,10	0,13	0,15	0,17	0,20	0,25	0,30	0,35	0,40	0,45	0,50	<0,04	0,04-0,08	0,08-0,15	0,15-0,30	0,30-0,50
Продолжительное действие нагрузки
0,0 0,0 0,0 0,0 0,0 0,0	0,0 0,2 0,4 0,6 0,8 1,0	0,43 0,49 0,52 0,54 0,56 0,57	0,39 0,46 0,49 0,51 0,53 0,54	0,36 0,44 0,47 0,49 0,51 0,52	0,34 0,42 0,46 0,48 0,49 0,51	0,32 0,41 0,45 0,47 0,48 0,50	0,30 0,39 0,44 0,46 0,47 0,49	0,28 0,37 0,42 0,44 0,46 0,48	0,26 0,35 0,40 0,43 0,45 0,47	0,23 0,31 0,38 0,42 0,44 0,46	0,22 0,29 0,35 0,39 0,42 0,44	0,21 0,27 0,33 0,37 0,40 0,42	0,19 0,25 0,31 0,35 0,38 0,41	0,16 0,21 0,26 0,31 0,35 0,38	0,14 0,19 0,24 0,28 0,32 0,35	0,13 0,17 0,22 0,25 0,29 0,32	0,12 0,16 0,20 0,23 0,27 0,30	0,11 0,14 0,18 0,22 0,25 0,28	0,10 0,13 0,17 0,20 0,23 0,26	0,10 0,12 0,13 0,13 0,14 0,15	0,07 0,09 0,10 0,11 0,12 0,13	0,04 0,05 0,06 0,08 0,09 0,10	0,00 0,00 0,02 0,02 0,04 0,06	0,00 0,00 0,00 0,00 0,00 0,00
0,2 0,4 0,6 0,8 1,0	0,0 0,0 0,0 0,0 0,0	0,47 - - - -	0,40 0,42 0,43 - -	0,36 0,36 0,37 0,38 0,40	0,33 0,33 0,33 0,33 0;33	0,31 0,31 0,31 0,30 0,30	0,30 0,30 0,30 0,29 0,29	0,28 0,28 0,27 0,27 0,27	0,26 0,26 0,25 0,24 0,24	0,23 0,22 0,22 0,22 0,22	0,22 0,21 0,21 0,21 0,20	0,21 0,20 0,20 0,20 0,19	0,19 0,19 0,18 0,17 0,17	0,16 0,16 0,15 0,15 0,15	0,14 0,14 0,14 0,14 0,14	0,13 0,13 0,12 0,12 0,12	0,11 0,11 0,11 0,11 0,11	0,11 0,10 0,10 0,10 0,10	0,10 0,10 0,10 0,10 0,10	0,15 0,18 0,20 0,23 0,25	0,12 0,16 0,19 0,22 0,24	0,08 0,13 0,17 0,20 0,23	0,03 0,06 0,09 0,12 0,14	0,00 0,02 0,03 0,05 0,06
0,2 0,4 0,6 0,8 1,0	0,2 0,4 0,6 0,8 1,0	0,51 - - - -	0,45 0,53 - - -	0,43 0,49 0,53 - -	0,40 0,47 0,50 0,53 0,61	0,38 0,45 0,48 0,50 0,53	0,37 0,43 0,46 0,48 0,50	0,36 0,42 0,44 0,46 0,48	0,34 0,39 0,41 0,44 0,45	0,30 0,37 0,39 0,41 0,43	0,28 0,35 0,38 0,39 0,40	0,26 0,33 0,36 0,38 0,39	0,24 0,30 0,34 0,37 0,38	0,21 0,26 0,31 0,34 0,36	0,19 0,23 0,28 0,31 0,34	0,17 0,21 0,25 0,29 0,32	0,16 0,20 0,23 0,26 0,29	0,14 0,18 0,21 0,25 0,27	0,13 0,17 0,20 0,23 0,26	0,16 0,20 0,24 - -	0,13 0,19 0,22 0,25 0,26	0,08 0,14 0,20 0,24 0,25	0,04 0,07 0,12 0,19 0,20	0,00 0,03 0,04 0,08 0,12
Непродолжительное действие нагрузки
0,0 0,0 0,0 0,0 0,0 0,0	0,0 0,2 0,4 0,6 0,8 1,0	0,64 0,72 0,76 0,79 0,82 0,84	0,59 0,66 0,69 0,71 0,73 0,74	0,56 0,63 0,66 0,69 0,70 0,71	0,53 0,61 0,65 0,67 0,68 0,69	0,51 0,59 0,63 0,65 0,67 0,68	0,50 0,58 0,62 0,64 0,66 0,67	0,49 0,57 0,61 0,63 0,65 0,66	0,46 0,56 0,60 0,63 0,65 0,66	0,43 0,53 0,59 0,62 0,64 0,66	0,41 0,51 0,57 0,61 0,63 0,65	0,40 0,49 0,56 0,60 0,63 0,65	0,37 0,46 0,53 0,58 0,61 0,63	0,34 0,43 0,49 0,55 0,58 0,61	0,32 0,40 0,46 0,52 0,56 0,59	0,30 0,37 0,44 0,49 0,53 0,56	0,28 0,35 0,41 0,46 0,50 0,54	0,26 0,33 0,39 0,44 0,48 0,52	0,25 0,31 0,37 0,42 0,46 0,50	0,17 0,21 0,23 0,25 0,26 0,27	0,14 0,18 0,20 0,21 0,23 0,24	0,09 0,11 0,14 0,16 0,17 0,18,	0,02 0,03 0,04 0,05 0,06 0,07	0,00 0,00 0,00 0,00 0,00 0,00
0,2 0,4 0,6 0,8 1,0	0,0 0,0 0,0 0,0 0,0	0,74 - - - -	0,60 0,63 0,81 - -	0,56 0,57 0,59 0,63 0,84	0,53 0,54 0,54 0,55 0,57	0,51 0,51 0,51 0,51 0,52	0,49 0,49 0,49 0,49 0,49	0,47 0,47 0,47 0,47 0,47	0,44 0,44 0,44 0,44 0,44	0,42 0,42 0,42 0,42 0,42	0,40 0,40 0,40 0,40 0,40	0,39 0,39 0,39 0,39 0,39	0,37 0,37 0,37 0,37 0,37	0,34 0,34 0,34 0,34 0,34	0,32 0,32 0,32 0,32 0,32	0,30 0,30 0,30 0,30 0,30	0,28 0,28 0,28 0,28 0,28	0,26 0,26 0,26 0,26 0,27	0,25 0,25 0,25 0,25 0,25	0,28 0,35 0,36 0,45 0,50	0,23 0,31 0,39 0,40 0,46	0,16 0,25 0,32 0,38 0,44	0,07 0,14 0,20 0,25 0,29	0,00 0,03 0,08 0,12 0,15
0,2 0,4 0,6 0,8 1,0	0,2 0,4 0,6 0,8 1,0	0,79 - - - -	0,67 0,77 - - -	0,63 0,69 0,76 - -	0,61 0,66 0,70 0,76 0,92	0,59 0,64 0,67 0,71 0,76	0,58 0,62 0,65 0,68 0,71	0,56 0,61 0,64 0,66 0,69	0,55 0,58 0,61 0,64 0,66	0,52 0,56 0,58 0,61 0,63	0,50 0,55 0,57 0,59 0,61	0,48 0,54 0,56 0,58 0,60	0,46 0,52 0,55 0,57 0,58	0,42 0,48 0,53 0,56 0,57	0,39 0,45 0,50 0,53 0,56	0,37 0,43 0,47 0,51 0,54	0,35 0,40 0,45 0,49 0,52	0,33 0,38 0,43 0,47 0,50	0,31 0,37 0,41 0,45 0,48	0,27 0,39 0,50 - -	0,24 0,37 0,46 0,60 0,72	0,17 0,30 0,44 0,57 0,70	0,08 0,16 0,28 0,41 0,55	0,00 0,04 0,11 0,21 0,31

при схеме загружения свободно опертой или консольной балки, не приведенной в табл. 35, прогиб определяется по формулам сопротивления материалов при жесткости, равной отношению наибольшего момента к наибольшей кривизне;

б) если прогиб, определенный по подпункту «а», превышает допустимый, то для слабоармированных элементов (  0,5 %) его значение рекомендуется уточнять за счет учета повышенной жесткости на участках без трещин при переменной жесткости на участке с трещинами; для свободно опертых балок, загруженных равномерно распределенной нагрузкой, это соответствует формуле

(312)

где р_crc — коэффициент, принимаемый по табл. 36 в зависимости от отношения M_crc/M_tot (M_crc  см. пп. 4.2 и 4.3) ;

— кривизна в сечении с наибольшим моментом, определенная как для сплошного тела по формуле (270), от нагрузки, при которой определяется прогиб; допускается значение I_red в формуле (270) определять как для бетонного элемента.

Для иных схем загружения величина f может быть определена по формуле (314) ;

в) для изгибаемых элементов с защемленными опорами прогиб в середине пролета определяется по формуле

(313)

где — кривизны элемента соответственно в середине пролета, на левой и правой опорах;

р_m  коэффициент, определяемый по табл. 35 как для свободно опертой балки;

г) для элементов переменного сечения, а также в тех случаях, когда требуется более точное, чем по формулам (311) и (313), определение прогибов, а сами элементы и нагрузка симметричны относительно середины пролета, прогиб определяется по формуле

Таблица 35

Схема загружения консольной балки	Коэффициент рm	Схема загружения свободно опертой балки	Коэффициент рm

Примечание. При загружении элемента одновременно по нескольким схемам (где p_m1 и M₁, p_m2 и M₂ и т. д.  соответственно коэффициент p_m, и наибольший изгибающий момент М для каждой схемы загружения). В этом случае в формулах (311)  (313) величина определяется при значении М, равном сумме наибольших изгибающих моментов, определенных для каждой схемы загружения.

Таблица 36

Mcrc/Mtot	1,00	0,99	0,98	0,96	0,94	0,92	0,90	0,85	0,80
Pcrc	0,104	0,088	0,082	0,073	0,067	0,062	0,058	0,049	0,042

Продолжение табл. 36

Mcrc/Mtot	0,75	0,70	0,60	0,50	0,40	0,30	0,20	0,10	0,00
Pcrc	0,036	0,032	0,024	0,018	0,013	0,008	0,005	0,002	0,000

где

(314)

где — кривизны соответственно на опоре, на расстоянии от опоры, на расстоянии от опоры и в середине пролета; значения кривизн подсчитываются со своими знаками согласно эпюре кривизн.

В остальных случаях прогиб в середине пролета рекомендуется определять по формуле (294).

Входящие в формулы (311)  (314) значения кривизн определяются по формулам (271), (272), (282), (286), (309) и (310) при наличии трещин в растянутой зоне и по формулам (269) и (270) — при их отсутствии.

Для сплошных плит толщиной менее 250 мм необходимо учитывать указания п. 4.24.

4.30. Для коротких элементов (l/h < 10) постоянного сечения, работающих как свободно опертые балки, прогиб вычисляется согласно п. 4.29 и умножается на коэффициент P_q, учитывающий влияние деформаций сдвига. Коэффициент P_q определяется по формуле

(315)

где _q = 0,5 — при отсутствии как нормальных, так и наклонных трещин, т.е. при выполнении условий (233) и (248);

_q = 1,5 — при наличии нормальных или наклонных трещин;

р_m — см. табл. 35.

Примеры расчета

Пример 57. Дано: железобетонная плита перекрытия гражданского здания прямоугольного сечения размерами h = 120 мм, b = 1000 мм, h_o = 105 мм; пролет l = 3,1 м; бетон тяжелый класса В25 (E_b =2,710⁴ МПа; R_bt.ser = 1,6 МПа); растянутая арматура класса А-II (Е_s = 2,110⁵ МПа), площадь ее поперечного сечения А_s = 393 мм² (5 10); полная равномерно распределенная нагрузка q_tot = 7 кН/м, в том числе ее часть от постоянных и длительных нагрузок q_l = 6 кН/м; прогиб ограничивается эстетическими требованиями.

Требуется рассчитать плиту по деформациям.

Расчет. Определим необходимость расчета плиты по деформациям согласно п. 4.27:

Из табл. 33 по  = 0,029 и _f = _ft = 0 находим _lim = 21. Так как h < 250 мм, то _lim корректируем путем деления на коэффициент Тогда

Учитывая примечание к п. 4.27 (случай «а»), имеем

Поскольку - расчет по деформациям необходим.

Определим кривизну в середине пролета от действия момента М_l (так как прогиб ограничивается эстетическими требованиями).

Принимаем без расчета, что элемент имеет трещины в растянутой зоне, в связи с чем кривизну определим по формуле (309).

Из табл. 34 по  = 0,028 и _f = _ft = 0 находим значения ₁ = 0,393 и ₂ = 0,10, соответствующие продолжительному действию нагрузки.

Прогиб определим согласно п. 4.29а, принимая, согласно табл. 35, :

Так как h < 250 мм, полный прогиб равен f = 13,5  1,23 = 16,6 мм, что больше предельно допустимого прогиба (см. табл. 2).

Поскольку  = 0,00375 < 0,005, согласно п. 4.296 уточним значение f по формуле (312). Для этого вычислим величины и M_crc.

Так как рассчитывается слабоармированный элемент ( < 0,01), I_red и М_crc определим как для бетонного сечения (см. пп. 4.2 и 4.3):

_b1 = 0,85 (как для тяжелого бетона);

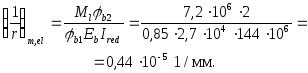
Коэффициент р_сrс определим по табл. 36 при

.

С учетом поправки на малую высоту сечения (h < 250 мм) f = 9,841,23 = 12,1 мм, что меньше предельно допустимого прогиба f = 15,5  мм.

Поскольку l/h > 10, влиянием деформаций сдвига пренебрегаем.

Пример 58: Дано: ригель перекрытия общественного здания прямоугольного сечения размерами b = 200 мм, h = 600 мм; a = 80 мм; пролет ригеля l = 4,8 м; бетон тяжелый класса В25 (Е_b = 2,7  10⁴ МПа; R_bt,ser = 1,6 МПа); рабочая арматура класса А-III (E_s = 2  10⁵ МПа), площадь ее поперечного сечения А_s = 2463 мм (4 28); полная равномерно распределенная нагрузка q_tot = 85,5 кН/м, в том числе ее часть от постоянных и длительных нагрузок q_l = 64 кН/м; прогиб ограничивается эстетическими требованиями; влажность воздуха в помещении свыше 40 %.

Требуется рассчитать ригель по деформациям.

Расчет. Определим необходимость расчета по деформациям согласно п. 4.27.

h_o = 600 ‑ 80 = 520 мм ;

Так как l/h = 4,8/0,6 = 8 < 10, необходимо учитывать влияние деформаций сдвига на прогиб элемента: l/h_o = 4,8/0,52 = 9,3. По табл. 33 при  = 0,176 и _f = _ft = 0 находим _lim = 8.

т. е. расчет по деформациям необходим.

Поскольку  = 0,238 > 0,005, согласно п. 4.1 кривизну определим с учетом наличия трещин в растянутой зоне. Так как прогиб ограничивается эстетическими требованиями, расчет производим на действие момента М_l. Кривизну в середине пролета вычислим по формуле (309).

По табл. 34 при  = 0,176 и _f = _ft = 0 находим ₁ = 0,206 и ₂ = 0.

Полный прогиб определим согласно пп. 4.29а и 4.30 с учетом влияния деформаций сдвига. Согласно табл. 35,

т. е. прогиб ригеля меньше предельно допустимого (см. табл. 2).

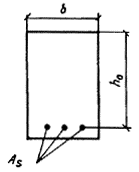
Пример 59. Дано: железобетонная плита покрытия с расчетным пролетом 5,7 м; размеры поперечного сечения (для половины сечения плиты) — по черт. 89; бетон легкий класса В25 (R_b,ser = 18,5 МПа; R_bt,ser = 1,6 МПа), марки по средней плотности D1600 (E_b =16,510³ МПа); рабочая арматура класса А-II (E_s = 2,110⁵ МПа), площадь ее сечения A_s = 380 мм² (122); постоянная и длительная равномерно распределенные нагрузки на плиту q_l = 8,75 кН/м; прогиб плиты ограничивается эстетическими требованиями; помещение, перекрываемое плитой, имеет нормальную влажность воздуха (40  75 %).

Требуется рассчитать плиту по деформациям.