
- •Пособие по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры (к сНиП 2.03.01-84)
- •Предисловие
- •1. Общие рекомендации основные положения
- •Основные расчетные требования
- •2. Материалы для бетонных и железобетонных конструкций бетон
- •Арматура
- •Нормативные и расчетные характеристики арматуры
- •3. Расчет бетонных и железобетонных элементов по предельным состояниям первой группы
- •Расчет бетонных элементов по прочности
- •Внецентренно сжатые элементы
- •Черт. 1. Схема усилий к эпюра напряжении в поперечном сечении внецентренно сжатого бетонного элемента без учета сопротивления бетона растянутой зоны
- •Черт. 2. К определению Ab1
- •Черт. 3. График несущей способности внецентренно сжатых бетонных элементов Изгибаемые элементы
- •Примеры расчета
- •Расчет железобетонных элементов по прочности
- •Изгибаемые элементы
- •Примеры расчета
- •Элементы, работающие на косой изгиб
- •Черт. 33. Сжатые элементы с косвенным армированием
- •Черт. 34. Схема усилий в поперечном прямоугольном сечении внецентренно сжатого элемента
- •Черт. 35. Графики несущей способности внецентренно сжатых элементов прямоугольного сечения с симметричной арматурой
- •Черт. 36. Схема, принимаемая при расчете внецентренно сжатого элемента прямоугольного сечения с арматурой, расположенной по высоте сечения
- •Прямоугольные сечения с несимметричной арматурой
- •Черт. 46. К примеру расчета 28
- •Черт. 47. К примеру расчета 29
- •Черт. 48. К примеру расчета 32
- •Черт. 49. К примерам расчета 33, 34 и 39
- •Черт. 50. К примерам расчета 38 и 40
- •I граница сжатой зоны в первом приближении; II окончательная граница сжатой зоны
- •Черт. 51. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси внецентренно растянутого железобетонного элемента, при расчете его по прочности
- •Черт. 52. Схема усилий в пространственном сечении
- •Черт. 53. Схема усилий в пространственном сечении
- •Черт. 54. Определение изгибающего и крутящего моментов поперечной силы, действующих в пространственном сечении
- •Черт. 55. Расположение расчетных пространственных сечений
- •1, 2 Расчетные пространственные сечения;
- •Черт. 56. Разделение на прямоугольники сечений, имеющих входящие углы, при расчете на кручение с изгибом
- •Черт. 57. Схемы расположения сжатой зоны в пространственном сечении 1-й схемы железобетонного элемента двутаврового и таврового сечений, работающего на кручение с изгибом
- •Черт. 58. Схемы расположения сжатой зоны в пространственном сечении 2-й схемы железобетонного элемента двутаврового, таврового и г-образного сечений, работающего на кручение с изгибом
- •Черт. 59 Пространственное сечение железобетонного элемента кольцевого поперечного сечения, работающего на кручение с изгибом
- •Черт. 60. График для определения коэффициента при расчете элементов кольцевого поперечного сечения на кручение с изгибом
- •Черт. 61. К примеру расчета 46
- •Черт. 62. К примеру расчета 47
- •Черт. 63. Определение расчетной площади Aloc2 при расчете на местное сжатие при местной нагрузке
- •Черт. 64. К примеру расчета 48
- •Черт. 65. Схема пирамиды продавливания при угле наклона ее боковых граней к горизонтали
- •Черт. 66. Схема для определения длины зоны отрыва
- •Черт. 67. Армирование входящего угла, расположенного в растянутой зоне железобетонного элемента
- •Черт. 68. Расчетная схема для короткой консоли при действии поперечной силы
- •Черт. 69. Расчетная схема для короткой консоли при шарнирном опирании сборной балки, идущей вдоль вылета консоли
- •Черт. 70. К примеру расчета 49
- •Черт. 71. Схема усилий, действующих на закладную деталь
- •Черт. 72. Схема выкалывания бетона анкерами закладной детали с усилениями на концах при nan 0
- •1 Точка приложения нормальной силы n; 2 поверхность выкалывания; 3 — проекция поверхности выкалывания на плоскость, нормальную к анкерам
- •Черт. 73. Схема выкалывания бетона анкерами закладной детали без усилений на концах при n'an 0
- •1 Точка приложения нормальной силы n; 2 поверхность выкалывания; 3 проекция поверхности выкалывания на плоскость, нормальную к анкерам
- •Черт. 75. Конструкция закладной детали, не требующей расчета на выкалывание
- •Черт. 76. Схема для расчета на откалывание бетона нормальными анкерами закладной детали
- •Черт. 77. К примеру расчета 50
- •Черт. 78. К примеру расчета 51
- •Черт. 79. Незамоноличенный стык колонны
- •1 Центрирующая прокладка; 2 распределительный лист; 3 ванная сварка арматурных выпусков; 4 — сетки косвенного армирования торца колонны
- •Черт. 80. Расчетное сечение замоноличенного стыка колонны с сетками косвенного армирования в бетоне колонны и в бетоне замоноличивания
- •1 Бетон колонны; 2 бетон замоноличивания; 3 сетки косвенного армирования
- •Черт. 81. К примеру расчета 52
- •1 Арматурные выпуски; 2 — распределительный лист; 3 центрирующая прокладка
- •Черт. 82. Схема для расчета шпонок, передающих сдвигающие усилия от сборного элемента монолитному бетону
- •1 Сборный элемент; 2 монолитный бетон
- •Черт. 83. Схемы усилий и эпюры напряжений в поперечном сечении элемента при расчете его по образованию трещин, нормальных к продольной оси элемента
- •Черт. 84. Положение опорных реакций в жестких узлах, принимаемое для определения коэффициента loc
- •Черт. 85. Расчетные схемы для определения коэффициента loc
- •Черт. 86. К примеру расчета 53
- •Черт. 87. Эпюра кривизны в железобетонном элементе с переменным по длине сечением
- •Черт. 88. Эпюры изгибающих моментов и кривизны в железобетонном элементе постоянного сечения
- •Черт. 89. К примеру расчета 59
- •Черт. 130. Фиксаторы однократного использования, обеспечивающие требуемую толщину s защитного слоя бетона
- •Черт. 131. Фиксаторы однократного использования, обеспечивающие требуемое расстояние
- •Черт. 132. Фиксаторы однократного использования, обеспечивающие одновременно требуемые толщину защитного слоя бетона и расстояние между отдельными арматурными элементами
- •Усилия от внешних нагрузок и воздействий в поперечном сечении элемента
- •Характеристики материалов
- •Характеристика положения продольной арматуры в поперечном сечении элемента
- •Геометрические характеристики
Черт. 49. К примерам расчета 33, 34 и 39
Расчет в плоскости изгиба. Принимаем расчетную толщину полки равной средней высоте свесов hf = hf = 200 + 30/2 = 215 мм.
Вычислим площадь и момент инерции бетонного сечения:
![]() мм2;
мм2;

Радиус инерции сечения
![]() мм.
мм.
Так как l0/i = 16 200/520 = 31,1 < 35 и l0/i > 14, расчет производим с учетом прогиба элемента согласно п. 3.54, принимая значение Ncr равным:

Коэффициент определим по формуле (91):

Центр тяжести площади арматуры As
и As
отстоит от ближайшей грани
на расстоянии а = а
=
![]() мм, откуда h0
= h –
a = 1500 –
79 = 1421 мм.
мм, откуда h0
= h –
a = 1500 –
79 = 1421 мм.
Значение е с учетом прогиба элемента равно:
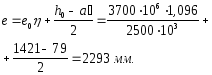
Проверим условие (130):
![]()
т. е. расчет производим как для двутаврового сечения.
Площадь сжатых свесов полки равна:
![]() мм2.
мм2.
Определим высоту сжатой зоны:
![]() мм.
мм.
Из табл. 18 находим R = 0,523. Так как х = 228 мм < R h0 = 0,523 · 1421 = 743 мм, прочность сечения проверим из условия (131):

т. е. прочность сечения в плоскости изгиба обеспечена.
Расчет из плоскости изгиба. Определим радиус инерции сечения из плоскости изгиба:
![]() мм4;
мм4;
![]() мм.
мм.
Так как гибкость из плоскости изгиба l0/i = 10 800/134 = 80 значительно превышает гибкость в плоскости изгиба l0/i = 31,1, согласно п. 3.51 проверим прочность сечения из плоскости изгиба, принимая эксцентриситет е0 равным случайному эксцентриситету еа. Высота сечения при этом равна h = 600 мм.
Поскольку случайный эксцентриситет,
согласно п. 3.50, еа =
![]() мм
мм
![]() мм, принимаем еа =
мм, принимаем еа =
![]() что при
что при
![]() позволяет производить расчет, согласно
п. 3.64, как для прямоугольного сечения,
не учитывая в „запас”
сечение ребра, т. е. принимая b
= 2 ·
215 = 430 мм.
позволяет производить расчет, согласно
п. 3.64, как для прямоугольного сечения,
не учитывая в „запас”
сечение ребра, т. е. принимая b
= 2 ·
215 = 430 мм.
Площадь сечения промежуточных стержней, расположенных вдоль обеих полок, равна As,int = 4826 мм2 (6 32), а площадь сечения всех стержней As,tot = 11 260 мм2 (14 32). Поскольку As,tot/3 = 11 260/3 = 3750 мм2 < As,int = 4826 мм2, в расчете используем табл. 27 (разд. Б). Из табл. 27 для тяжелого бетона при Nl/N = 2000/2500 = 0,8 и l0/h = 10,8/0,6 = 18 находим sb = 0,724.
Значение
![]() Следовательно,
= sb
= 0,724.
Следовательно,
= sb
= 0,724.
Проверим условие (119):
![]()
т. е. прочность сечения из плоскости изгиба обеспечена.
Пример 34. Дано: размеры сечения и расположения арматуры по черт. 49; бетон тяжелый класса В30 (Rb = 19 МПа при b2 = 1,1; Eb = 2,9 · 104 МПа); арматура симметричная класса A-III (Rs = Rsc = 365 МПа); продольная сила N = 6000 кН; изгибающий момент М = 3100 кН·м; расчетная длина элемента: в плоскости изгиба l0 = 16,2 м, из плоскости изгиба l0 = 10,8 м.
Требуется определить площадь сечения арматуры.
Расчет в плоскости изгиба. Из примера 33 имеем: hf = 15 мм; h0 =1421 мм; а = 79 мм; Ncr = 28 270 кН.
По формуле (91) определим коэффициент :

Значение е с учетом прогиба элемента равно:

Проверим условие (130):
![]()
т. е. расчет производим как для двутаврового сечения.
Площадь сжатых свесов полки равна:
![]() мм2.
мм2.
Определим значения n, m1, ov, m,ov, :
![]()
![]()
![]()

![]()
Из табл. 18 находим R = 0,523.
Так как = n
–
ov
= 1,111 –
0,302 = 0,809 > R
= 0,523, площадь арматуры определим по
формуле (135). Для этого по формулам (136) и
(132) вычислим значения s
и
![]()

Из табл. 18 находим с = 3,0 и = 0,698.


отсюда
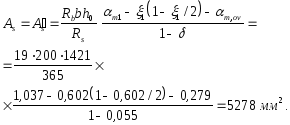
Принимаем As = As = 5630 мм2 (7 32).
Расчет из плоскости изгиба производим аналогично примеру 33.
КОЛЬЦЕВЫЕ СЕЧЕНИЯ
Пример 35. Дано: сечение с внутренним радиусом r1 = 150 мм, наружным r2 = 250 мм; бетон тяжелый класса В25 (Rb = 16 МПа при b2 = 1,1); продольная арматура класса A-III (Rs = Rsc = 365 МПа); площадь ее сечения As,tot = 1470 мм2 (13 12); продольная сила от полной нагрузки N = 1200 кН, ее эксцентриситет относительно центра тяжести сечения с учетом прогиба элемента равен е0 = 120 мм.
Требуется проверить прочность сечения.
Расчет. Вычислим площадь кольцевого сечения:
![]() мм2
мм2
Относительная площадь сжатой зоны бетона равна:

![]() мм.
мм.
Так как 0,15 < cir = 0,502 < 0,6, прочность сечения проверим из условия (138):

т. е. прочность сечения обеспечена.
КРУГЛЫЕ СЕЧЕНИЯ
Пример 36. Дано: сечение диаметром D = 400 мм; а = 35 мм; бетон тяжелый класса В25 (Rb = 13 МПа при b2 = 0,9; Eb = 2,7 · 104 МПа); продольная арматура класса A-III (Rs =Rsc = 365 МПа; Es = 2 · 105 МПа); площадь ее сечения As,tot = 3140 мм2 (10 20); продольные силы и изгибающие моменты: от постоянных и длительных нагрузок Nl = 400 кН·м; от всех нагрузок N = 600 кН, М = 140 кН·м; расчетная длина элемента l0 = 4 м.
Требуется проверить прочность сечения.
Расчет. Вычислим:
площадь круглого сечения
![]() мм2;
мм2;
радиус инерции сечения
![]() мм;
мм;
гибкость элемента
![]()
Следовательно, расчет производим с учетом влияния прогиба элемента согласно п. 3.54, а значение Ncr определим по формуле (92). Для этого вычислим:
![]() мм;
мм;

[здесь = 1,0 (см. табл. 16)];
![]()
Так как
![]() 0,583
> e,min
= 0,5 – 0,01 l0/D
–
0,01 Rb,
принимаем e
= e0/D
= 0,583.
0,583
> e,min
= 0,5 – 0,01 l0/D
–
0,01 Rb,
принимаем e
= e0/D
= 0,583.
Моменты инерции бетонного сечения и всей арматуры соответственно равны:
![]() мм4;
мм4;
![]() мм4;
мм4;
![]()
Тогда

Коэффициент определим по формуле (91):

Прочность сечения проверим с помощью графика черт. 41.
По значениям
![]()
![]() 0,702
и
0,702
и
![]() на графике находим m
= 0,51.
на графике находим m
= 0,51.
Поскольку mRbAr = 0,51 · 13 · 125 600 · 200 = 167 · 106 Н·мм = 167 кН·м > Ne = 600 · 0,233 · 1,12 = 156,6 кН·м, прочность сечения обеспечена.
Пример 37. По данным примера 36 необходимо подобрать продольную арматуру, пользуясь графиком черт. 41.
Расчет. Из примера 36 i = 100 мм, А = 125 600 мм2, rs = 165 мм. Поскольку l0/i = 4000/100 40 > 35, арматуру подбираем с учетом влияния прогиба элемента, вычисляя значение Ncr по формуле (92).
В первом приближении принимаем As,tot = 0,01 A = 1256 мм2, откуда
![]() мм4.
мм4.
Из примера 36 l = 1,695, e = 0,583, I = 1256 · 106 мм4.
Тогда

Значение коэффициента

По значениям
![]()
![]() находим s
= 0,74, откуда
находим s
= 0,74, откуда
![]() мм2.
мм2.
Поскольку полученное армирование существенно превышает принятое в первом приближении (As,tot = 1256 мм2), значение As,tot = 3310 мм2 определено с „запасом”, и его можно несколько уменьшить, уточнив значение Ncr.
Принимаем
![]() мм2 и производим аналогичный
расчет:
мм2 и производим аналогичный
расчет:
![]() мм4;
мм4;
![]() кН;
кН;

По значениям
![]() n
= 0,367 и
n
= 0,367 и
![]() на графике черт. 41 находим s
= 0,68.
на графике черт. 41 находим s
= 0,68.
![]() мм2.
мм2.
Принимаем As,tot = 3142 мм2 (10 20).
ЭЛЕМЕНТЫ, РАБОТАЮЩИЕ НА КОСОЕ ВНЕЦЕНТРЕННОЕ СЖАТИЕ
Пример 38. Дано: прямоугольное сечение колонны размерами b = 400 мм, h = 600 мм; бетон тяжелый класса В25 (Rb = 16 МПа при b2 = 1,1); продольная арматура класса A-III (Rs = Rsc = 365 МПа) расположена в сечении согласно черт. 50; в сечении одновременно действуют продольная сила N = 2600 кН и изгибающие моменты: в плоскости, параллельной размеру h, – Mx = 240 кН·м и в плоскости, параллельной размеру b, – My = 182,5 кН·м; моменты Мх и Мy даны с учетом прогиба колонны.
Требуется проверить прочность сечения.

