
1.4 Структурная схема системы автоматического регулирования
расхода сыпучих материалов
На основании полученных расчетов, формул (2),(4),(6),(13),(14) составляем структурную схему, внутри звеньев которой запишем полученные передаточные функции.
![]()




![]()



W1=1![]()





![]()



Рисунок 2 – Структурная схема САР сыпучих материалов

2 РАСЧЁТ ПЕРЕДАТОЧНОЙ ФУНКЦИИ СИСТЕМЫ АВТОМАТИЧЕС
КОГО РЕГУЛИРОВАНИЯ СЫПУЧИХ МАТЕРИАЛОВ
П![]() ередаточную
функцию всей системы получим путем
перемножения передаточных функций
последовательных звеньев системы и
сложения параллельных звеньев.
ередаточную
функцию всей системы получим путем
перемножения передаточных функций
последовательных звеньев системы и
сложения параллельных звеньев.
Подставим значения в формулу (15)
П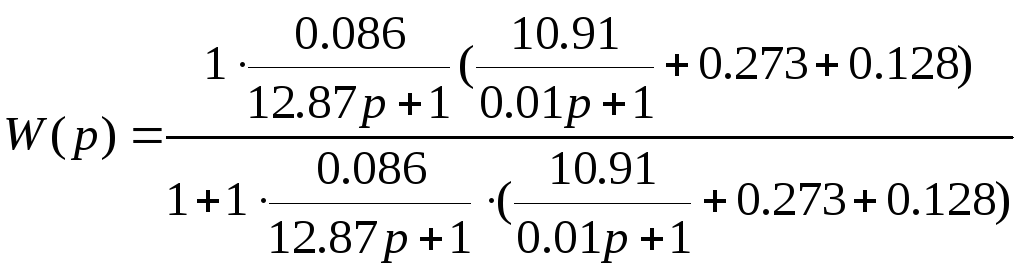 роизведя
математические операции в итоге получаем
передаточную функцию:
роизведя
математические операции в итоге получаем
передаточную функцию:
![]()
3 Определение устойчивости системы
Определим устойчивость системы по критерию Гурвица.
Критерий устойчивости Гурвица сформулирован в форме определителя, все элементы которого являются коэффициенты харрактерестического уравнения системы. При этом по главной диагонали располагают все коэффициенты от а1 и кончая аn. Каждый столбец вверх дополняется коэффициентом с возрастающими индексами, а вниз с убывающими.
Если индекс коэффициента больше n, но меньше нуля, то в данном месте проставляется ноль. Необходимые условия для критерия аn>0, достаточное условие – все определители Гурвица должны быть положительны.
Разрабатываемая система автоматического регулирования сыпучих материалов имеет характеристическое уравнение 6.5p+1=0
По характеристическому уравнению составим основной определитель Гурвица.
1 = | а1| = 6.5>0
Вывод: Необходимое условие устойчивости выполняется а0 >0, a1>0. Достаточное условие 1 = 6.5>0 не добавляет ограничения на коэффициенты. Следовательно систему можно считать устойчивой.
Так как разрабатываемая система является дискретной, необходимо провести z- преобразование
Проведём z-преобразование, учитывая дискретность Т0=32·10-6
Z-преобразование, проводится по формуле из таблице [5].
П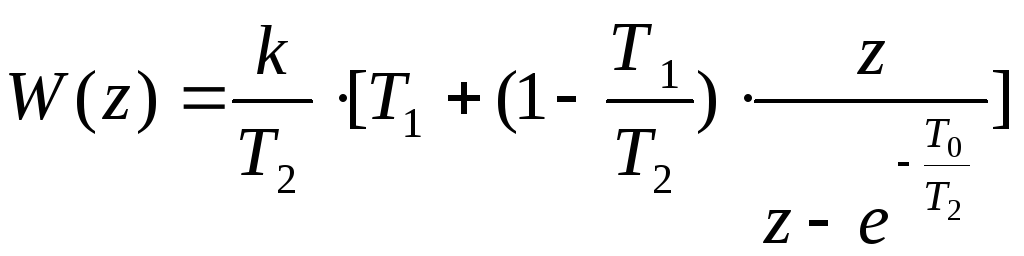 одставляем
числовые коэффициенты, получаем
следующее:
одставляем
числовые коэффициенты, получаем
следующее:
![]()
![]() Проведя
математические операции получаем:
Проведя
математические операции получаем:

Определим устойчивость системы по критерию Шур-Кона.
Так как харрактерестическое уравнение первого порядка, то записывается первый определитель
![]()
П![]() одставляем
числовые значения и проводим математические
операции получаем
одставляем
числовые значения и проводим математические
операции получаем
Вывод: система устойчива, так как нечётный определитель отрицателен.

