2. Инвариантность формы дифференциала

I. Пусть z=f(x,y), где x, y – независимые переменные, определена в области G. Пусть на G функция f имеет непрерывные частные производные. Тогда она дифференцируема и её дифференциал

, (1)

где , т.е. dx, dy – произвольные числа не зависящие от x и y.

II. Пусть теперь z является сложной функцией от переменных u и v, т.е. z=f(x,y), , . Независимые переменные u и v определены в области Н так, что . Тогда . Пусть на Н существуют непрерывные частные производные и на G - непрерывные частные производные и тогда существуют непрерывные частные производные и от сложной функции z=h(u,v):

, (2)

. (3)

Тогда сложная функция z=h(u,v) дифференцируема и её дифференциал

, (4)

du, dv – произвольные числа.

Подставляя (2) и (3) в (4), получим

.

Итак, , (5)

dx – дифференциал функции , ,

dy - дифференциал функции , .

Сравнив (1) и (5), можем сделать вывод. Дифференциал функции f имеет одну и ту же форму относительно x и y: , как в случае, когда x и y - независимые переменные, так и в случае, когда x и y – функции от других переменных. Это свойство называется инвариантностью формы полного дифференциала. Хотя форма (1) инвариантна (т.е. неизменна), но смысл символов dx и dy не один и тот же. Если x и y - независимые переменные, то dx и dy – числа, не зависящие от x, y. Если же x и y – функции, то dx и dy – дифференциалы этих функций.

Итак, так как форма (1) инвариантна, то полный дифференциал функции всегда может быть записан в виде (1).

Замечание. Если x и y – независимые переменные, то существуют две формы записи дифференциала: . Если x и y функции, то .

§6. Производная по направлению. Градиент

1. Производная по направлению

Рассмотрим функцию трех переменных u=f(x,y,z), определенную на множестве G. Пусть точка . Через точку М₀ проведём прямую l. Выберем произвольно на l точку М₁ и установим таким образом направление . Тогда l – прямая с выбранным направлением.

Пусть М(x,y,z) – переменная точка на прямой l. Через М₀М обозначим ориентированную длину отрезка М₀М, т.е. М₀М=|М₀М|, если направление отрезка совпадает с направлением l (точки М и М₁ лежат по одну сторону от точки М₀) и М₀М=-|М₀М|, если направление отрезка не совпадает с направлением l. Полное приращение функции:

.

Определение. Если существует конечный предел

,

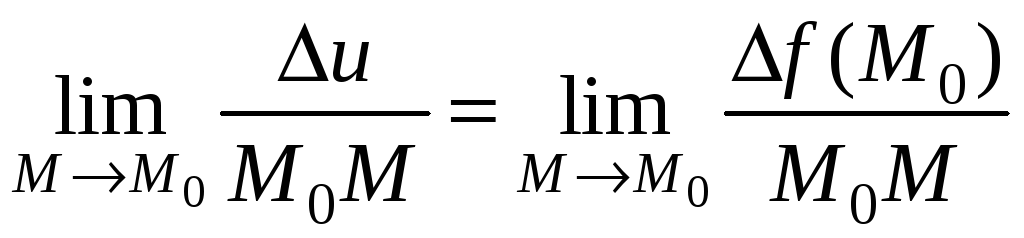то он называется производной функции f в точке М₀ по направлению l.

Обозначается .

Замечание. Производная функции f(x) в точке х₀- это скорость изменения функции в точке х₀. Частная производная - скорость изменения функции в точке М₀ по направлению оси Ох; частная производная - скорость изменения функции в точке М₀ по направлению оси Оу, а - по направлению оси Oz. Тогда - скорость изменения функции в точке М₀ по направлению l. Если направление l совпадает с положительным направлением оси Ох, то =. Аналогично для . Т.е. частные производные функции – это производные по направлению координатных осей.

Теорема (достаточное условие существования производной по направлению l). Если u=f(x,y,z) дифференцируема в точке М₀, то в этой точке существует производная по направлению, исходящему из точки М₀, и

, (1)

где - направляющие косинусы направления l (координаты единичного вектора в этом направлении).

Доказательство.

Проведём через точку М₀ прямую l возьмём на ней точку М, - ориентированная длина.

.

П о условию функция f дифференцируема в точке М₀. Следовательно, её полное приращение можно записать в виде

, (2)

где при . Разделим (2) на :

. (3)

Пусть ММ₀. Тогда . Тогда (проекции на оси координат) стремятся к 0. Следовательно, . Значит, правая часть равенства (3) при стремится к . Это означает, что существует и левой части: . Переходя в (3) к , получим (1).

Пример. . Найти производную в точке М₀(1,-2,3) в направлении вектора, соединяющего точки А(1;2;3) и В(3;3;1).

(2,1,-2), , .

, ,

, ,

, ,

.