2. Повторные пределы

Для функций нескольких переменных наряду с обычным понятием предела функции (при одновременном стремлении всех аргументов к их пределам) вводится понятие повторного предела, получаемого в результате ряда последовательных предельных переходов по каждому аргументу в отдельности в том или ином порядке. (Обычный предел функции n переменных называется n-кратным: двойным, тройным и т.д.)

Рассмотрим случай функции двух переменных. Пусть функция определена в области G. Пусть область G такова, что х может принимать (независимо от у) любые значения в некотором множестве Х, для которого х₀ – предельная точка, а переменная у (независимо от х) изменяется на множестве Y. Тогда G можно символически обозначить G =XY. При фиксированном значении переменной у функция f(x;y) становится функцией одной переменной х. Если при фиксированном yY существует , то, вообще говоря, этот предел зависит от наперед зафиксированного у: . Теперь можно рассматривать . Пусть он существует и равен А: =А. Тогда говорят, что в точке (х₀;у₀) существует повторный предел функции f(x;y)

. (1)

При этом 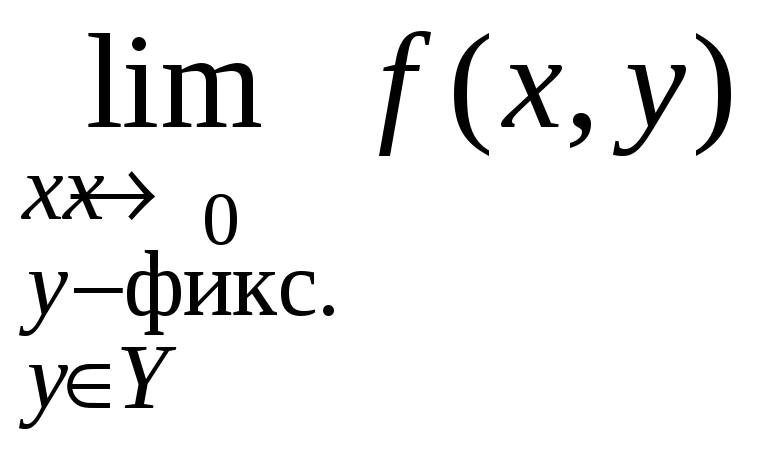называется внутренним пределом в повторном пределе (1).

Другой повторный предел

(2)

получится, если предельные переходы произвести в обратном порядке. В (2) внутренний предел - .

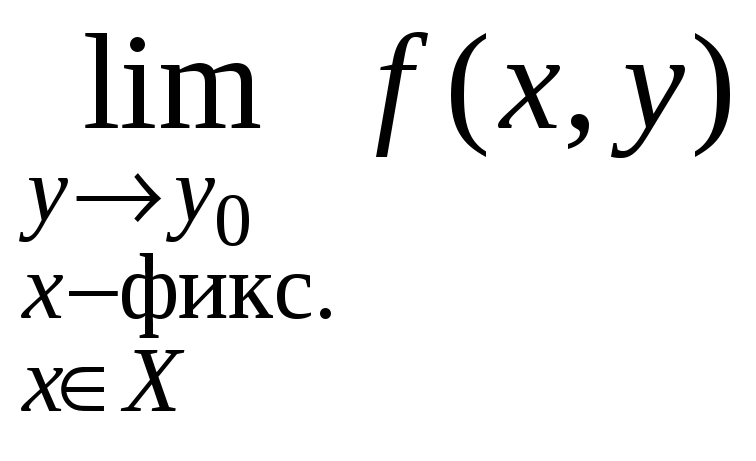Повторные пределы (1) и (2) вовсе не обязательно равны.

Пример 4. Вычислить повторные пределы функции 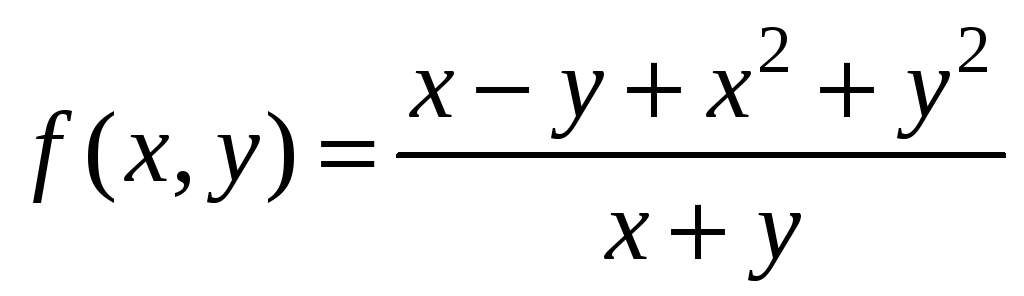в точке О(0;0).

 О(0;0)D(f ), является предельной точкой D(f ).

,

. 

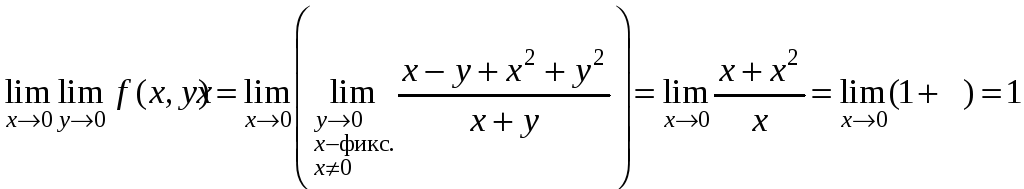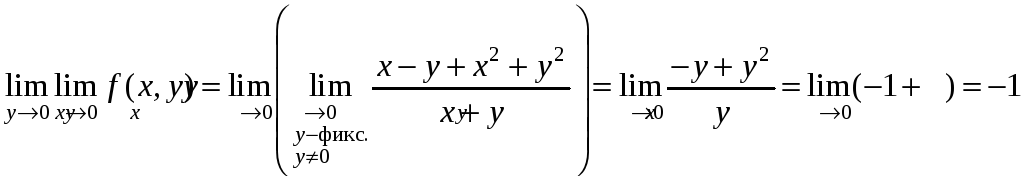Может случиться, что один из повторных пределов существует, а другой – нет.

Пример 5. Вычислить повторные пределы функции 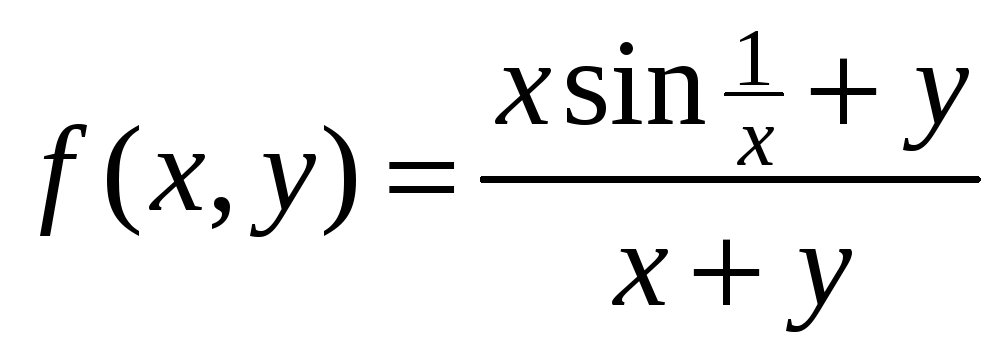в О(0;0).

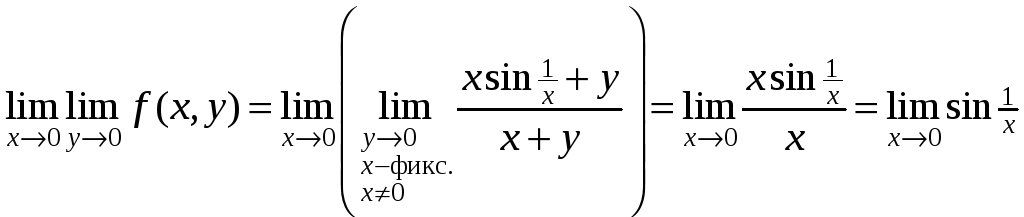 - не существует,

. 

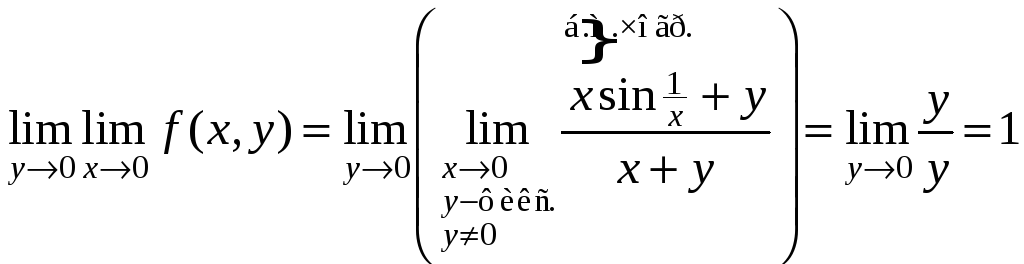Всякая перестановка двух предельных переходов по разным переменным должна быть обоснована. Одно из таких обоснований дает следующая теорема. Она также устанавливает связь между двойными и повторными пределами. Вообще говоря, из существования двойного предела не следует существование повторных пределов, и из существования повторных не следует существование двойного.

Теорема. Пусть в точке (х₀;у₀) существует (конечный или бесконечный) двойной предел , а также yY существует внутренний предел . Тогда существует повторный предел . Аналогично, если , и хХ существует внутренний предел , то существует повторный предел =А.

Если  и оба внутренних предела, то существуют и оба повторных предела, и .

Замечание. Обратное утверждение неверно. Если существуют и равны оба повторных предела, то двойной не обязательно существует.

Пример 6. .

 ,

,

,

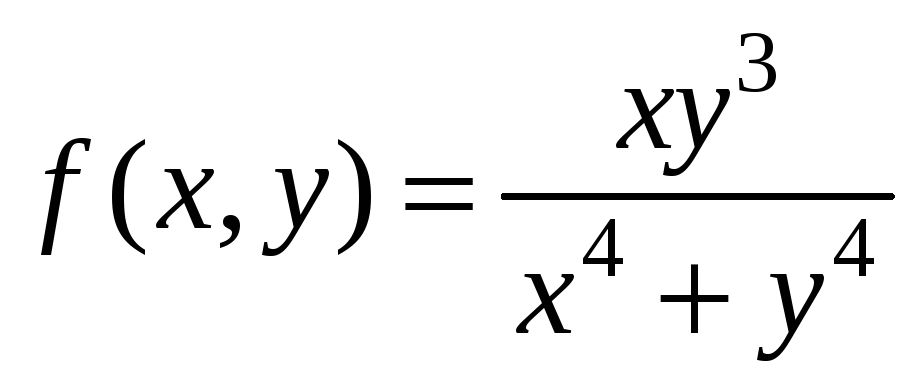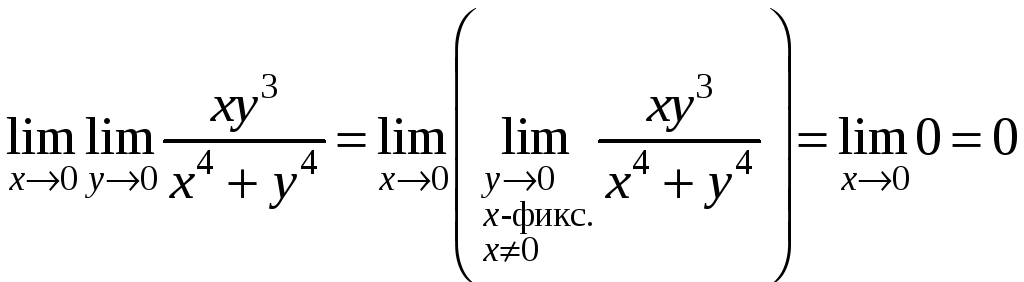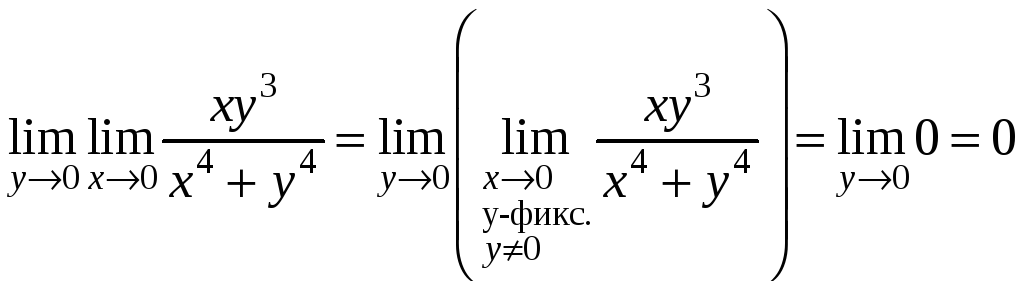но 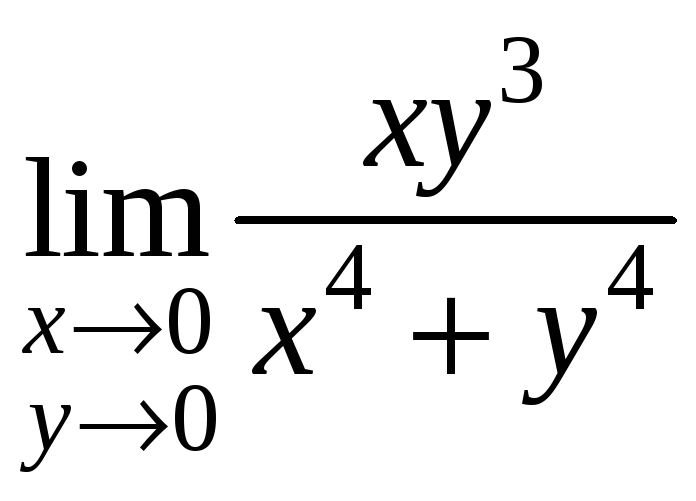не существует (см. пример 2). 

3. Непрерывность функции n переменных

Определение 1. Функция z=f(x,y) называется непрерывной в точке M₀(x₀;y₀), если она определена в некоторой окрестности этой точки, и предел функции равен значению функции в этой точке:

. (1)

Аналогично определяется непрерывность в точке функции n переменных.

Обозначим х=х₀+х, у=у₀+у. Тогда (1) можно переписать с. о.:

или .

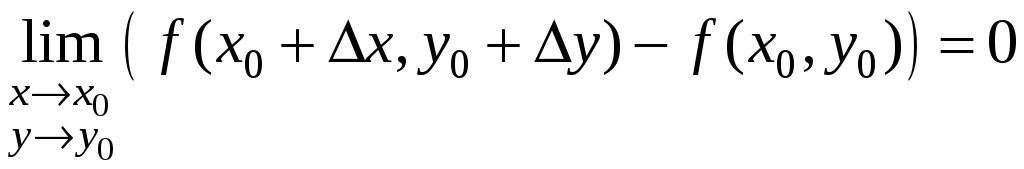Величина называется полным приращением функции z=f(x,y) в точке (x₀;y₀). Т. о., получаем эквивалентное определение непрерывности функции в точке.

Определение 2. Функция z=f(x,y) называется непрерывной в точке M₀(x₀;y₀), если бесконечно малым приращениям аргументов х и у соответствует бесконечно малое полное приращение функции: .

Если переменную у₀ оставить постоянной, а переменной х₀ придать некоторое приращение х, то функция z=f(x,y) получит приращение , которое называется частным приращением функции z в точке (х₀, у₀) по переменной х. Аналогично, если переменная х₀ остается постоянной, а у₀ получает приращение у, то - частное приращение функции z в точке (х₀,у₀) по переменной у.

Для функций нескольких переменных вводится понятие непрерывности по каждой из независимых переменных.

Определение. Частным приращением функции u=f(x₁,x₂,…x_n) в точке по переменной x_j называется величина

.

Определение. Функция u=f(x₁,x₂,…,x_n) называется непрерывной в точке М₀ по переменной x_j , если

.

Пример 7. Доказать, что функция

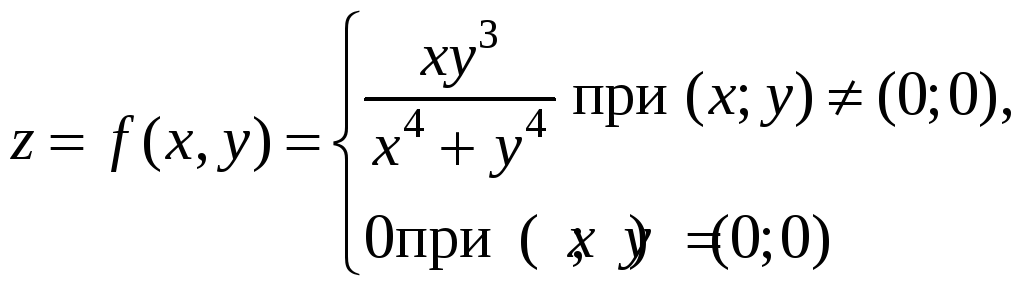
непрерывна в точке О(0;0) по каждой переменной х и у, но не является непрерывной по совокупности переменных.

 Частное приращение функции по переменной х в точке О(0;0):

.

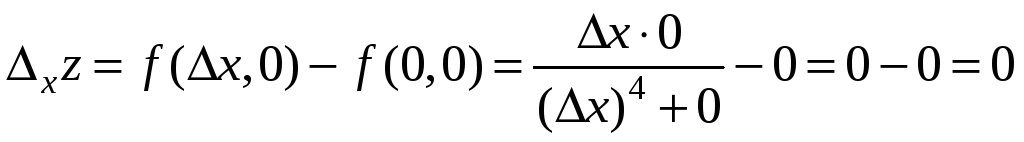
Следовательно, функция непрерывна в т. О(0;0) по переменной х.

Частное приращение функции по переменной у в точке О(0;0):

.

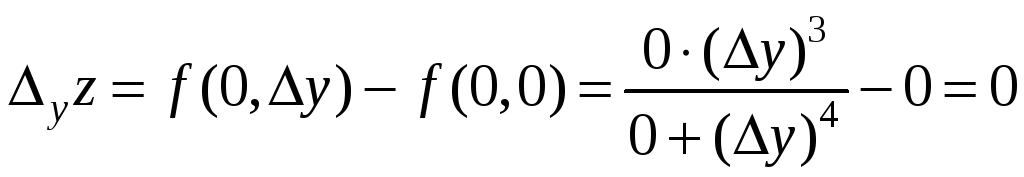
Следовательно, функция непрерывна в т. О(0;0) по переменной у.

Но функция не является непрерывной в т.О(0;0) по совокупности переменных, т.к. предел функции в этой точке не существует (см. пример 2 из п.2). 

Определение. Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.

Определение. Точка M₀(x₀;y₀), в которой не выполняется условие непрерывности, называется точкой разрыва функции z=f(x;y).

Это может быть, например, в следующих случаях:

1. z=f(x;y) определена во всех точках некоторой окрестности точки М₀, кроме самой точки М₀;

2. функция определена во всех точках V(М₀), но 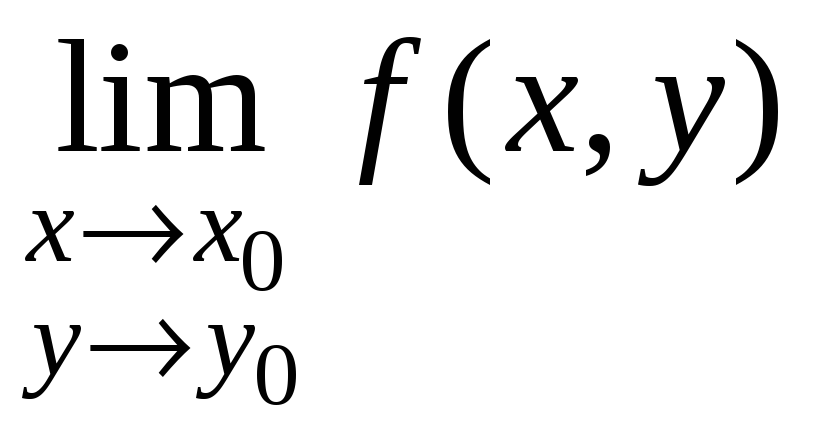не существует;

3. функция определена во всех точках V(М₀), и существует 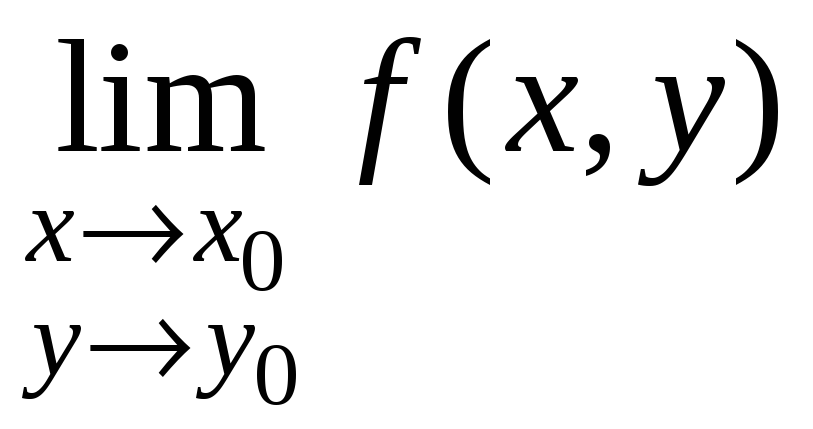, но .

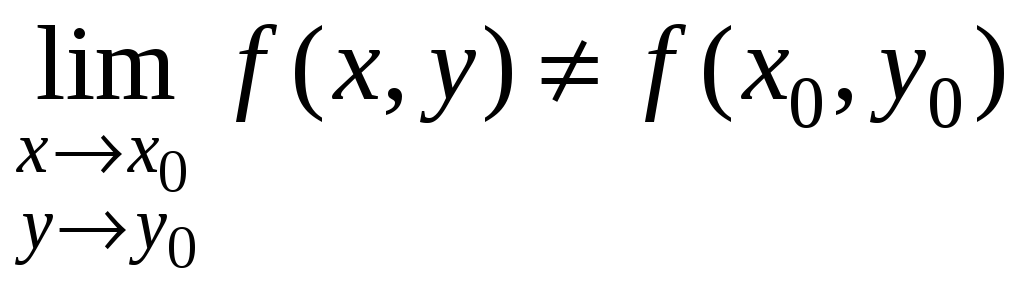Пример 2. Найти точки разрыва функции .

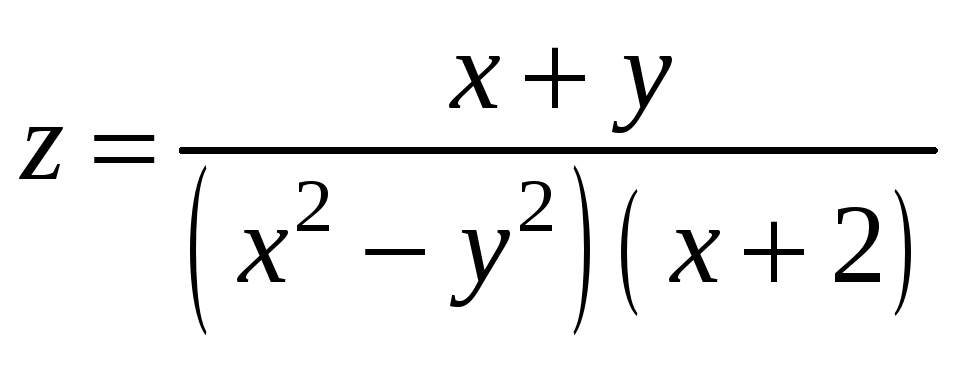 Функция может иметь разрыв лишь в точках, где =0 

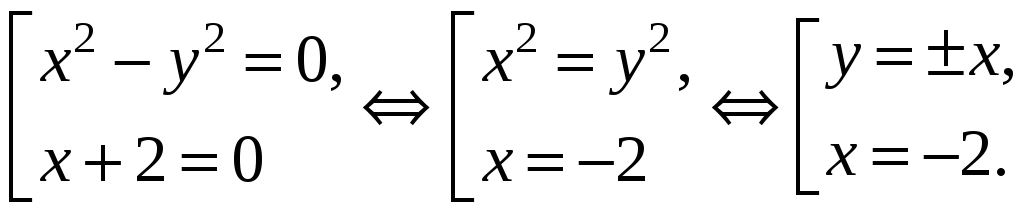
Итак, данная функция имеет разрыв на прямых у=х, у=-х, х=2. 