Дифференциальное исчисление функций нескольких переменных

§1. Метрические пространства. Пространство

Раньше изучались функции одной переменной f(x), которые были определены на . Рассмотрим некоторые свойства множеств, на которых задаются функции нескольких переменных.

Множество {x,y}, состоящее из двух элементов, называется парой. Пара, как и любое множество, определяется своими элементами. Упорядоченная пара (x,y) определяется еще и порядком следования элементов, т.е. . Аналогично определяется упорядоченная тройка, четверка и т.д. Упорядоченный набор из n элементов обозначается .

Декартовым (прямым) произведением множеств называется множество, содержащее все упорядоченные наборы , где , т.е.

.

Если , то называется числовой плоскостью. Каждой упорядоченной паре чисел (x,y) соответствует на плоскости, где введена декартова система координат, точка М(x,y), и наоборот, каждой точке на плоскости соответствует пара (x,y). Поэтому точка на плоскости отождествляется с упорядоченной парой.

Прямое произведение называется числовым трехмерным пространством.

- n-мерное пространство .

Упорядоченный набор называется точкой пространства , число - i-й координатой этой точки.

Обозначается , М.

В пространстве определяется сложение элементов, умножение элемента на действительное число. Пусть , :

1) ;

2) .

Пусть Е – непустое множество.

Определение. Метрикой (расстоянием) на множестве Е называется неотрицательная функция =(х,у)0, определенная х,уЕ и удовлетворяющая следующим условиям (аксиомам метрики):

1. (х,у)=0  х=у (аксиома тождества);

2. (х,у)=(у,х) (аксиома симметрии);

3. (х,y)(х,z)+(z,y) zЕ (аксиома треугольника).

Определение. Множество Е с введенной на нем метрикой  называется метрическим пространством и обозначается (Е,).

Т. о., метрическим пространством называется пара, состоящая из множества Е и метрики  на Е. Элементы метрического пространства Е называются его точками.

В пространстве метрика определяется следующим образом:

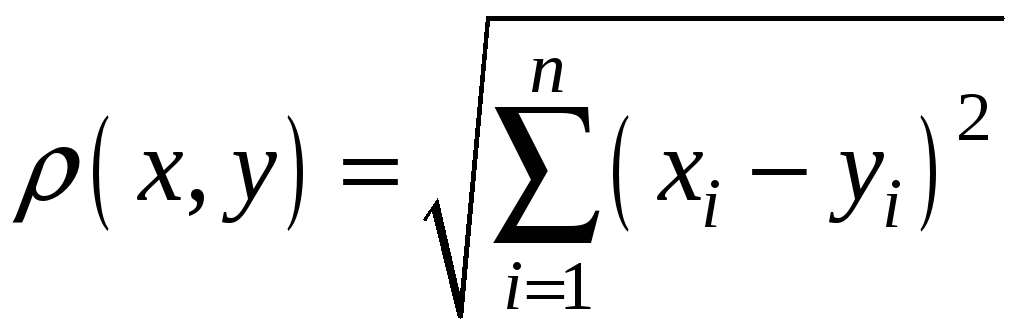, (1)

где и .

- метрическое пространство, n-мерное евклидово пространство (можно задать другую метрику и получить - другое метрическое пространство).

В случае n=1, т.е. в , ; в случае n=2, т.е. в , .

Покажем, что расстояние в , определяемое формулой (1), удовлетворяет всем аксиомам метрики.

1).

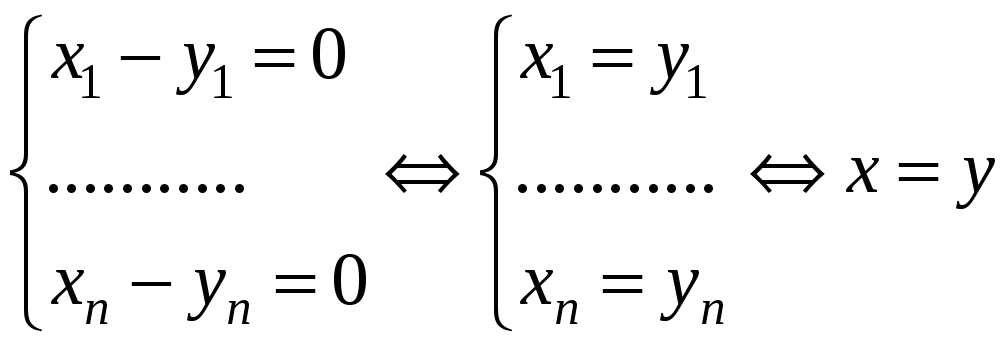2) (х,у)=(у,х), т.к. .

3) Пусть . Покажем, что

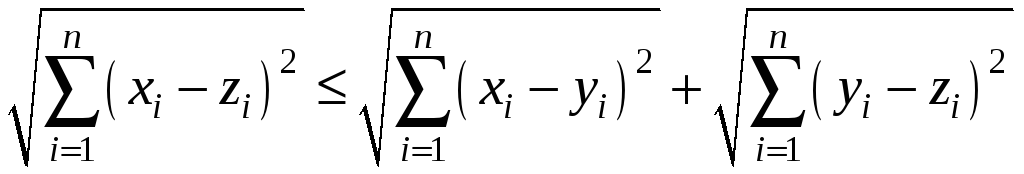. (2)

Докажем вначале, что имеют место неравенства:

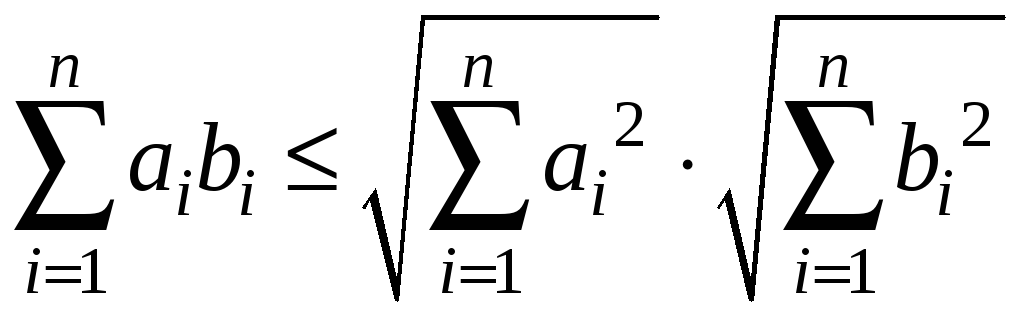- неравенство Коши-Буняковского (3)

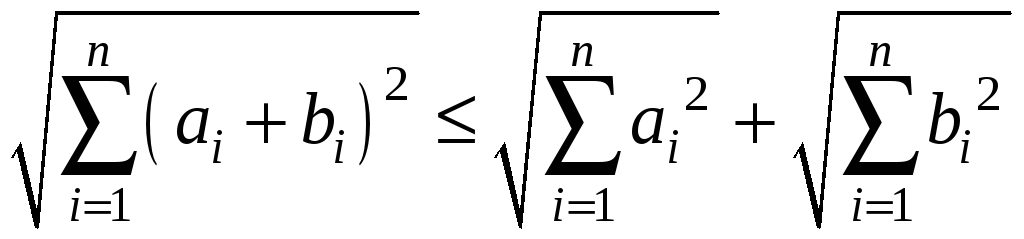- неравенство Минковского (4)

Доказательство (3).

Рассмотрим квадратный трехчлен относительно :

.

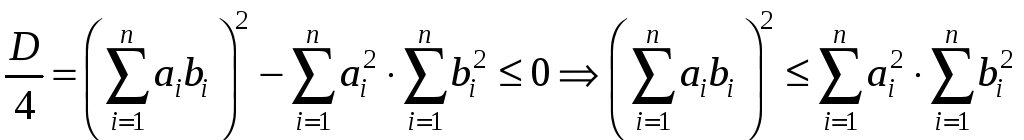Извлекая из обеих частей квадратный корень, получим (3).

Доказательство (4).

(4) следует из (3). Рассмотрим

.

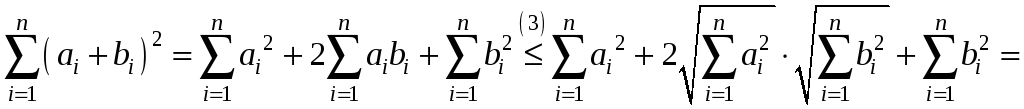
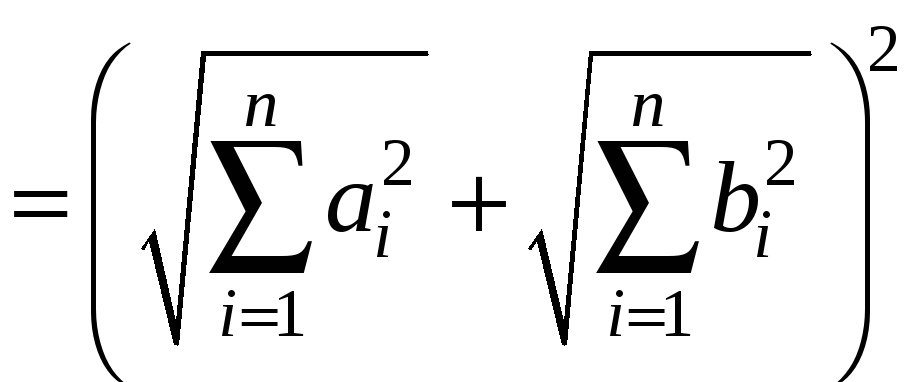Извлекая корень из обеих частей, получим (4).

Полагая в неравенстве Минковского a=x-z, b=z-y, получим (2), т.е. аксиома 3 для (х,у) выполнена.

Пусть - фиксированная точка, .

Определение 1. n-мерным открытым шаром в пространстве называется множество всех точек , удовлетворяющих неравенству : .

Фиксированная точка a называется центром шара, число - радиусом шара.

При n=1, .

При n=2, - открытый круг с центром в точке а(а₁,а₂), радиусом .

При n=3, - обычный шар (без ограничивающей его сферы ) в трехмерном пространстве.

Определение 2. Замкнутый шар в - .

Определение 3. Окрестностью точки называется любой открытый шар, содержащий эту точку.

Обозначается .

- проколотая окрестность точки а.

Пусть задано множество .

Определение 4. Точка a называется внутренней точкой множества Е, если существует окрестность точки а, целиком лежащая во множестве Е: .

Совокупность всех внутренних точек множества Е называется внутренностью множества Е. Обозначается int E.

Например, .

Определение 5. Точка называется внешней точкой множества Е, если , не содержащая ни одной точки множества Е.

Определение 6. Точка называется граничной точкой множества Е, если в любой окрестности точки а имеются как точки принадлежащие Е, так и точки не принадлежащие Е.

Граничная точка может как принадлежать, так и не принадлежать множеству.

Определение 7. Точка называется предельной точкой множества Е, если в любой окрестности точки а содержится хотя бы одна точка множества Е, отличная от а.

Определение 8. Точка называется изолированной точкой множества Е, если она не является предельной точкой множества Е.

У изолированной точки а множества Е , не содержащая ни одной точки множества Е.

Пример. .

Внутренние точки (1;3),

внешние точки ,

граничные точки {1;3;7},

предельные точки [1;3],

изолированная точка {7}.

Теорема 1. Точка а - предельная точка множества Е тогда и только тогда, когда в любой окрестности точки а содержится бесконечно много точек множества Е.

Определение 9. Множество Е называется открытым, если все его точки являются внутренними.

Определение 10. Множество Е называется замкнутым, если оно содержит все свои предельные точки.

Примеры. 1) (а;b), - открытые множества,

2) [a;b], - замкнутые множества,

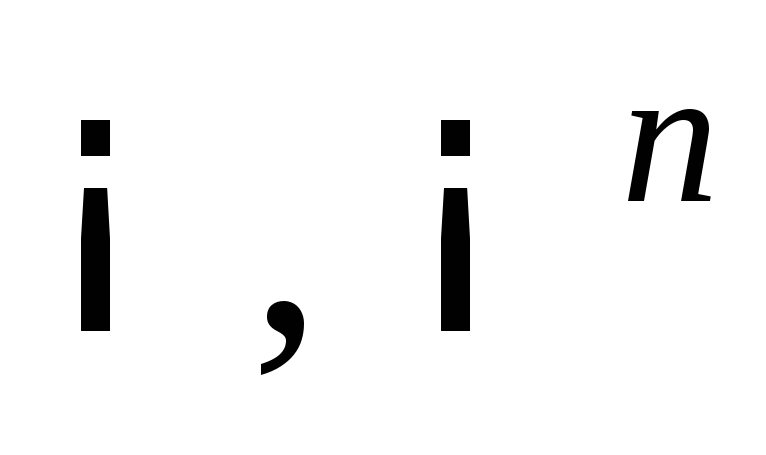3. - открытые множества.

Определение 11. Множество называется дополнением множества Е.

Теорема 2. Если множество Е открыто, то СЕ – замкнуто, если множество Е замкнуто, то СЕ – открыто.

Определение 12. Множество Е называется ограниченным, если существует замкнутый шар, содержащий в себе множество Е: .

Теорема 3. Множество Е ограничено.

Определение 13. Непрерывной кривой L в пространстве , соединяющей точки и называется множество , где функции непрерывны на [a;b], .

Определение 14. Множество Е называется связным (линейно связным), если любые две его точки можно соединить непрерывной кривой, целиком лежащей в этом множестве.

Определение 15. Множество называется областью, если оно открыто и связно.