6. Интегрирование по параметру

Теорема 9. Пусть G-простая область (то есть ), где функции (y) и (y) непрерывны на [c;d], а функции ₁(x) и ₁(x) непрерывны на [a;b]. Тогда если функция f(x;y) непрерывна на замыкании области G, то .

Теорема 9 является переформулировкой теоремы о сведении двойного интеграла к повторному, доказанной раннее. В частности, для прямоугольной области [a,b;c,d] получаем формулу: .

Говорят, что функцию (2) можно интегрировать по параметру у “под знаком интеграла”.

§2. Несобственные интегралы, зависящие от параметра

1. Равномерная сходимость интегралов

Пусть функция f(x;y) определена xa и yY.

Определение 1. Пусть при каждом y=y₀Y существует интеграл

.

Тогда интеграл (1)

называется сходящимся на множестве Y.

По определению несобственного интеграла с бесконечным пределом:

.

Интеграл (2)

представляет собой функцию от А и у.

Определение 2. Если стремление интеграла (2) к I(y) происходит равномерно относительно у в области Y, то интеграл I(y) называется равномерно сходящимся относительно у для указанных значений параметра.

Определение 2 означает, что >0 A₀a: A>A₀, yY выполнено

.

Определение 3. Сходящийся на множестве Y интеграл (1) I(y) называется равномерно сходящимся на этом множестве, если

.

Определение 2 равносильно определению 3 (доказательство аналогично проведенному в случае собственного интеграла).

Теорема 1 (необходимое и достаточное условие равномерной сходимости). Для того чтобы интеграл (1) сходился равномерно относительно у в области Y необходимо и достаточно, чтобы >0 A₀a: A>A>A₀, yY выполнялось .

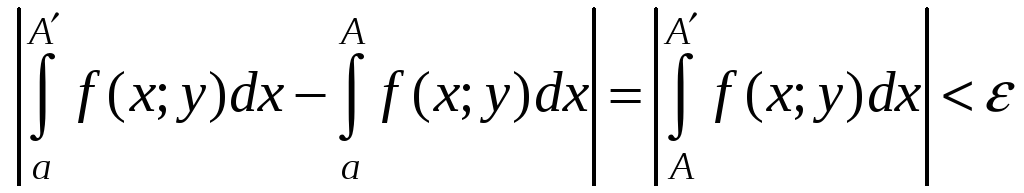Теорема 1 - переформулировка общего критерия равномерного стремления функции к пределу.

Признаки равномерной сходимости интегралов

Теорема 2 (признак Вейерштрасса). Если существует неотрицательная для (х), определенная на промежутке [a;+) такая, что:

1. |f(x;y)|(х) xa, yY;

2. сходится,

то интеграл (1) сходится равномерно относительно у на множестве Y.

Доказательство.

1) В силу признака сравнения интеграл (1) абсолютно, а следовательно, и просто сходится при любом yY (из (1) и (2)).

2) В силу сходимости >0 A₀a: A>A>A₀ выполнено .

3) .

По теореме 1 I(y) равномерно сходится на Y.

Теорема 3. Пусть функции f(x;y), g(x;y) определены при xa и yY, причем f(x;y) непрерывна по переменной х, а g(x;y) имеет непрерывную по х частную производную . Если:

1. функция g(x;y) при каждом yY монотонна по х и равномерно на множестве Y стремится к нулю при ,

2. интеграл ограничен как функция переменных A[a;+) и yY на множестве ;

то интеграл (3)

равномерно сходится на множестве Y.

При доказательстве используем следующее утверждение.

Вторая теорема о среднем для интегралов.

Если: 1) функции f(x) и g(x) ограничены и интегрируемы на [a;b];

2) функция g(x) монотонна при x[a;b],

то , где .

Доказательство теоремы 3.

1) Согласно второй теореме о среднем для интегралов при любых A,A: a<A<A, справедливо равенство:

, (4)

где .

(Предел не пишем, т.к. функция g(x;y) в силу дифференцируемости по х непрерывна по х).

2) По условию (п. 2) . Тогда

. (5).

Аналогично, . (6)

3) По условию . По определению

(8)

4) Из (4)-(7) следует имеет место оценка По теореме 1 (критерий равномерной сходимости) интеграл (3) равномерно сходится на множестве Y.

Теорема 4. Если: 1) интеграл сходится равномерно на Y;

2) функция g(x;y) ограничена и монотонна по х,

то интеграл (3) сходится равномерно на множестве Y.

(Без доказательства.)