
- •Интегралы, зависящие от параметра
- •§1. Собственные интегралы, зависящие от параметра
- •1. Определение интегралов, зависящих от параметра
- •2. Равномерная сходимость по параметру семейства функций
- •3. Предельный переход под знаком интеграла
- •4 Непрерывность по параметру
- •5. Дифференцирование по параметру
- •6. Интегрирование по параметру
- •§2. Несобственные интегралы, зависящие от параметра
- •1. Равномерная сходимость интегралов
- •2. Свойства несобственных интегралов, зависящих от параметра
- •§3. Интегралы Эйлера
- •Интеграл Эйлера первого рода (Бета-функция)
- •Интеграл Эйлера второго рода (Гамма-функция)
Интегралы, зависящие от параметра
§1. Собственные интегралы, зависящие от параметра
1. Определение интегралов, зависящих от параметра
П усть
усть
![]() ,
(y)
и (y)-
функции, определенные на Y,
(y)(y),
yY,
и функция f(x;y)
определена на множестве
,
(y)
и (y)-
функции, определенные на Y,
(y)(y),
yY,
и функция f(x;y)
определена на множестве
![]() .
Пусть при каждом конкретном значении
y=y0Y
функция f(x;y)=
f(x;y0)
будет интегрируема на отрезке
.
Пусть при каждом конкретном значении
y=y0Y
функция f(x;y)=
f(x;y0)
будет интегрируема на отрезке
![]() ,
то есть y0Y
,
то есть y0Y
 .
Тем самым определена функция
.
Тем самым определена функция
 ,
yY, (1)
,
yY, (1)
к оторая
называется интегралом,
зависящим
от параметра,
переменная у
называется параметром.
оторая
называется интегралом,
зависящим
от параметра,
переменная у
называется параметром.
Будем рассматривать случай, когда Y=[с;d], функции (y) и (y) непрерывны на [c;d] и (y)(y), y[c;d]. Соответствующую область обозначим G.
Частный случай интеграла типа (1): функции и постоянны, то есть интегралы вида:
 . (2)
. (2)
Задача: изучить свойства функции I(y) (непрерывность, правила дифференцирования и интегрирования) в зависимости от свойств функций f(x;y), (y) и (y).
П усть
усть
![]() ,
,
![]() и
и
![]() -
функции, определенные на Х,
-
функции, определенные на Х,
![]()
![]() ,
хХ,
и функция f(x;y)
определена на множестве
,
хХ,
и функция f(x;y)
определена на множестве
![]() .
Пусть при каждом конкретном значении
хХ
функция f(x;y)
будет интегрируема на отрезке
.
Пусть при каждом конкретном значении
хХ
функция f(x;y)
будет интегрируема на отрезке
![]() ,
то есть
,
то есть
 .
Ясно, что каждому хХ
будет отвечать свое определенное
значение этого интеграла. Значит, на Х
определена функция переменной (параметра)
х:
.
Ясно, что каждому хХ
будет отвечать свое определенное
значение этого интеграла. Значит, на Х
определена функция переменной (параметра)
х:
 . (1)
. (1)
Частный случай
интеграла типа (1):
функции
![]() и
и
![]() постоянны, то есть интегралы вида:
постоянны, то есть интегралы вида:
 ,
х[a;b].
,
х[a;b].
2. Равномерная сходимость по параметру семейства функций
Определение 1.
Пусть
![]() ,
y0-предельная
точка множества Y.
Пусть далее, функция (х)
определена для всех хХ,
а функция f(x;y),
для всех хХ
и yY
(на
,
y0-предельная
точка множества Y.
Пусть далее, функция (х)
определена для всех хХ,
а функция f(x;y),
для всех хХ
и yY
(на
![]() ).
Если:
).
Если:
-
для функции f(x;y) при yy0 существует конечная предельная функция
![]() ;
;
-
>0 >0, такое, что при | y-y0|< будет | f(x;y)-(x)|< сразу для всех хХ, то функция f(x;y) называется равномерно стремящейся на множестве X к функции (х) при yy0.
Обозначается
![]() ,
yy0.
,
yy0.
Заметим, что
-
в определении 1 не зависит от x;
-
из п.2 следует п.1.
Определение 2.
Функция f(x;y)
называется равномерно
стремящейся на множестве X
к функции (х)
при yy0,
если
![]() .
.
Теорема 1. Определения 1 и 2 равносильны.
Доказательство.
![]() 1. Необходимость:
определение 1
1. Необходимость:
определение 1![]() определение 2.
определение 2.
Имеем: >0
>0:
y:
| y-y0|<,
xX
выполнено |
f(x;y)-(x)|<.
Тогда по определению верхней грани
![]() .
.
Получили: >0
>0:
y:
| y-y0|<
выполнено
![]() .
.
Согласно определению
предела функции по Коши это означает,
что
![]() .
.
2. Достаточность:
определение 2![]() определение 1.
определение 1.
Имеем: >0
>0:
y:
| y-y0|<
выполнено
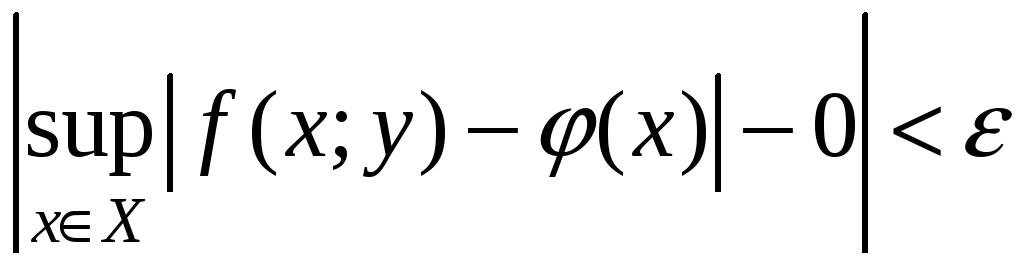 .
.
Т. к.
![]() ,
то и для всех хХ
тем более
,
то и для всех хХ
тем более
![]() ,
т.е. >0
>0:
y:
| y-y0|<,
xX
выполнено |
f(x;y)-(x)|<.
,
т.е. >0
>0:
y:
| y-y0|<,
xX
выполнено |
f(x;y)-(x)|<.
![]()
Теорема 2 (критерий
Коши). Для
того чтобы функция f(x;y)
при yy0
равномерно стремилась на множестве Х
к некоторой функции
![]() необходимо
и достаточно, чтобы
необходимо
и достаточно, чтобы
![]() было выполнено
было выполнено ![]() . (3)
. (3)
Доказательство.
![]() 1. Необходимость.
Обозначим предельную функцию (х).
По условию
1. Необходимость.
Обозначим предельную функцию (х).
По условию
![]() выполнено
выполнено
![]() ,
,
![]() выполнено
выполнено
![]() .
.
Обозначим
![]() .
Тогда
.
Тогда
![]() :
:
![]()
![]() .
.
2. Достаточность.
Имеем:
![]() выполнено
выполнено
![]() .
.
В том числе при
конкретном значении xX:
![]() выполнено
выполнено
![]() .
.
Тогда по критерию
Коши существования предела функции в
точке (предел функции в точке а
существует
![]() >0
=()>0:
>0
=()>0:
![]()
![]() ,
,
![]() выполнено
выполнено
![]() )
получим:
)
получим:
![]() .
.
Остается показать,
что стремление функции f(x;y)
к предельной функции (х)
при yy0
происходит равномерно. Переходя в (3) к
пределу при yy0,
получим
![]() выполнено
выполнено
![]() .
По определению 1 функция f(x;y)
при yy0
равномерно стремится на множестве Х
к функции (х).
.
По определению 1 функция f(x;y)
при yy0
равномерно стремится на множестве Х
к функции (х).
![]()
Замечание.
Если
![]() ,
,
![]() ,
то определение равномерной сходимости
по параметру превращается в определение
равномерной сходимости последовательности
функций
,
то определение равномерной сходимости
по параметру превращается в определение
равномерной сходимости последовательности
функций
![]() на множестве Х:
на множестве Х:
![]() выполнено
выполнено
![]() .
.
Пусть далее X=[a;b].
По известной теореме, если последовательность
![]() непрерывных функций равномерно сходится
к предельной функции на Х,
то и эта предельная функция будет
непрерывной на Х.
Перенесем это утверждение на общий
случай.
непрерывных функций равномерно сходится
к предельной функции на Х,
то и эта предельная функция будет
непрерывной на Х.
Перенесем это утверждение на общий
случай.
Теорема 3. Если функция f(x;y) при yY непрерывна по х в промежутке X=[a;b] и при yy0 равномерно стремится к предельной функции (х), то функция (х) будет непрерывна на Х.
Доказательство.
![]() Возьмем
Возьмем
![]() .
Покажем, что соответствующая
последовательность значений функции
.
Покажем, что соответствующая
последовательность значений функции
![]() .
.
По условию
![]() при yy0.
По определению 1
при yy0.
По определению 1
>0 >0: y: | y-y0|<, xX выполнено | f(x;y)-(x)|<.
Т.к. yny0,
то по определению:
![]() .
.
В том числе для
![]() .
.
Итак,
![]() выполнено
выполнено
![]() .
.
По определению
последовательность
![]() равномерно сходится к функции (х)
на множестве Х.
Тогда по теореме о непрерывности
предельной функции равномерно сходящейся
последовательности непрерывных функций
функция (х)
непрерывна на множестве Х.
равномерно сходится к функции (х)
на множестве Х.
Тогда по теореме о непрерывности
предельной функции равномерно сходящейся
последовательности непрерывных функций
функция (х)
непрерывна на множестве Х.
![]()
