1.5 Построение переходной функции

Переходная функция - это реакция системы на ступенчатое входное воздействие.

Для того, чтобы построить переходный процесс, используем обратное преобразование Лапласа от функции вида :

Следовательно переходная функция:

Рисунок 6 – График переходного процесса

Анализируя график, можно судить о том, что полученная линейная систе-

ма устойчива. По переходной функции определим характеристики:

установившееся состояние переходного процесса h_уст=0,202

максимальное значение переходного процесса h_max=0,023

Время первого согласования t₁=0,25c

Время нарастания t_н=40c

Время регулирования t_р=65 c

Перерегулирование σ=1,17%

4. Построение ачх сау

АЧХ строятся для того, чтобы определить косвенные оценки качества системы.

Для того, чтобы определить АЧХ системы, необходимо в передаточной функции р заменить на jw, знаменатель уравнения помножить на сопряженное выражение, выделить мнимую и вещественную части по формулам определить АЧХ, то есть:

(13)

Используя прикладную программу MATHcad построим АЧХ:

Рисунок 7 – Амплитудо – частотная характеристика САУ

Определим косвенные оценки качества системы:

Максимальная амплитуда А_max=5,51

Резонансная частота w_p=31,45 Гц

Частота среза, при которой амплитуда, равна 1 w_cp=29 Гц

Полоса пропускания: при w₁=31,407 Гц, w₂=31,476 Гц

1.7 Определение устойчивости по критерию Гурвица

Для устойчивости системы необходимо и достаточно, чтобы все миноры

определителя Гурвица были положительными.

По коэффициентам характеристического уравнения

(14)

составляется определитель Гурвица.

Для этого по главной диагонали определителя выписываются все коэффициенты характеристического уравнения, начиная со второго, затем вверх записываются коэффициенты с возрастающим индексом, а вниз с убывающим индексом.

Составленный определитель называется главным определителем Гурвица, он имеет порядок совпадающий с порядком характеристического уравнения. Из главного определителя составляются частные определители первого, второго, третьего и так далее порядков их образования из главного определителя.

Вычисляя главный определитель и частные определители, Гурвиц установил, для того, чтобы система была устойчива необходимо и достаточно, чтобы все определители были положительны. Если хотя бы один определитель отрицательный, то система неустойчива.

(15)

Вычислим миноры в определителе Гурвица:

(16)

(17)

Все миноры определителя Гурвица больше ноля, следовательно система устойчива.

8. Определение устойчивости по критерию Найквисту

Система является устойчивой, поскольку годограф Найквиста не охватывает точку с координатами (-1;0).

Рисунок 8 – Годограф Найквиста

Вывод.

Проведя ряд упрощений предложенной исходной схемы, была получена передаточная функция, преобразовав которую, был получен ряд значений характеризующих систему. Анализ значений показывает, что система работоспособна

и практически не имеет колебаний.

Система работает медленно, т.к. время регулирования системы t_р=65 c.

А также система имеет малую полосу пропускания, то есть полосу наилучшего прохождения сигнала: w₁=31,407 Гц, w₂=31,476 Гц.

2 Исследование НЕлинейной сАУ

2.1 Техническое задание

Рисунок 9 – Структурная схема нелинейной САУ

График, описывающий нелинейный элемент Н.Э. приведен на рисунке 10

y

4

-2

2

x

-4

Рисунок 10 – Релейная статическая характеристика с гистерезисом

2.2 Упрощение структурной схемы нелинейной САУ

Преобразуем данную схему чтобы выделить нелинейный элемент и путем преобразований, проделанных ранее, получим:

Рисунок 11 – Преобразование схемы САУ с нелинейным элементом

Заключим элемент W₃ в обратную связь с Н.Э. и разорвем ее:

W₁

1/W₃

W₃

Н.Э.

Где , (18)

(19)

Рисунок 12 – Дальнейшее преобразование схемы САУ с нелинейным элементом

Получим:

Н.Э.

W₁

Рисунок 13 – Итоговое преобразование данной схемы САУ с нелинейным элементом

2.3 Построение фазового портрета нелинейной САУ

Насильственно замыкаем данную цепь единичной ООС и запишем уравнение линейной части:

(20)

Передаточную функцию можно записать в виде или , подставляя в эту формулу значение передаточной функции получим:

(21)

Воспользуемся пакетом MathCad для решения этого дифференциального

уравнения.

Введем замену pⁱx=y_i и исключим из правой части уравнения производную, получим . Перенесем у₁ влево и распишем уравнение для х₁, принимающих разные значения на участках, характеризуемых графиком

статической характеристики нелинейного элемента.

Получим систему уравнений для участков (-∞;-2), (-2;2) и 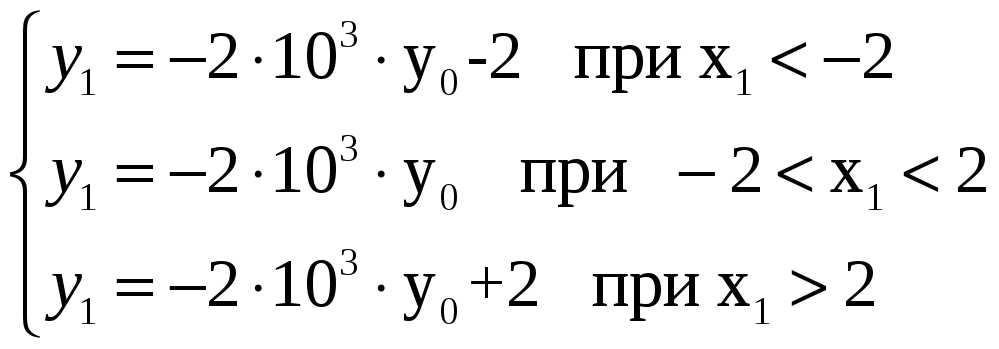(2;+∞):

(22)

Создадим матрицу для решения дифференциального уравнения:

(23)

В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицу начальных условий:

(24)

Возьмем количество точек равным 1000 и конечное время интегрирования 100, т.е.

Y=rkfixed(y, 0, 100, 1000, D) (25)

В итоге получим фазовый портрет (Рисунок 14).

Вывод.

На рисунке 14 представлен фазовый портрет нелинейной системы. До перехода через точку -2 работает первое уравнение системы, при переходе через эту

точку начинает работать второе уравнение. Третье уравнение работает при переходе через точку 2.

Рисунок 14 – Фазовый портрет рассматриваемой нелинейной системы

Характер фазовой линии такой, что она постоянно приближается к началу координат, т.е. нелинейная система с релейным элементом устойчива. При движении к состоянию устойчивости амплитуда колебаний постоянно уменьшается, а частота переключения растет. Получаем, что амплитуда колебаний в итоге примет нулевое значение, а частота колебаний станет бесконечно большой.

3 ИССЛЕДОВАНИЕ СИСТЕМЫ С ИМПУЛЬСНЫМ ЭЛЕМЕНТОМ

3.1 Преобразование структурной схемы САУ с импульсным элементом

По заданию проведем z-преобразование данной системы. Для этого первый элемент системы и сумматор заменим на цифровой элемент, передаточная функция которого равна 1. По итогам выполнения первой части курсового проекта можно записать:

Где (26)

(27)

(28)

(29)

(30)

Рисунок 11- Структурная схема САУ с импульсным элементом

Воспользовавшись предыдущими преобразованиями можно сразу написать общую передаточную функцию получившейся системы, так как несложно заметить она отличается от искомой на коэффициент К=1/0,8=1,25, и путем умножения его на передаточную функцию, найденную ранее, получим искомую:

(31)

Таким образом можно приступать непосредственно к z-преобразованиям.

3.2 Проведение z-преобразования передаточной функции САУ с импульсным элементом

Z-преобразование проведем по формуле:

(32)

Где и - показатели цифрового преобразования. В рамках курсовой работы принимает их равными 1;

- передаточная функция импульсной системы.

Воспользовавшись программным продуктом MathLAB можно получить искомую передаточную функцию уже в форме z-преобразования без использования предложенной методики:

(33)

3.3 Определение устойчивости САУ с импульсным элементом

Определим устойчивость полученной импульсной системы по Критерию Шур-Кона. Для устойчивости импульсной системы необходимо, чтобы коэффициенты характеристического уравнения были положительны:

В нашем случае характеристическое уравнение:

(34)

В характеристическом уравнении есть отрицательный коэффициент, следовательно, импульсная система не устойчива.

Проверим условия:

Составим определители Шур-Кона.

(35)

(36)

Посчитаем нечетные миноры матрицы. Для того, что бы система была устойчивой, чтобы нечетные миноры матрицы Шур Кона были меньше нуля, либо четные миноры матрицы были больше нуля.

Посчитав миноры в MathCAD, получили, что среди нечетных миноров присутствуют положительные, а именно .

Таким образом, получаем, что импульсная система неустойчива.

Построим переходный процесс, используя оператор INVLAPLACE, встроенный в программу MathCAD и получим переходный процесс:

(39)

Рисунок 12 – Переходный процесс импульсной системы

Вывод.

Проанализировав переходный процесс, полученный от данной импульсной системы, пользуясь вышепредставленными критериями и по графику переходного процесса, можно сделать вывод, что рассматриваемая система неустойчива.