2.2 Оценка запаса устойчивости сар по каналу управляющего воздействия

script 7

>> [Gm1,Pm1]=margin(W1)

Gm1 = Inf

Pm1 =46,8966

>> [Gm2,Pm2]=margin(W2)

Gm2 =10,2503

Pm2 = 39,2634

>> [Gm3,Pm3]=margin(W3)

Gm3 =Inf

Pm3 =35,8588

Таблица 2 Параметры запаса устойчивости САР по каналу управляющего воздействия

	∆L, дб запас по амплитуде	∆φ, град
П-рег	∞	46,8966
ПИ-рег	∞	39,2634
ПИД-рег	∞	35,8588

Вывод: Все САР имеют запас устойчивости так как у всех ∆L>6дб, ∆φ>30⁰

2.3 Оценка качества сар по каналу возмущающего воздействия

Рисунок 14.Структурная схема преобразованной САР

Переходную функцию САР по возмущению определяют по формуле замыкания:

(5)

где W(s)- Переходная функция разомкнутой САР

script 8

>> Fiz1=feedback(Wop,Wap1);

>> Fiz2=feedback(Wop,Wap2);

>> Fiz3=feedback(Wop,Wap3);

>> step(Fiz1,Fiz2,Fiz3)

Рисунок 15 Переходные характеристики по каналу возмущающего воздействия

Таблица 3 Параметры качества САР по каналу возмущающего воздействия

	ymax	ymax2	yуст	σ,%	Ε∞	tp	tн	tmax	æ	T	ω	n
П-рег	0,916	0,716	0,675	35.7	0,675	61.8	6.42	15.4	5,87	28.1	0.224	1.5
ПИ рег	0,862	0,407	0	Inf	0	214	0	14.4	2.11	29.1	0.216	1.5
ПИД рег	0.667	0.125	0	Inf	0	77.2	0	13.3	5.336	29.6	0.212	1.5

Вывод: П-регулятор имеет лучшее время быстродействия, но у него большая погрешность. ПИ-регулятор имеет самую большую величину перерегулирования σ и наибольшее время быстродействия, хотя нулевую погрешность. ПИД-регулятор как и ПИ-регулятор имеет нулевую погрешность, лучшее быстродействие по сравнению с ПИ-регулятором, но хуже чем П-регулятор и меньшую величину перерегулирования.

3. Оценка управляемости и наблюдаемости линейной сар

Для анализа управляемости и наблюдаемости САР необходимо математическую модель (ММ) системы привести к виду «вход-состояние-выход»

(6)

так как исследуемые свойства системы непосредственно связаны со структурой матриц А, В, С уравнений состояния.

Понятие наблюдаемости связано с возможностью определения переменных состояния по результатам измерения выходных переменных Y.

Понятие управляемости связано с возможностью приведения системы в заданное состояние с помощью управляющих (входных) воздействий U.

Для оценки управляемости САР вводят в рассмотрение матрицу управляемости:

Y=[B АВ A²B…A^n-1B] (7)

Первая теорема Калмана устанавливает условие управляемости: САУ полностью управляема тогда и только тогда, когда ранг матрицы управляемости Y равен размерности вектора переменных состояния n.

Для оценки наблюдаемости САР вводят в рассмотрение матрицу наблюдаемости:

H=[C^T A^TC^T A^T2C^T…A^{T n-1}C^T] (8)

Вторая теорема Калмана устанавливает условие наблюдаемости: САУ вполне наблюдаема тогда и только тогда, когда ранг матрицы управляемости H равен n.

3.1 Оценка управляемости и наблюдаемости линейной САР с П-регулятором

>> b2=0.825; b1=6.38; b0=3.74; a3=280; a2=131.8; a1=26.38; a0=5.04;

>> A=[0 1 0;0 0 1;-a0/a3 -a1/a3 -a2/a3]

A =

0 1.0000 0

0 0 1.0000

-0.0180 -0.0942 -0.4707

>> B=[0;0;1];

>> C=[b0/a3 b1/a3 b2/a3]

C =

0.0134 0.0228 0.0029

>> D=0;

>> sys=ss(A,B,C,D)

a =

x1 x2 x3

x1 0 1 0

x2 0 0 1

x3 -0.018 -0.09421 -0.4707

b =

u1

x1 0

x2 0

x3 1

c =

x1 x2 x3

y1 0.01336 0.02279 0.002946

d =

u1

y1 0

>> Y=[B A*B A^2*B]

Y =

0 0 1.0000

0 1.0000 -0.4707

1.0000 -0.4707 0.1274

>> r1=rank(Y)

r1 = 3

Следовательно, согласно критерию управляемости Калмана исследуемая САР полностью управляема, так как n=3.

>> d1=det(Y)

d1 = -1

Так как определитель не равен нулю, матрица управляемости является не вырожденной. Это также означает, что САР полностью управляема.

>> H1=[C;C*A;C*A^2]

H1 =

0.0134 0.0228 0.0029

-0.0001 0.0131 0.0214

-0.0004 -0.0021 0.0030

>> r11=rank(H1)

r11 = 3

Следовательно, согласно критерию наблюдаемости Калмана исследуемая САР полностью наблюдаема, так как n=3.

>> d11=det(H1)

d11 = 9.4771e-007

Так как определитель не равен нулю, матрица наблюдаемости является не вырожденной. Это также означает, что САР полностью наблюдаема

3.2 Оценка управляемости и наблюдаемости линейной САР с ПИ-регулятором

>> b3=0.84; b2=6.515; b1=3.953; b0=0.085; a4=280; a3=131.8; a2=26.51; a1=5.253; a0=0.085;

>> A=[0 1 0 0;0 0 1 0;0 0 0 1;-a0/a4 -a1/a4 -a2/a4 -a3/a4]

A =

0 1.0000 0 0

0 0 1.0000 0

0 0 0 1.0000

-0.0003 -0.0188 -0.0947 -0.4707

>> B=[0;0;0;1];

>> C=[b0/a4 b1/a4 b2/a4 b3/a4]

C =

0.0003 0.0141 0.0233 0.0030

>> C=[b0/a4 b1/a4 b2/a4 b3/a4]

C =

0.0003 0.0141 0.0233 0.0030

>> D=0;

>> Y2=[B A*B A^2*B A^3*B]

Y2 =

0 0 0 1.0000

0 0 1.0000 -0.4707

0 1.0000 -0.4707 0.1269

1.0000 -0.4707 0.1269 -0.0339

>> d21=det(Y2)

d21 =1

Так как определитель не равен нулю, матрица управляемости является не вырожденной. Это также означает, что САР полностью управляема.

>> r21=rank(Y2)

r21 = 4

Следовательно, согласно критерию управляемости Калмана исследуемая САР полностью управляема, так как n=4.

>> H2=[C;C*A;C*A^2;C*A^3]

H2 =

0.0003 0.0141 0.0233 0.0030

-0.0000 0.0002 0.0138 0.0219

-0.0000 -0.0004 -0.0018 0.0035

-0.0000 -0.0001 -0.0007 -0.0035

>> r22=rank(H2)

r22 = 4

Следовательно, согласно критерию наблюдаемости Калмана исследуемая САР полностью наблюдаема, так как n=4.

>> d22=det(H2)

d22 = -9.9331e-013

Так как определитель не равен нулю, матрица наблюдаемости является не вырожденной. Это также означает, что САР полностью наблюдаема

3.3 Оценка управляемости и наблюдаемости линейной САР с ПИД-регулятором

b4=1.269; b3=13.47; b2=31.27; b1=10.1; b0=0.407;

a4=351.3; a3=168.5; a2=53.27; a1=11.5; a0=0.407;

>> B0=b4/a4= 0.038

>> B1=(b3-B0*a3)/a4=0.0307

>> B2=(b1-B0*a2-B1*a3)/a4=0.0017

>> B3=(b1-B0*a1-B1*a2-B2*a3)/a4=0.0130

>> B4=(b0-B0*a0-B1*a1-B2*a2-B3*a3)/a4= -0.0063

>> Apid=[0 0 0 -a0/a4;1 0 0 -a1/a4;0 1 0 -a2/a4;0 0 1 -a3/a4]

Apid =

0 0 0 -0.0010

1.0000 0 0 -0.0220

0 1.0000 0 -0.1153

0 0 1.0000 -0.4988

>> Bpid=[B1;B2;B3;B4]

Bpid =

0.0307

0.0017

0.0130

-0.0063

>> Cpid=[0 0 0 1];

>> Dpid=0;

>> Ypid=[Bpid Apid*Bpid Apid^2*Bpid Apid^3*Bpid]

Ypid =

0.0307 0.0000 -0.0000 0.0000

0.0017 0.0308 -0.0003 0.0001

0.0130 0.0024 0.0290 0.0003

-0.0063 0.0161 -0.0056 0.0318

>> rpid=rank(Ypid)

rpid = 4

Следовательно, согласно критерию управляемости Калмана исследуемая САР полностью управляема, так как n=4.

>> dpid=det(Ypid)

dpid = 8.7167e-007

Так как определитель не равен нулю, матрица управляемости является не вырожденной. Это также означает, что САР полностью управляема.

>> Hpid=[Cpid;Cpid*Apid;Cpid*Apid^2;Cpid*Apid^3]

Hpid =

0 0 0 1.0000

0 0 1.0000 -0.4988

0 1.0000 -0.4988 0.1335

1.0000 -0.4988 0.1335 -0.0311

>> dpid1=det(Hpid)

dpid1 = 1

Так как определитель не равен нулю, матрица управляемости является не вырожденной. Это также означает, что САР полностью управляема.

>> rpid1=rank(Hpid)

rpid1 = 4

Следовательно, согласно критерию управляемости Калмана исследуемая САР полностью управляема, так как n=4.

4. Анализ нелинейной САР методом гармонической линеаризации

Предположим, что система автоматического регулирования, рассмотренная выше, имеет регулирующий орган с нелинейной характеристикой.

Метод гармонической линеаризации основан на предположении, что колебания на входе нелинейного звена являются синусоидальными, т.е.что

X(t)=Asinω_at,

Где А-амплитуда; ω_a-частота этих колебаний.

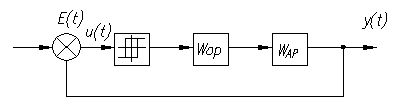
Рисунок 16. Структурная схема нелинейной САУ

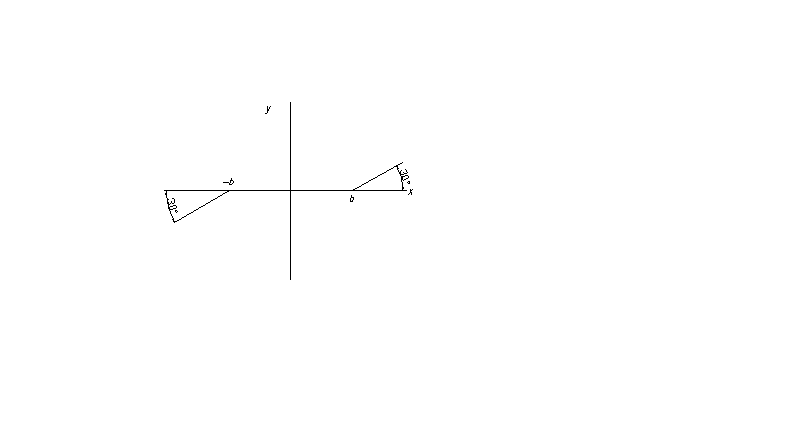
Рисунок 17. Статическая характеристика нелинейного усилителя

[1]

; ; b=3.8; k=tgα;

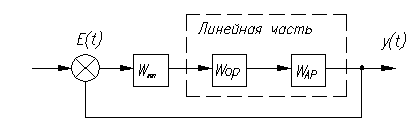
Рисунок 18. Структурная схема линеаризованной САУ

W_(S)=W_OP*W_AP (10)

(11)

где

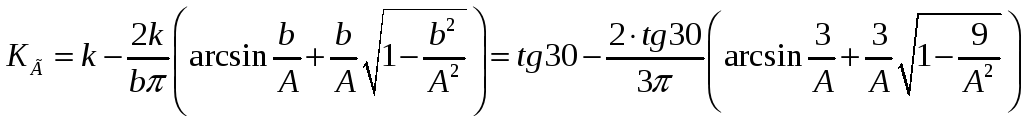
при А>b

Условие возникновения автоколебаний:

Wnon(A)W(jω)=-1 или ; W(jω)=Z(A);

Где

Уравнениние W(jω)=Z(A) решают графически, необходимо построить на одной комплексной плоскости годограф W(jω) и , если точка АЧХ Z(A), соответствующая увеличенной амплитуде А+∆А, охватывается АЧФХ линейной части W(jω), то рассматриваемые колебания устойчивы, в противном случае они не устойчивы.

В MATLAB

>> w=0.25:0.01:10;

>> W=(0.825.*(w*j).^2+6.38.*w*j+3.74)./(280.*(w*j).^3+131.*(w*j).^2+20.*w*j+1.3);

>> re=real(W);

>> im=imag(W);

>> plot(re,im)

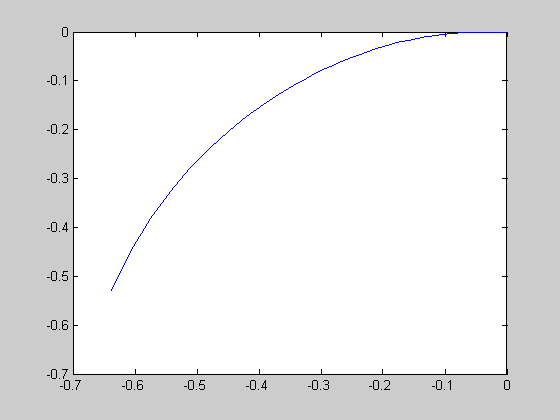
Рисунок 19. Годограф Найквиста

>> A=5:0.1:15;

>> Kg=(2*B/b*pi)./(asin(b./A)+(b./A).*sqrt(1-b^2./A.^2));

>> K=Kg+j.*Kg1;

>> Z=-1./K;

>> Re=real(Z);

>> Im=imag(Z);

>> plot(Re,Im)

Рисунок 20. Годограф Гольдфарба линейной части САУ

>> plot(re,im,Re,Im)

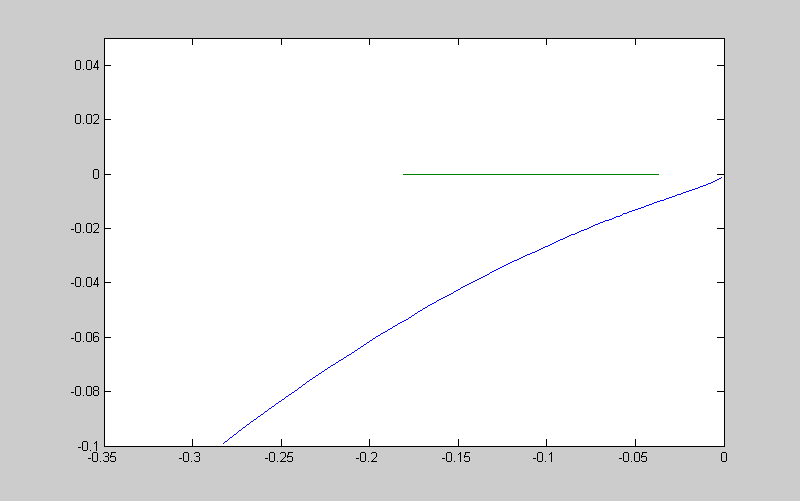
Рисунок 21. Годограф линеаризованной САУ

Вывод: Точка АЧХ Z(A), соответствующая увеличенной амплитуде А+∆А, не охватывается АЧФХ линейной части W(jω), поэтому рассматриваемые колебания не устойчивы.