Уравнение прямой, заданной точкой вектором нормали

Рассмотрим в прямоугольной декартовой системе координат Оху произвольную прямую d. Пусть на этой прямой задана точка , а также задан ненулевой вектор (рис. 2.19). Составим вектор .

у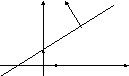

М

М₀ d

О х

Рис. 2.19

— (7) уравнение прямой, заданной нормальным вектором и точкой

Уравнение прямой с угловым коэффициентом

В прямоугольной системе координат уравнение прямой d: — (8) уравнение прямой с угловым коэффициентом, b — отрезок отсекаемый прямой от оси Оу (рис. 2.20), , где — угол между прямой и положительным направлением оси Ох.

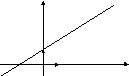
y d

b

О х

Рис. 2.20

Примеры решения задач

1. Составить уравнение прямой, проходящей через точку А(–2; 3) и перпендикулярной вектору .

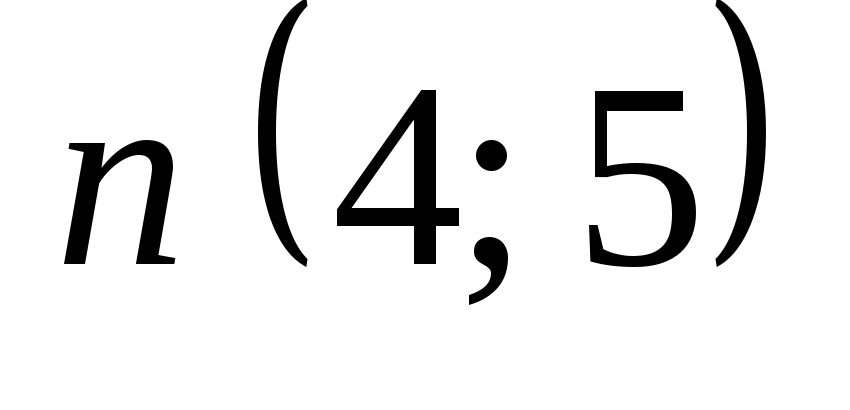Решение

Составим уравнение прямой, используя формулу (7) ,

— уравнение искомой прямой.

2. Даны координаты вершин А(1; –2), В(3; 2) и центра Е(1; 1) параллелограмма АВСD. Написать уравнения сторон параллелограмма.

Решение

Рис. 2.21

В параллелограмме ABCD (рис. 2.21) , поэтому Е — середина АС. Используя формулы координат середины отрезка, получим:

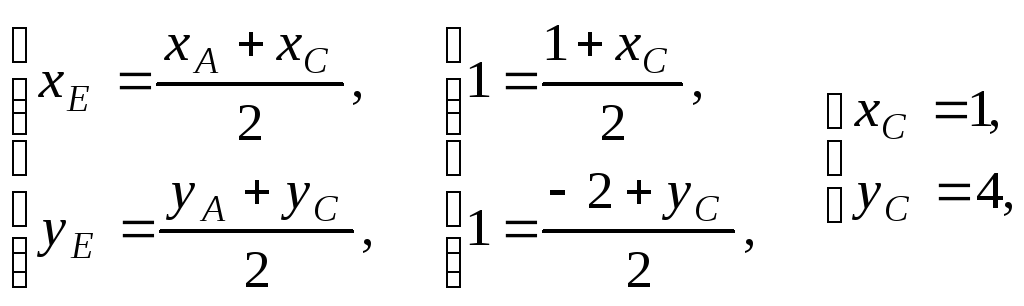С (1; 4).

Теперь у каждой стороны известны два определяющих элемента, что позволит составить их уравнения:

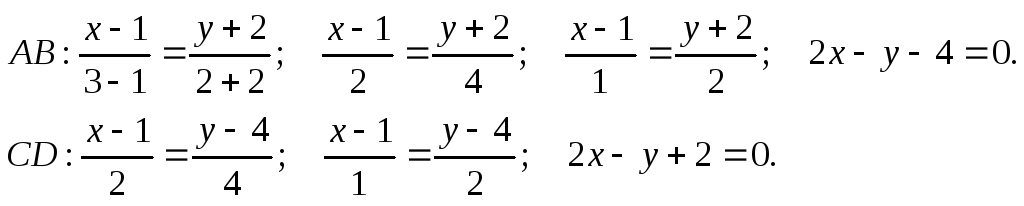
 СD.

.

.

(-2,2).

.

3. Прямая, проходящая через точку А (–2; 3), образует с осью Ох угол 135^о. Составить уравнение этой прямой.

Решение

Уравнение прямой будем искать в виде . Угловой коэффициент прямой . Искомая прямая проходит через точку А(–2; 3), поэтому координаты этой точки и удовлетворяют уравнению данной прямой, т. е. , откуда b=1. Следовательно, уравнение прямой имеет вид или .

§ 4. Расстояние от точки до прямой. Угол между прямыми

В прямоугольной системе координат расстояние от точки до прямой вычисляется по формуле

. (1)

Угол  между прямыми и определяется как острый угол между их направляющими векторами .

. (2)

Если прямая задана уравнением с угловым коэффициентом , то её направляющий вектор имеет координаты . Тогда приведенные формулы приобретают вид:

(3)

Перпендикулярность двух прямых определяется условием:

или .

Очевидно, что векторы и взаимно перпендикулярны. Этот факт можно использовать для составления уравнения перпендикуляра к данной прямой или направлению.