Примеры решения задач

1. Найти точку М пересечения медиан треугольника АВС (рис. 2.14), если А(1; 4), В(–5; 0), С(–2; –1).

Решение

Рис. 2.14

D — середина BС, .

Используя свойство медиан треугольника, получим . Если М(х,у), то

.

2. Найти площадь треугольника АВС, если А(2;1), В(3;4) и С(1;6).

Решение

. Используя определение косого произведения векторов, получим, что . .

, следовательно, .

§ 3. Различные способы задания прямой

Пусть d — некоторая прямая.

Определение. Каждый ненулевой вектор , параллельный прямой d или лежащий на данной прямой, называется направляющим вектором этой прямой.

Уравнение прямой, заданной точкой и направляющим векторому

M

M₀

M₁

O

у

d

х

Рис. 2.15

Прямая d вполне определяется точкой и направляющим вектором  d (рис. 15). Так как , где , то уравнение прямой можно записать в виде

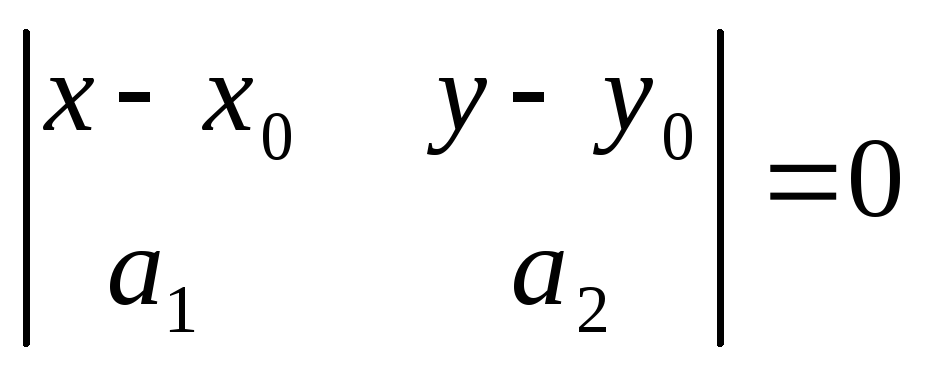, (1)

. (2)

— каноническое уравнение (3)

Уравнения (1)—(3) — различные виды уравнений прямой .

Уравнение прямой, заданной двумя точками

Как известно, через две данные точки проходит единственная прямая. Найдем уравнение этой прямой. Пусть прямая задана двумя точками (рис. 2.15). Обозначим координаты произвольной точки М (х, у)d. В качестве направляющего вектора можно взять вектор и воспользоваться уравнениями (1) и (3). Запишем соответствующие уравнения:

(4) ,

(5) — каноническое уравнение прямой проходящей через две заданные точки.

Общее уравнение прямой

Различные формы записи уравнения прямой (1—5), рассмотренные нами в предыдущих пунктах параграфа, имеют в принципе один и тот же вид:

(6) ,

где А, В, С — некоторые числа.

Уравнение (6) называется общим уравнением прямой, где является направляющим вектором этой прямой.

Определение. Любой ненулевой вектор, перпендикулярный к данной прямой, называется вектором нормали данной прямой и обозначается . Коэффициенты при переменных в общем уравнении прямой являются координатами вектора нормали

Рассмотрим некоторые частные случаи уравнения (6):

1. Если С = 0, то уравнение принимает вид и определяет прямую, проходящую через начало координат, так как ее координаты (0; 0) удовлетворяют этому уравнению (рис. 2.16)

Рис. 2.16

2. Если В = 0 (А  0), то уравнение принимает вид и определяет прямую, параллельную оси Оу (рис. 2.17). Это уравнение (при А  0) можно привести к виду или , где а — любое действительное число. В частности, если С = 0, то уравнение определяет ось ординат.

Рис. 2.17

3. Если А = 0 (В  0), то уравнение принимает вид и определяет прямую, параллельную оси Ох (рис. 2.18). Это уравнение (при В  0) можно привести к виду или , где в — любое действительное число. В частности, если С = 0, то уравнение определяет ось абсцисс.

Рис. 2.18