Примеры решения задач
-
Пусть АВСD — параллелограмм, О — точка пересечения диагоналей. Е, F — середины параллельных сторон ВС и АD. Построить на чертеже векторы:
а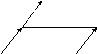
)
.
К
В С
А D
Рис. 2.6
,
где
(рис. 2.6).
б)
.
В Е С
А F D
Рис. 2.7
(рис. 2.7).
в
)
.
В С
О
А D
Рис. 2.8
(рис. 2.8).
г)
.
(рис. 2.9).
В С
О
А
D
Рис. 2.9
д)
.
В
Е С
О
А F D
Рис. 2.10
(рис. 2.10).
е
)
В Е С
О
А D
К
Рис. 2.11
=
где
(рис. 11).
-
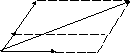
По данным векторам
и
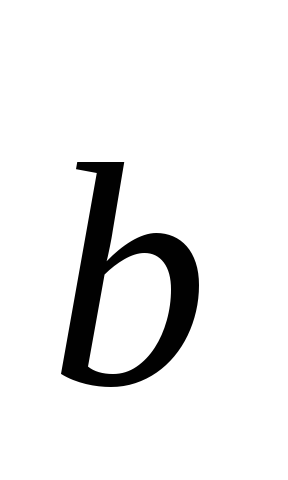построить вектор
.
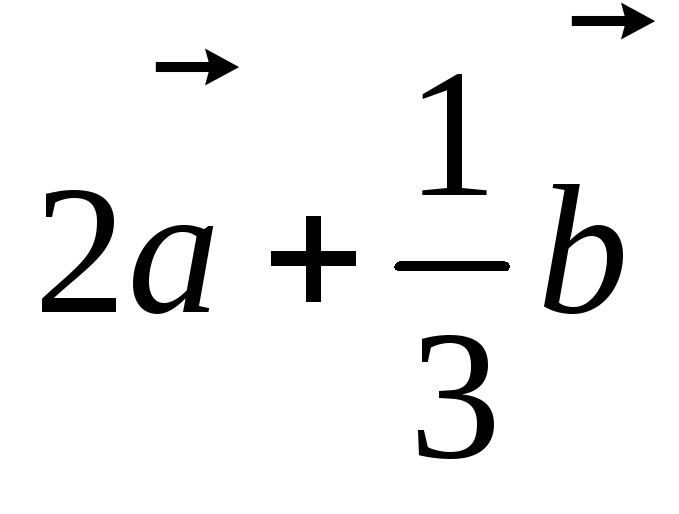Решение
Отложим
векторы
и
от одной точки (рис. 2.12):
.
Построим
.
По правилу параллелограмма
,
поэтому
.
В
С
В1
О А А1
Рис. 2.12
3.
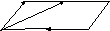
В ромбе ABCD
(рис. 2.13) выразить векторы
через векторы
и
.
Решение
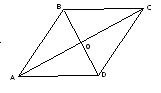
Рис. 2.13
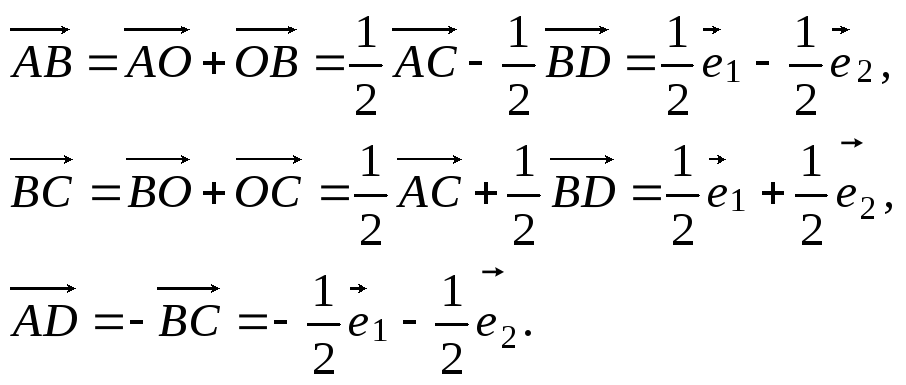
4.
Найти скалярное произведение векторов
и выяснить, являются ли они перпендикулярными.
Решение
,
следовательно, векторы
и
перпендикулярны.
5.
На плоскости
даны векторы
(–1;
5),
(3;
5),
(–2;
8),
(3;
1). Вычислить
.
Решение
=
((–1; 5) – (3;
5))∙((–2; 8) –(3; 1)) = (–4; 0)∙(–5; 7) =
=(–4)(–5)
= 20.
6.
Какой угол
образуют единичные векторы
и
,
если известно, что векторы
и
перпендикулярны?
Решение
=0
.
Учитывая, что
,
получим
.
Таким
образом, имеем
.
§ 2. Деление отрезка в данном отношении. Вычисление расстояния между точками. Косое произведение векторов. Площадь треугольника
Если
,
то
.
—
формула
для вычисления длины вектора
или
расстояния между точками М1
и М2.
Определение.
Точка М делит отрезок
в
отношении
,
причем
,
если
.
Если
и М (х, у)
точка делит отрезок М1М2
в отношении
,
то
.
Для
середины отрезка
.
Определение.
Косым произведением векторов
и
называется произведение длин этих
векторов на синус угла между ними, т. е.
.
Косое
произведение в координатах вычисляется
по формуле
=
.