Лекция 11
B-деревья
До сих пор мы рассматривали только бинарные деревья. Теперь рассмотрим деревья, имеющие большую степень ветвления. При этом хочется, чтобы сохранялись свойства, аналогичные свойству сбалансированности в сбалансированных деревьях. Этим условиям удовлетворяют B-деревья. Отметим, что B-деревья являются основным инструментом построения многих современных файловых систем (RaiserFS, JFS, XFS).
В B-деревьях в каждой вершине может содержаться несколько элементов (ключей). Высота дерева определяется как максимальное количество вершин в ветвях. Будем далее рассматривать случай, когда все элементы (ключи) в дереве различны.
В-дерево степени n определяется следующим образом
-
каждая вершина дерева, кроме корня, содержит от n-1 до 2n-1 элемента (ключей) и от n до 2n ссылок на дочерние элементы; корень дерева содержит не более 2n-1 элементов (ключей) и не более 2n ссылок на дочерние элементы
-
В-дерево идеально сбалансировано, более того, длины всех ветвей совпадают;
-
элементы в каждой вершине упорядочены по возрастанию
-
если в вершине содержится k элементов, то в ней содержится k+1 ссылок на дочерние вершины (кроме листьев, ссылок на дочерние вершины не содержащих);
-
элементы в вершине и ссылки на дочерние вершины сопоставляются следующим образом: про первую ссылку говорят, что она располагается до первого элемента, про последнюю – что она располагается после последнего элемента, остальные ссылки располагаются каждая – между некоторой парой элементов в вершине;
-
все элементы xi в поддереве V, ссылка на который расположена после некоторого элемента y больше y; все элементы xj в поддереве V, ссылка на который расположена до некоторого элемента z больше z. Пример В-дерева степени 3:
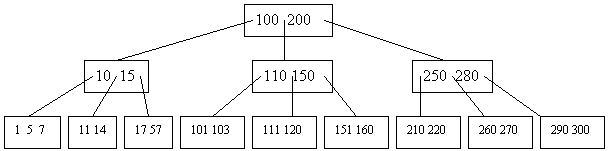
Как правило, В-деревья имеют достаточно большие степени. Например, их задают исходя из того, что одна вершина должна занимать один блок на диске.
На языке С тип данных для хранения одной вершины В-дерева степени 100 целых чисел можно определить следующим образом
#define NB 100
typedef struct BNode_
{
struct BNode_ *par;
int n;
struct BNode_ *child[2*NB];
int value[2*NB];
} BNode;
Здесь n – количество элементов, содержащихся в вершине, value[i] – значение i-го элемента, child[i] – указатель на соответствующего потомка. Заметим, что мы отвели на один целый элемент больше, чем нам требуется для хранения данных. Этим мы воспользуемся позднее – при поиске элемента в В-дереве.
Если элемент дерева занимает много места, то имеет смысл в вершинах хранить не сами данные, а указатели на них. Так, например, допустим, мы хотим создать дерево для хранения строк, в понимании языка С, тогда тип вершины можно определить следующим образом
#define NB 100
typedef struct BNode_
{
struct BNode_ *par;
int n;
struct BNode_ *child[2*NB];
char *str[2*NB-1];
} BNode;
Инициализировать такую структуру можно очень простой функцией:
void Init(BNode *node){memset(node,0,sizeof(BNode));}
После инициализации занесение строки в k-ый элемент вершины можно осуществить следующей функцией
void Insert(BNode *node, int i_elem, char *str)
{
if(node->str[i_elem]!=NULL)free(node->str[i_elem]);
node->str[i_elem]=strdup(str);
}