Удаление элемента из дерева
Удаление вершины из дерева поиска описано в параграфе Бинарные деревья поиска. Нам остается только сбалансировать, возможно, разбалансированное дерево.
Т.о. процедура удаления вершины v из сбалансированного дерева поиска сводится к следующему
-
нахождению вершины v, которую следует удалить,
-
ее удаления из дерева поиска (с помещением на ее место некторой вершины v'),
-
для каждой вершины ветви дерева от v' до корня следует проверять условие балансировки – если оно нарушилось, то операциями вращения следует произвести балансировку соответствующего поддерева.
Итак, в силу построения алгоритма удаления вершины из сбалансированного дерева, верна
Теорема. Из сбалансированного дерево поиска, состоящего из N вершин, можно удалить одну вершину за время O(log2 N).
Поиск минимального и максимального элемента в дереве
Не отличается от случая стандартных деревьев поиска.
Поиск следующего/предыдущего элемента в дереве
Не отличается от случая стандартных деревьев поиска.
Слияние двух деревьев
Для двух сбалансированных деревьев поиска T1 и T2 таких, что все элементы в T1 меньше или равны всех элементов в T2 : слияние деревьев в одно дерево поиска T.
Выбираем из дерева T2 наименьший элемент v (самый левый) и удаляем его из дерева T2 . Элемент v называется стыковочным. Для него верно: T1 v T2 .
Возможна ситуация, когда стыковочный элемент присутствует уже в постановке задачи.
Будем, для определенности, предполагать, что высота дерева T1 больше или равна высоте дерева T2.
Рассмотрим правую ветвь дерева T1 : {v1,…,vK}. В силу сбалансированности дерева имеем: h(vi) - h(vi+1) 2, тогда на этой ветви найдется вершина vl, такая что
h(vl) = h(T2) или h(vl) = h(T2)+1
Сольем дерево с корнем в vl и T2 с помощью стыковочной вершины v и подставим новое дерево на место старой вершины vl.
Вершина vl и все дерево, с нее начинающееся, окажутся сбалансированными. Высота же дерева, начинающегося с vl, увеличится на 1, т.к. h(T2) h(vl) .
Итак, в результате изменений дерева у одной вершины w длина соответствующего поддерева увеличилась на 1. Далее нам следует запустить стандартную процедуру балансировки дерева. Мы должны пройти ветвь, заканчивающуюся на w, от w до корня и в каждой вершине проверить баланс. Если он будет по модулю больше 1, то баланс в данной вершине следует скорректировать одним или двумя вращениями.
Если, при этом, длина данного поддерева восстановится до значения, которому она была равна до слияния деревьев, то далее процесс проверки сбалансированности производить не надо (т.к. дерево T1 до слияния было сбалансированным). Иначе, процесс проверки следует продолжить.
Отметим, что, в отличии от добавления к дереву одной вершины, в данном случае после уравновешения одной вершины процесс может не завершиться, т.к. возможен следующий вариант
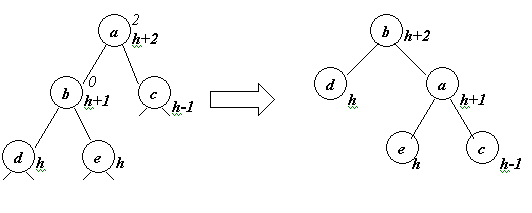
Этот вариант не мог реализоваться при добавлении одной вершины к дереву. В этом случае до слияния деревьев высота дерева с корнем a была равна h+1, а после слияния она стала равной h+2.
Итак, в силу построения алгоритма слияния двух сбалансированных деревьев, верна
Теорема. Для двух сбалансированных деревьев поиска T1 и T2 , состоящих из N1 и N2 вершин, имеющих высоты h1 и h2, таких, что все элементы в T1 меньше или равны всех элементов в T2 : слияние деревьев в одно сбалансированное дерево поиска T можно произвести за время T=O(log2 (N1+N2) ) или за время T=O(|h1-h2|).