Разбиение дерева по разбивающему элементу

Для данной вершины дерева v разбиение сбалансированного дерева поиска T на два сбалансированных дерева поиска T₁ и T₂ таких, что все элементы в T₁ меньше или равны v, и все элементы в T₂ больше или равны v.

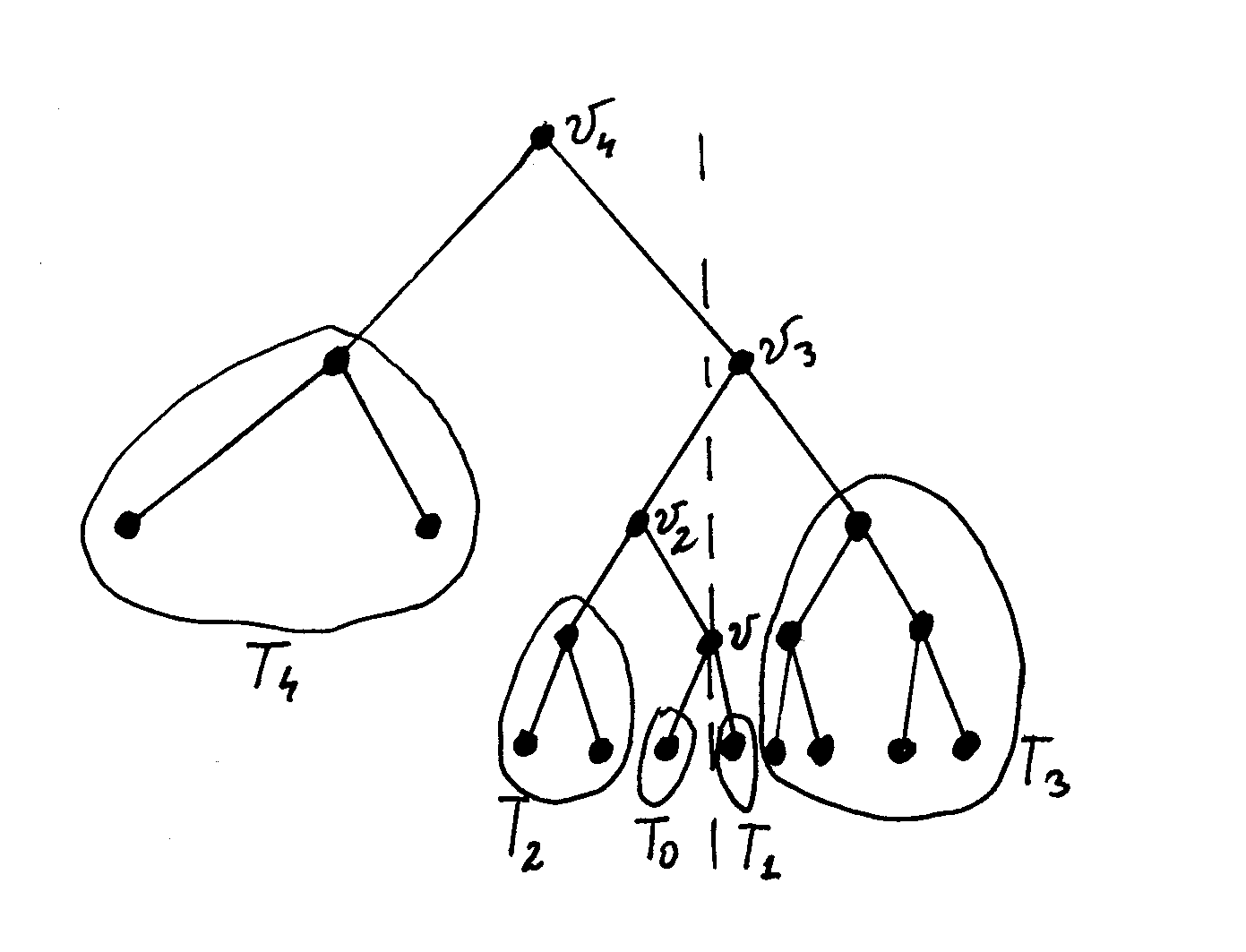
Алгоритм, практически полностью, совпадает с алгоритмом разбиения обычного дерева поиска. Только, теперь, нам следует пользоваться алгоритмом слияния деревьев для сбалансированных деревьев поиска.

Пусть высота дерева T₀ равна s₀. Пусть высоты деревьев, которые мы будем сливать, например, с деревом T₀ имеют значения s₁,…,s_K. Последовательность S={s₀,…,s_K } строго возрастающая, s_Kh, где h – высота дерева T. В силу алгоритма слияния деревьев с использованием стыковочного элемента, слияние двух деревьев X₁ и X₂ с высотой h₁ и h₂ дает дерево высотой MAX(h₁, h₂) или MAX(h₁, h₂)+1 .

Из чего, по индукции, сразу получаем, что после добавления очередного дерева T_i к дереву T₀, высота дерева T₀ будет равной либо s_i , либо s_i+1. Тогда, время работы всего алгоритма T=O(|s₀- s₁|+|s₁- s₂|+…+|s_K-1- s_K|)=O(log₂ N), где N – количество вершин в суммарном дереве.

Итак, верна следующая теорема

Теорема. Для данной вершины v сбалансированного дерева поиска T разбиение на два сбалансированных дерева поиска T₁ и T₂ таких, что все элементы в T₁ меньше или равны v, и все элементы в T₂ больше или равны v. может быть произведено указанным алгоритмом за время = O(log₂ N), где N – суммарное количество вершин в деревьях T₁ и T₂.

Лекция 10 Красно-черные деревья

Красно-черными деревьями называют бинарные деревья поиска, у которых для каждой вершины добавляется дополнительное свойство: вершина является черной или красной. При этом требуется выполнение следующих свойств:

• корень дерева – черный

• у каждой красной вершины потомки – черные

• в любых двух ветвях от корня до листа количество содержащихся черных вершин равно

Для простоты реализации в дерево добавляются фиктивные черные вершины: для каждой вершины дерева, при отсутствии у нее потомка, на место соответствующего потомка вставляется фиктивная черная вершина.

Вершины, отличные от фиктивных, называются внутренними. Будем далее называть листьями вершины, все потомки которых – фиктивные. При определении высоты дерева фиктивные вершины учитывать не будем.

Например, для задания одной вершины красно-черного дерева целых чисел в языке С можно использовать следующую структуру

typedef struct SBTree_

{

int IsRed;

int value;

struct STree_ *par;

struct STree_ *left, *right;

} SBTree;

здесь указатель par указывает на родительский элемент данной вершины, а left и right – на двух потомков, которых традиционно называют левым и правым. Целая переменная IsRed указывает – является ли данная вершина красной. Величина value называется ключом вершины.

Отступление на тему языка с. Поля структур.

В вышеприведенном примере кажется весьма накладным использовать целую переменную для хранения всего одного бита информации. Можно попробовать отвести под эту переменную меньше памяти:

typedef struct SBTreeX_

{

char IsRed;

int value;

struct STree_ *par;

struct STree_ *left, *right;

} SBTreeX;

Однако, в силу наличия выравнивания в структурах, для большинства современных машин размеры структур SBTreeX и SBTree окажутся равными.

Можно попробовать `отщипнуть’ один бит для переменной IsRed из целой переменной с ключом данной структуры value. Это можно сделать с помощью полей в структурах. Поля в структурах это – переменные целого типа, при описании которых после имени переменной пишется двоеточие и вслед за ним – количество бит, которые должны быть отведены под данную переменную. Например, в нашем случае, можно определить вершину дерева следующим образом:

typedef struct SBTree1_

{

unsigned int IsRed :1;

unsigned int value :31;

struct STree_ *par;

struct STree_ *left, *right;

} SBTree1;

При этом, следует понимать, что теперь каждая операция с членами структуры IsRed и value будет происходить довольно сложно (имеется реализация данной операции в кодах). Действительно, например, для изменения переменной value ее сначала требуется извлечь из структуры (используя битовые операции), изменить, а затем – поместить обратно.

Следует ожидать, что на IBM-совместимых ЭВМ работа со следующей структурой SBTree2 будет происходить медленнее, чем со структурой SBTree1:

typedef struct SBTree2_

{

unsigned int value :31;

unsigned int IsRed :1;

struct STree_ *par;

struct STree_ *left, *right;

} SBTree2;

Здесь используется следующий факт: на IBM-совместимых ЭВМ переменные типа int занимают 4 байта и байты располагаются в обратном порядке: от старшего к младшему. Поэтому для извлечения целой переменной из структуры SBTree1 требуется скопировать первые 4 байта структуры в отдельную переменную и обнулить старший бит этой переменной. Для структуры SBTree2 после извлечения первых четырех байт из структуры во внешнюю целую переменную надо еще дополнительно сдвинуть все биты целой переменной вправо на 1 бит.

Простейшие тесты подтверждают данное предположение. Естественно, что разные компиляторы по разному оптимизируют работу с битовыми полями. Так, например, компилятор Microsoft Visual C++ почти нивелирует разницу в скорости работы со всеми описанными типами структур (разница в скорости элементарных операций с данными структурами оценивается примерно 10-20%). Для используемого же компилятора gnu C++ разница в скорости оказалась – вдвое.

Отметим, что данный подход применим далеко не всегда. Поля в структурах обязаны иметь тип unsigned int. В современных версиях языка С это требование немного ослабло и вместо этого типа часто можно использовать другие целые типы, но, например, тип float все равно использовать нельзя. Пример использованной программы прилагается.