4.3. Анализ замкнутой системы

Вычислим матрицы системы разностных уравнений в форме пространства состояний:

[Ard1,Brd1,Crd1,Drd1]=feedback(Ad,Bd,Cd,Dd,Ard1,Brd1,Crd1,Drd1);

abs(eig(Ard1))

ans= 1.0e+004 *

2.5690

2.5686

0.0003

0.0001

0.0000

0.0000

0.0001

0.0001

Система явно неустойчива – покажем это на графиках:

[numrd2,denrd2]=ss2tf(Ard1,Brd1,Crd1,Drd1);

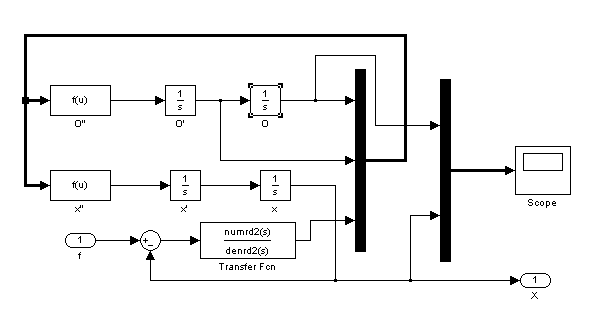
Рис. 4.4. Гибридная модель системы

При симуляции получаем ошибку (рис. 4.5).

Рис. 4.5. Ошибка системыMATLAB/Simulink

Таким образом, полученная нами система не только неустойчива, но и не реализуема на практике, т.к. даже не может быть промоделирована с использованием текущих технических средств.

Заключение

В результате курсового проектирования на базе нелинейной модели объекта в форме системы дифференциальных уравнений четвертого порядка получена линеаризованная модель объекта, которая позволила провести анализ устойчивости положения равновесия, анализ управляемости и наблюдаемости. Сделан вывод о необходимости синтеза регулятора, стабилизирующего неустойчивое положение маятника на каретке. По линейной непрерывной модели объекта, полученной для малых отклонений от положения равновесия, с помощью метода размещения собственных значений синтезирован регулятор состояния. Для реализации динамического регулятора был также синтезирован наблюдатель состояний. В результате была получена система, состоящая из нелинейного объекта и регулятора, не позволяющего стабилизировать систему даже при небольших ее отклонениях от положения равновесия.

Для реализации дискретного регулятора было использовано два способа: дискретизация непрерывного регулятора и синтез дискретного регулятора на основе дискретной линеаризованной модели объекта. На основе анализа результатов была подтверждена эквивалентность этих способов. Т.к. ни одним из них стабилизировать объект не получилось.

При синтезе дискретного регулятора, мы пытались уменьшить период дискретизации, чтобы повысить устойчивость объекта. Снизив период дискретизации до

T=0.000002;

[Ad, Bd, Cd, Dd] = c2dm(A,B,C,D,T);

abs(eig(Ad))

ans= 1.0000

1.0000

1.0000

1.0000, мы добились того, что объект стал находится на границе устойчивости. Но реализация такого регулятора сложна и бессмысленна, т.к. объект неуправляем и не наблюдаем.

Задачи, поставленные в курсовом проекте не решены, что позволяет говорить о том, что цель проекта не достигнута.

Список используемой литературы

1. С. Е. Душин, н. С. Зотов, д. Х. Имаев, н. Н. Кузьмин, в. Б. Яковлев “Теория автоматического управления”.- м.:”Высшая школа”, 2003

2. “Matlab Help” 1994-2006 The MathWorks, Inc.

25