курсовая работа / KURSOVAY_TAU / ЛИНЕЙНАЯ_ЧАСТЬ

1. Линейная часть.

1. Упростим систему.

Тогда структурная схема будет выглядеть следующим образом:

Объединим W6 c W12 :

Структурная схема примет вид:

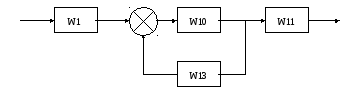
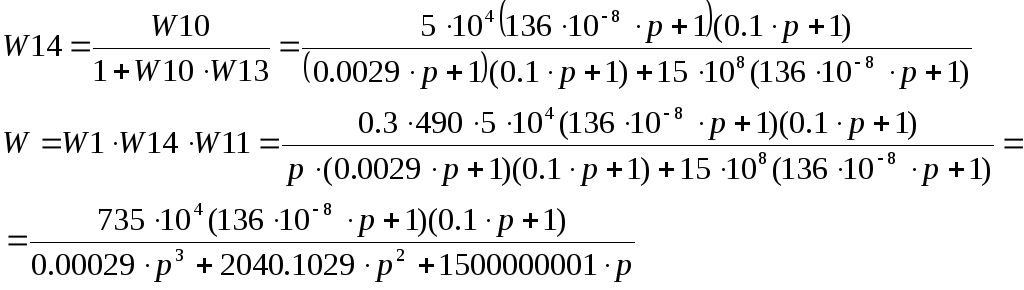
2. Определим устойчивость системы.

Определим устойчивость системы с помощью критерия Гурвица. Характеристическое уравнение найденной передаточной функции имеет вид:

0.00029p³+2040.1029p²+1500000001p=0

Используя данное уравнение составим главный определитель Гурвица.

Из главного определителя выделим диагональные миноры:

Система является устойчивой если главный определитель Гурвица и все его диагональные миноры больше нуля. В данном случае система находится на границе устойчивости, так как главный определитель Гурвица равен нулю.

Для достоверности полученных данных воспользуемся еще одним критерием -

критерием устойчивости Ляпунова. Для этого найдем корни характеристического полинома полученной передаточной функции.

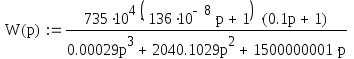
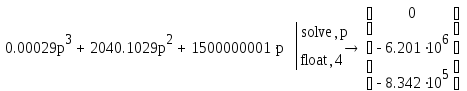
Так как в результате получили два отрицательных корня и один нулевой, то, согласно критерию Ляпунова, можно сделать вывод, что система находится на границе устойчивости.

Передаточную функцию можно записать следующим образом:

или

3. Построим переходный процесс системы.

Переходная функция- это реакция системы на единичное ступенчатое воздействие.

, где W1(s)- передаточная функция замкнутой системы, которая определяется по формуле:

Тогда

Построим график переходного процесса.

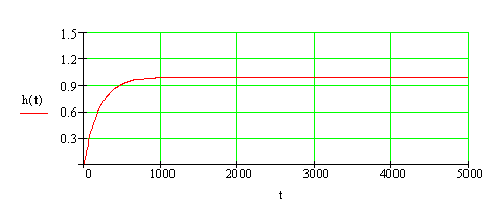
По виду графика переходного процесса также можно сделать вывод, что система устойчивая.

По графику переходного процесса определим прямые оценки качества системы:

1. время переходного процесса t_п =940 c

2. время первого согласования t₁=925 c

3. установившееся значение h_уст =1

4. максимальное значение h_мах =1

5. перерегулирование %

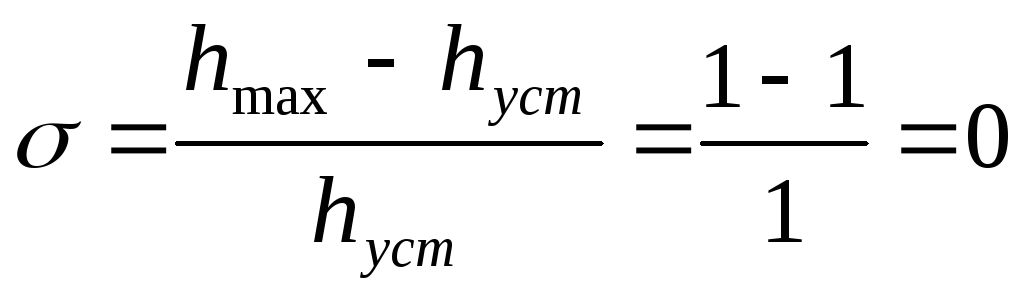1.4 Построим АЧХ и ФЧХ системы.

П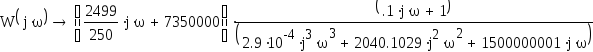ерейдем к частотной форме записи передаточной функции разомкнутой системы. Для этого заменим , получим:

где - мнимая единица;

Определим действительную и мнимую часть.

Найдем АЧХ системы по формуле:

Построим график АЧХ.

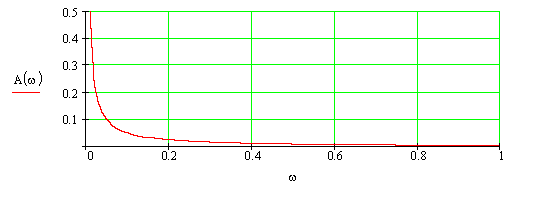
По графику АЧХ частота среза: ω_ср=0,005 рад/с

Найдем ФЧХ системы по формуле:

или

Построим график ФЧХ.

1.5 Построим ЛАЧХ и ЛФЧХ.

Определим собственные частоты каждого звена данной передаточной функции:

lg(ω1)=1 lg (ω2)=6.8 lg (ω3)=5.92 lg (ω4)=5.86

тогда

График ЛАЧХ будет иметь вид:

Построим график ЛФЧХ по функции:

или

EMBED Mathcad

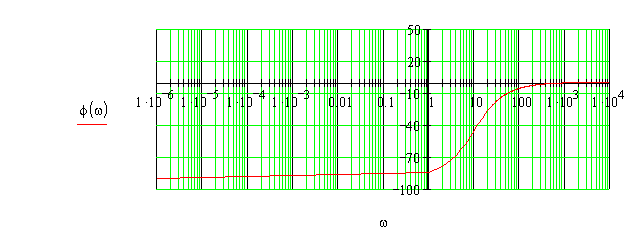
Запас устойчивости по фазе: ψ = 90°