курсовая работа / KURSOVAY_TAU / Нелинейная_часть2

2. Нелинейная часть.

Структурная схема с нелинейным элементом имеет вид:

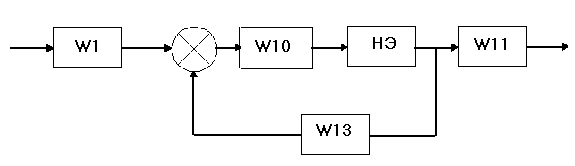
Здесь,

Нелинейный элемент имеет статическую характеристику вида:

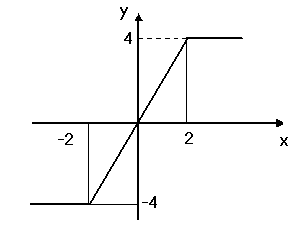
С точки зрения энергетических затрат, использование нелинейных элементов нецелесообразно. Проанализируем статическую характеристику данного нелинейного элемента на трех ее участках.

- передаточная функция звена.

Тогда на первом и третьем участках , то есть на них система не работоспособна.

Работает система только на втором участке, где или по-другому можно записать:

Таким образом, нелинейный элемент в данной схеме целесообразней заменить линейным элементом с передаточной функцией W15=K, где К=2 – коэффициент усиления.

Для исследования данной системы ее структурную схему преобразовывают так, чтобы получить простую одноконтурную схему, в которой нелинейный элемент и линейная часть будут соединены последовательно.

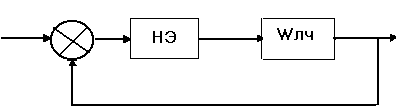
Преобразуем исходную схему к стандартному виду. Для этого разомкнем схему перед нелинейным элементом, то есть преобразуем ее так, чтобы здесь был вход в систему. Тогда выходная величина будет у1. Регулирующее воздействие должно быть приложено к новому входу системы. Согласно правилам преобразования структурных схем регулирующее воздействие перд тем как попасть на вход нелинейного элемента должно пройти через звенья W1 и W10. В изображении по Лапласу это выглядит следующим образом:

Все остальные связи между звеньями сохраняются, а структурная схема принимает следующий вид:

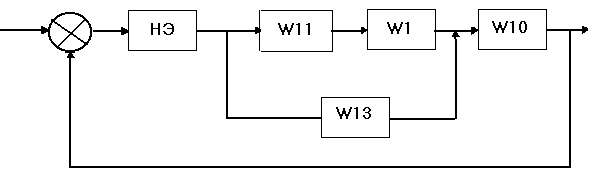
эквивалентная линеаризованная структурная схема примет вид:

2.1 Определим передаточную функцию системы.

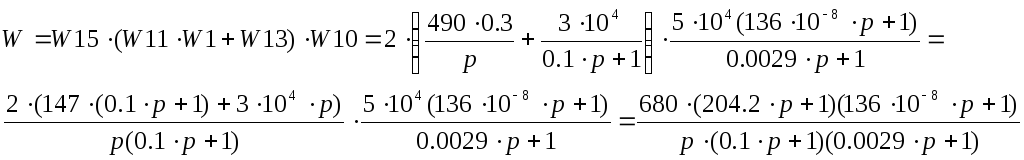
2.2 Определим устойчивость системы с помощью критерия Гурвица. Характеристическое уравнение найденной передаточной функции имеет вид:

0.00029p³+0.1029p²+p=0

Используя данное уравнение составим главный определитель Гурвица.

Из главного определителя выделим диагональные миноры:

То есть, система опять находится на границе устойчивости, так как главный определитель Гурвица равен нулю.

Проверим устойчивость системы по критерию Ляпунова. Для этого найдем корни характеристического полинома полученной передаточной функции.

Так как в результате получили два отрицательных корня и один нулевой, то, согласно критерию Ляпунова, можно сделать вывод, что система находится на границе устойчивости.

2.3 Построим переходный процесс линеаризованной системы.

- передаточная функция замкнутой системы.

По графику переходного процесса определим прямые оценки качества системы:

1. время переходного процесса t_п =0,007 c

2. время первого согласования t₁= 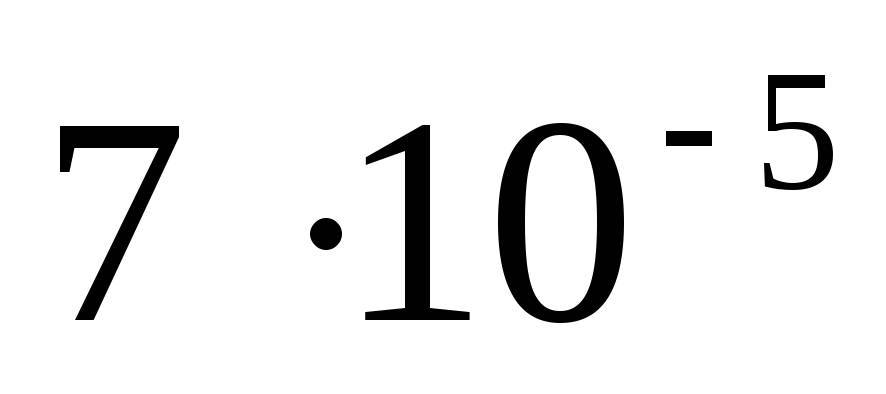c

3. установившееся значение h_уст =1

4. максимальное значение h_мах =1.9

5. перерегулирование

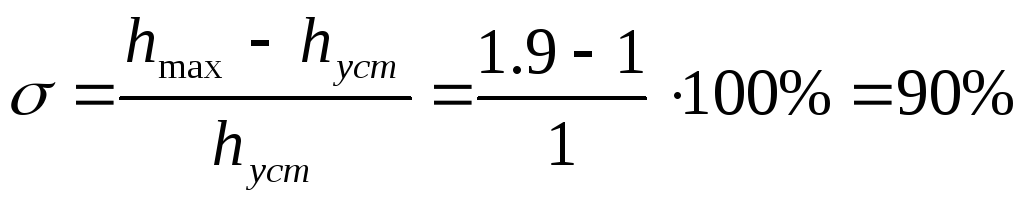
6. время нарастания регулируемой t_M=1.5

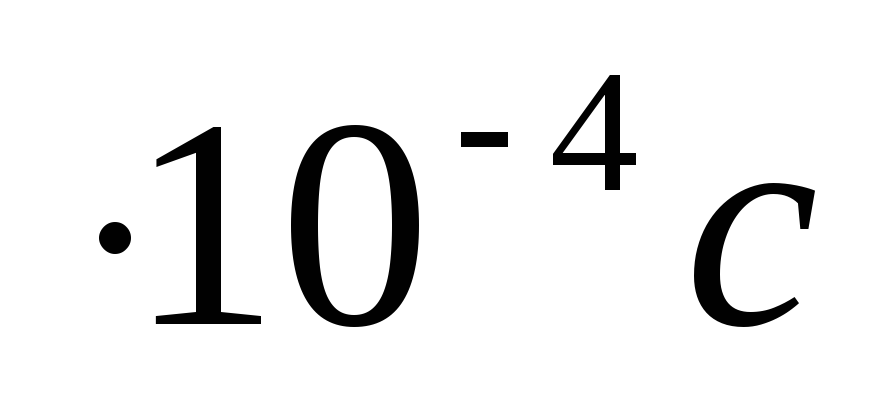
величины

2.4 Построим АЧХ и ФЧХ линеаризованной системы.

Заменим , получим:

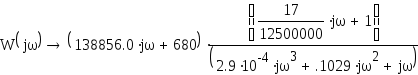
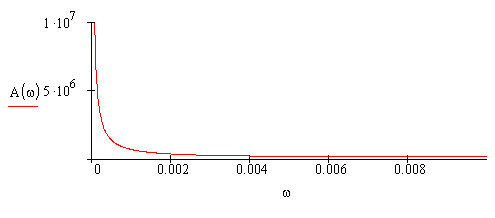
Найдем ФЧХ системы по формуле:

или

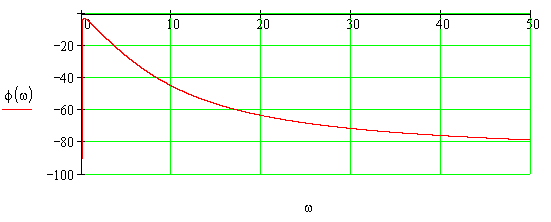
2.5 Построим ЛАЧХ и ЛФЧХ линеаризованной системы.

Определим собственные частоты каждого звена линеаризованной передаточной функции:

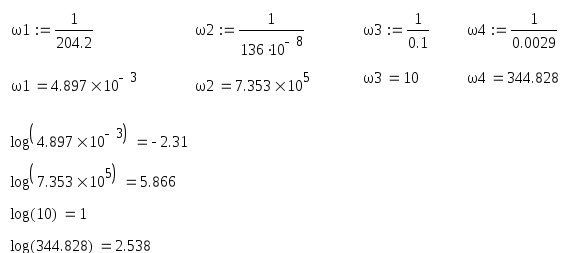
тогда

Построим график ЛФЧХ по функции:

или

Запас устойчивости по фазе: ψ=90°

Таким образом, можно сделать вывод, что звено W15=K существенно не повлияло на устойчивость системы, но при этом сократилось время переходного процесса, изменилась величина перерегулирования.