курсовая работа / tau-zibben-auf / r-TAU-kursovik-var-XX-4 / TAU_~1

11. Рассчитать реакцию РС на нетиповое воздействие

Необходимо рассчитать частотными методами реакцию РС на нетиповое входное воздействие при нулевых начальных воздействиях.

Не типовое воздействие на входе системы имеет вид:

Переходная характеристика при нетиповом воздействии:

12. Рассчитать последовательный регулятор

Необходимо рассчитать частотными методами передаточную функцию регулятора, так чтобы:

1. замкнутая система была устойчивой

2. длительность переходных процессов в 10 раз меньше, чем в разомкнутой системе без регулятора

3. перерегулирование не более 30 %

4. запасы устойчивости по амплитуде 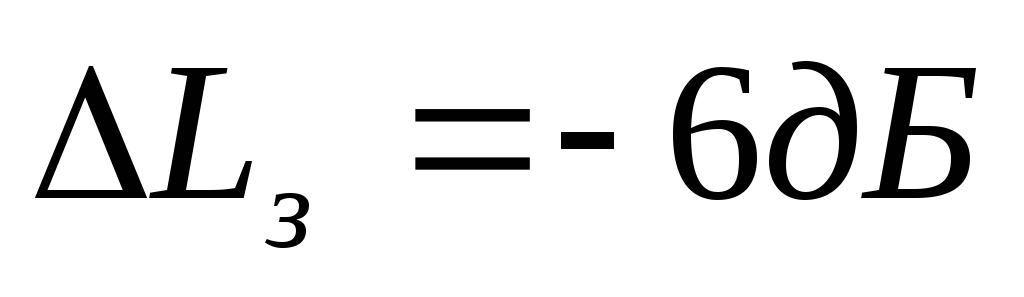и по фазе

Система с регулятором выглядит как:

R(s) – регулятор, который необходимо рассчитать.

, где

- передаточная функция желаемой системы

- передаточная функция разомкнутой реальной системы

Для расчета передаточной функции регулятора, сначала необходимо синтезировать желаемую передаточную функцию всей системы.

Построим желаемую ЛАЧХ.

Коэффициенты ошибок:

, так как мы строим систему с астатизмом первого порядка

Коэффициент усиления статической части желаемой системы:

Строим низкочастотную асимптоту желаемой ЛАЧХ с полученным коэффициентом усиления с наклоном –20 дБ/дек.

Желаемое время регулирования:

По номограммам для определяем , тогда

рад/с

Через точку проводим среднечастотную асимптоту с наклоном –20 дБ/дек.

По номограмме определяем , тогда границы средне частотного диапазона желаемой ЛАЧХ.

Так как низкочастотная и среднечастотная часть желаемой ЛАЧХ не пересекаются, то нужна сопрягающая часть с наклоном –40 дБ/дек, совместим ее правую границу с частотой сопряжения , это будет удовлетворять условию , тогда сопрягающая и среднечастотные части пересекаются на частоте

Также по условию границы среднечастотного диапазона желаемой ЛАЧХ выберем . Высокочастотная часть желаемой ЛАЧХ имеет наклон –40 дБ/дек.

Таким образом можно восстановить передаточную функцию желаемой системы:

Р ассчитаем реальные показатели полученной замкнутой системы:

1. Переходная характеристика:

и импульсная характеристика

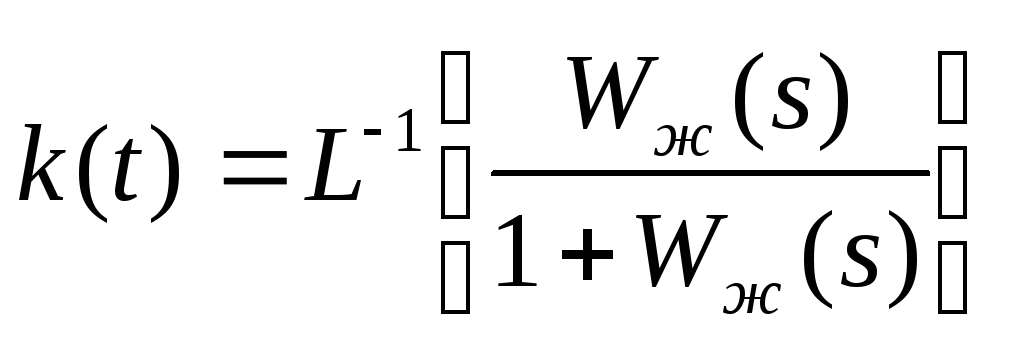
И меет апериодический характер, можно считать перерегулирование , быстродействие с. , это удовлетворяет условию и имеет нулевую статическую ошибку.

2. По ЛАЧХ и ЛФЧХ

проверим существование диапазона на границах которого один из запасов устойчивости обеспечивается точно:

исходя из этого, можно сказать , что желаемые запасы устойчивости в системе обеспечены.

3) ЛАЧХ и ЛФЧХ замкнутой системы с регулятором:

1 3. Синтезировать регулятор на ОУ

Вычислив ПФ последовательного регулятора получаем: