Вариант № 46

Структурная схема устройства

Где: ;

1.Получим частотные характеристики типовых звеньев

1.1.Апериодическое звено W4(10,1)

Обозначим его W41(S). Найдем ВЧХ, МЧХ, АЧХ, ФЧХ и построим ЛАЧХ, ЛФЧХ, АФЧХ.

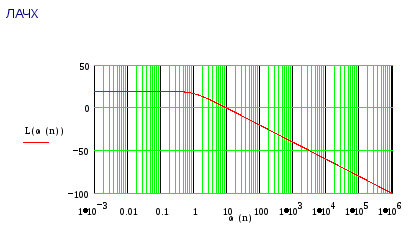
1.2.Апериодическое звено W4(1,10)

Обозначим его W42(S). Найдем ВЧХ, МЧХ, АЧХ, ФЧХ и построим ЛАЧХ, ЛФЧХ, АФЧХ.

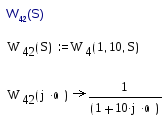
1.3.Форсирующее звено первого порядка W5(K,1)

Обозначим его W51(S). Найдем ВЧХ, МЧХ, АЧХ, ФЧХ и построим ЛАЧХ, ЛФЧХ, АФЧХ.

Пусть К=10

2.Получить ПФ для РС

Переходную функцию разомкнутой системы получим аналитическим методом.

В ыразив выход системы через ее вход , решив систему уравнений.

Подставив значения переходных характеристик звеньев системы получим:

3. Исследовать устойчивость РС от буквенного параметра методами Гурвица и Михайлова

3.1. Исследование устойчивости РС

по критерию Рауса-Гурвица

Исследуем устойчивость системы от параметра К.

Область устойчивости разомкнутой системы должна удовлетворять условиям:

г де - коэффициенты характеристического полинома , а -второй главный минор матрицы Гурвица.

Объединяя полученные решения, делаем вывод, что система устойчива при

3.2.Исследуем устойчивость РС по критерию Михайлова

При исследовании устойчивости РС от параметра К по критерию Михайлова используем комплексную частотную функцию характеристического полинома РС.

Для устойчивости РС с ХП третьей степени необходимо и достаточно выполнение условий:

Объединяя полученные решения, делаем вывод, что система устойчива при

Данный вывод полностью соответствует области устойчивости РС полученной методом Рауса-Гурвица.

4. ПФ замкнутой системы

Получим ПФ замкнутой единичной обратной связью системы.

5. Исследуем устойчивость ЗС .

У стойчивость ЗС необходимо исследовать от параметра К методами Гурвица-Рауса и Михайлова и получить диапазоны устойчивых и неустойчивых значений параметра в классе вещественных чисел.

5.1. Исследуем устойчивость ЗС

по критерию Рауса-Гурвица

Исследуем устойчивость от параметра К.

Область устойчивости замкнутой системы от значений К должна удовлетворять условиям.

Объединяя полученные решения, делаем вывод, что система устойчива при .

5.2. Исследуем устойчивость

по критерию Михайлова

При исследовании устойчивости ЗС от параметра К по критерию Михайлова используем комплексную частотную функцию характеристического полинома ЗС.

Для устойчивости РС с ХП третьей степени необходимо и достаточно выполнение условий:

Объединяя полученные решения, делаем вывод, что система устойчива при .

Данный вывод полностью соответствует области устойчивости ЗС полученной методом Рауса-Гурвица.

6. Сформировать набор значений параметра.

Набор значений параметра должен включать все граничные значения и по одному значению из каждого диапазона устойчивости и неустойчивости замкнутой системы.