Нижегородский государственный технический университет

КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Курсовая работа

ПО КУРСУ «ОСНОВЫ ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ».

Вариант 57

Выполнил Проверил

Студент гр.97-ВМ-2 преподаватель

Якунин А.В. Никулин Е.А.

2000

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ.

Произвести расчёт и исследовать схему, изображённую на рис.1 (вариант работы 57).

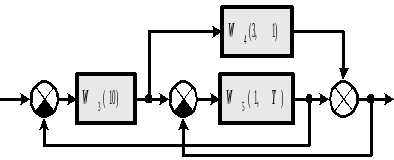
Рис.1

Где,

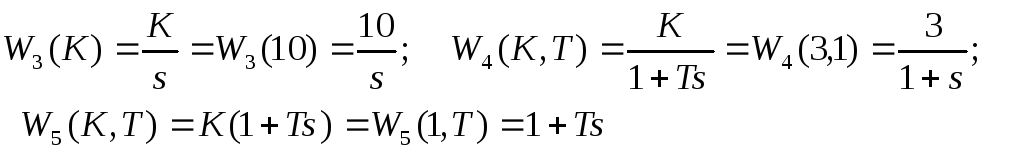
ВЫПОЛНЕНИЕ РАБОТЫ.

1. Построить все частотные характеристики блоков структурной схемы и принципиальные схемы моделирования блоков на операционных усилителях.

В соответствии с формулами для

(1.1)

(1.2)

(1.3)

(1.4)

Рассмотрим первое звено

С помощью Mathcad построим требуемые графики

_{Рис.2 Рис.3}

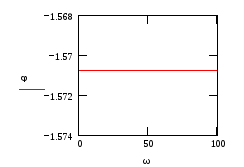
_{Рис.4 Рис.5}

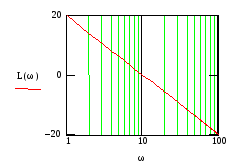
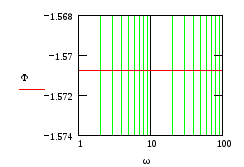
Рис.6 Рис.7

Рис.8

Составим для данной передаточной функции схему на ОУ.

Из таблицы 1.3 [1] перемножая элементы строки 2, столбцов б и в получаем:

Схема представлена на рис.9

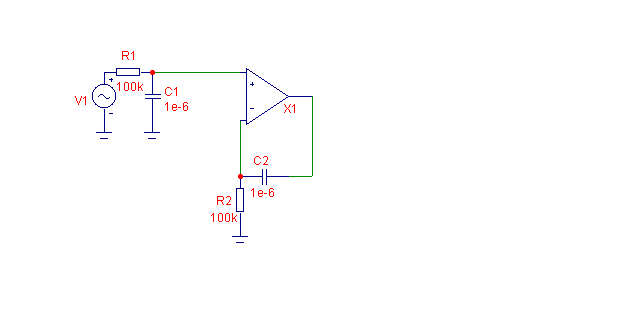
Рис.9

На рис.10 показаны ЛЧХ звена, полученные при моделировании в Micro-Cap

Рис.10

Рассмотрим второе звено.

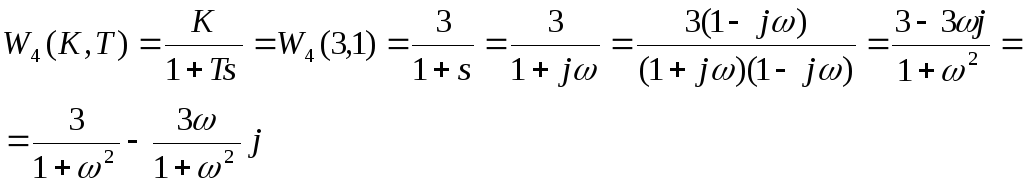
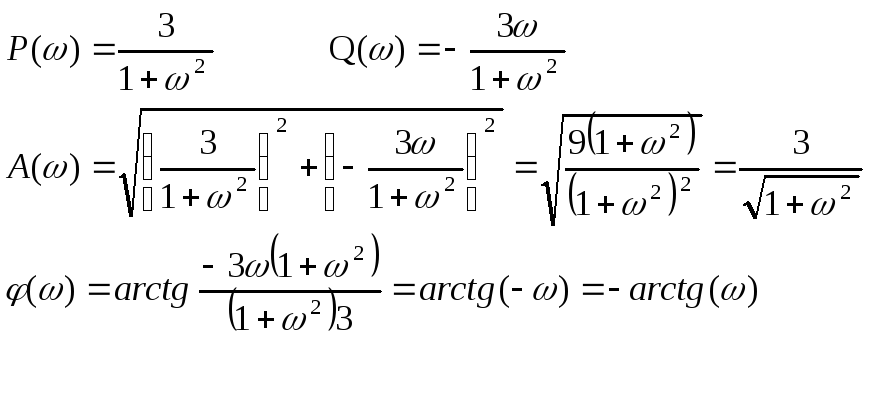
С помощью Mathcad построим требуемые графики

_{Рис.11 Рис.12}

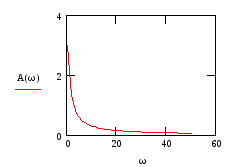
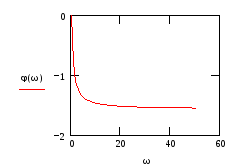
Рис.13 Рис.14

_{Рис.15 Рис.16}

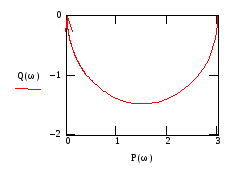
_Рис.17

Составим для данной передаточной функции схему на ОУ.

Из таблицы 1.3 [1] перемножая элементы строки 2, столбца б и строки 1, столбца в получаем:

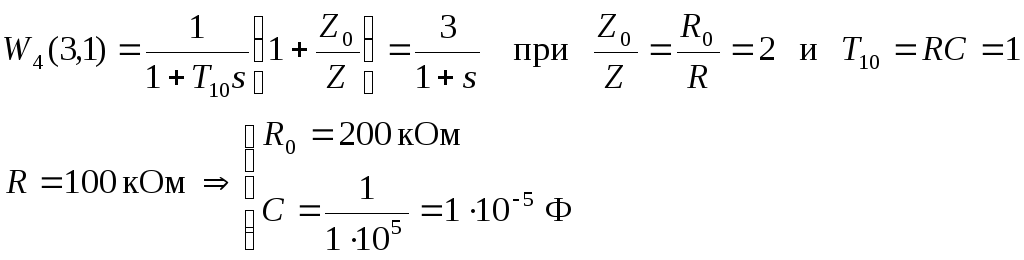
Схема представлена на рис.18

_Рис.18

На рис.19 показаны ЛЧХ звена, полученные при моделировании в Micro-Cap

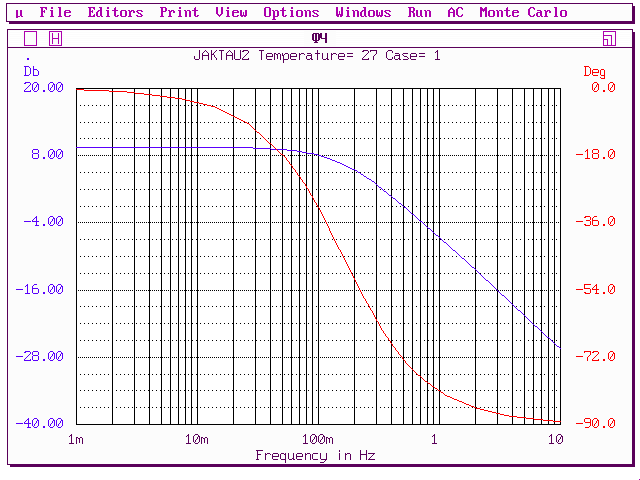_Рис.19

_{Рассмотрим третье звено.}

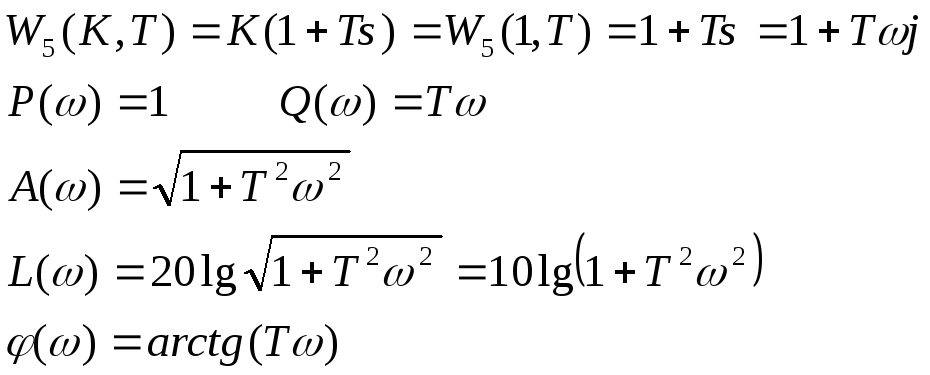
С помощью Mathcad построим требуемые графики при различных значениях T

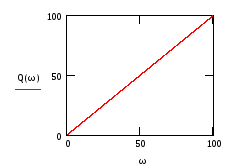
Рис.20 Рис.21

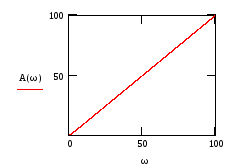
Рис.22 Рис.23

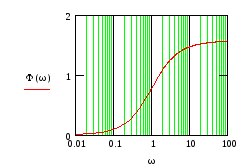
_{Рис.24 Рис.25}

_Рис.26

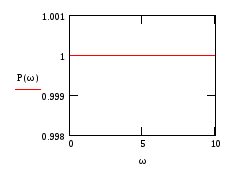
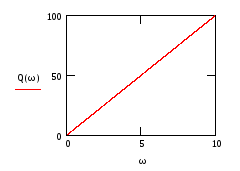
Рис.27 Рис.28

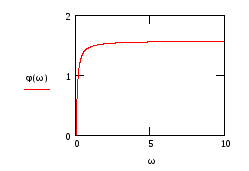
_{Рис.29 Рис.30}

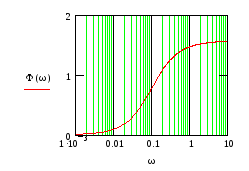
_{Рис.31 Рис.32}

_Рис.33

_{Рис.34 Рис.35}

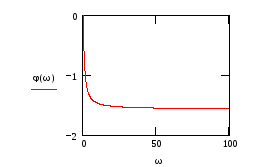
_{Рис.36 Рис.37}

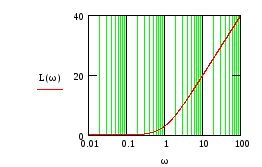
_{Рис.38 Рис.39}

_Рис.40

Составим для данной передаточной функции схему на ОУ.

Из таблицы 1.3 [1] в соответствии со строкой 3, столбцом в имеем:

Схема представлена на рис.41

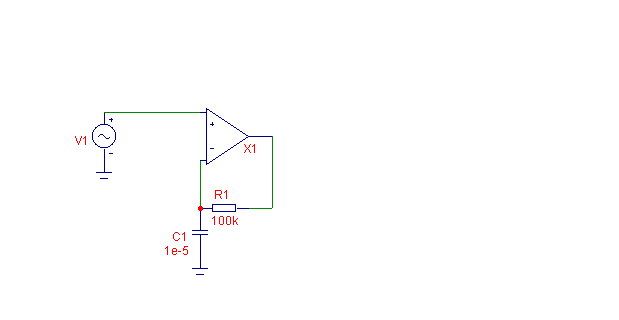
_Рис.41

Ниже показаны ЛЧХ звена при значениях параметра Т=1 (рис.42 а) и Т=10 (рис.42 б), полученные при моделировании в Micro-Cap. В качестве примера в таблице 1.1 приведены значения амплитуды и фазы при различных значениях частоты, соответствующие значению Т=1, а на рис.42 в, г, д – входной и выходной сигналы для каждой из частот, представленных в этой таблице (рис.42 в – f = 0.015 Гц; рис.42 г – f = 0.15 Гц; рис.42 д – f = 1.5 Гц ). Таблица 1.1.

	0	3	20
	1	1.4	10
	6	45	84

Рис.42 а

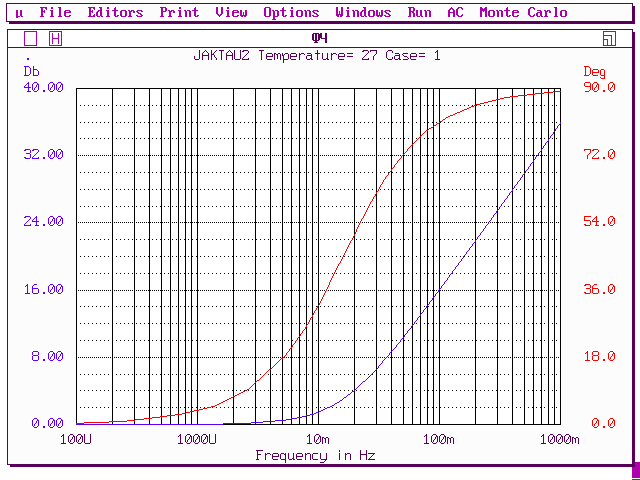Рис.42 б

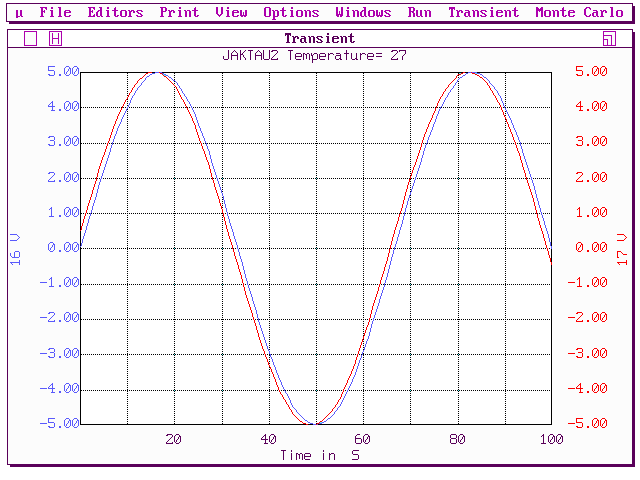Рис.42 в

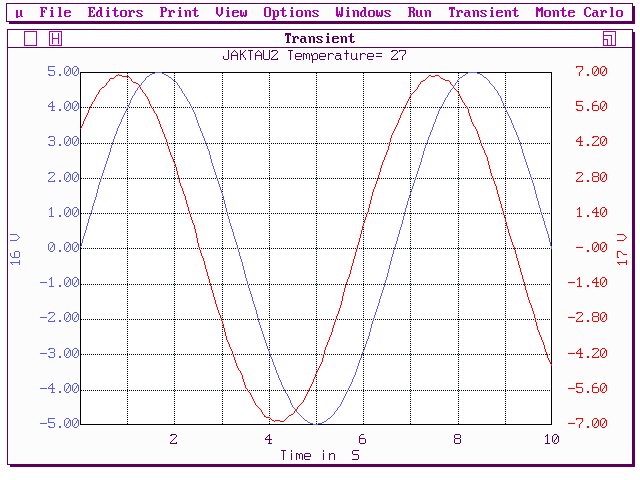Рис. 42 г

Рис. 42 д

2. Получить ПФ разомкнутой системы (РС).

Метод структурных преобразований.

_Y1

_X

X1 Y2 Y

_Рис.43

_Рис.44

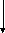
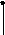
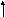
_Рис.45

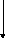
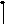
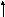
_Рис.46

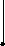
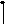
_Рис.47

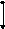
_Рис.48

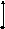
Рис.49

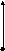
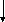
Рис.50

Рис.51 Рис.52 Рис.53 Рис.54

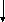_Рис.55

Рис.56

_{Упростим схему, изображённую на рис.43 с помощью алгебраических преобразований.}

3. Исследовать устойчивость РС от буквенного параметра методами Гурвица и Михайлова.

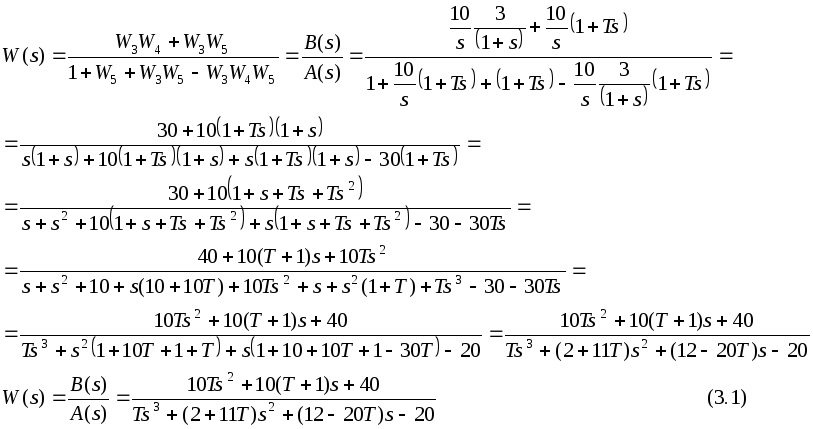_{Характеристический полином (ХП) в разомкнутой системе имеет вид:}

_{Метод Гурвица}

_{Составим матрицу Гурвица}

Для ХП третьей степени необходимые и достаточные условия устойчивости имеют вид

_{Получаем систему}

_{-0.18 -0.16 0.67 T}

_Рис.57

_{Из рисунка видно, что система решений не имеет. Следовательно, разомкнутая система неустойчива при любом Т.}

_{Метод Михайлова .}

_{ХП имеет вид (3.2) . Заменяя в нём получим:}

_{Действительная часть:}

_{Мнимая часть:}

_{В соответствии с критерием Михайлова должно быть:}

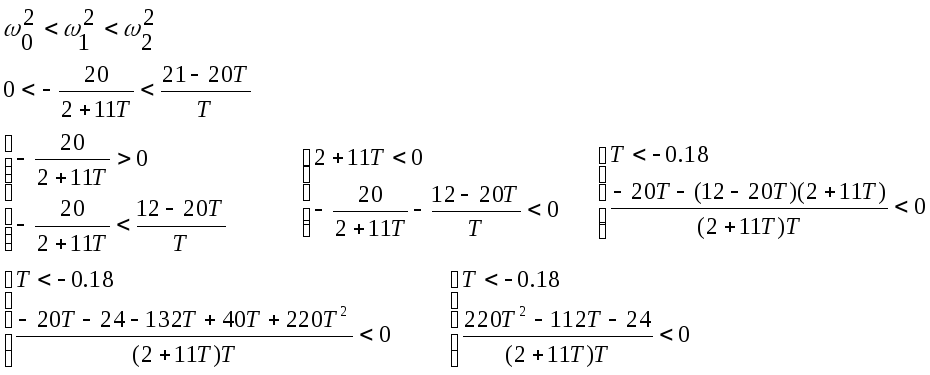_{Учитывая, что имеем . Следовательно, наша система принимает вид:}

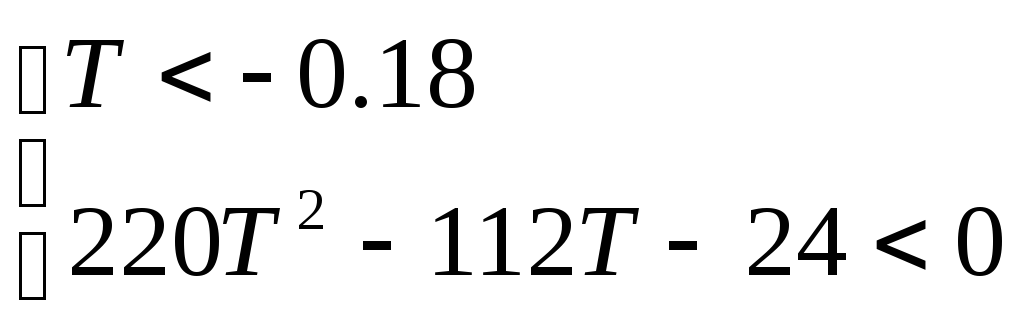
_{Корни уравнения (см.(3.3))}

_{Окончательно получаем систему, сходную с (3.4) и делаем вывод, что разомкнутая система не имеет областей устойчивости .}

Построим годографы Михайлова разомкнутой системы для значений Т= -1; 0; 1; 2.1; 10. Для этого значения Т подставляем в мнимую и действительную части ХП, полученного в начале пункта. Построение производим с помощью MathCad.

_Рис.58

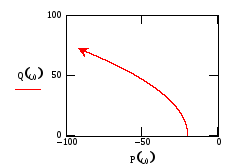
_Рис.59

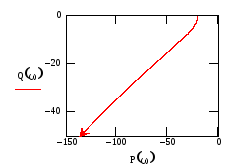
_Рис.60

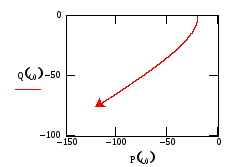
_Рис.61

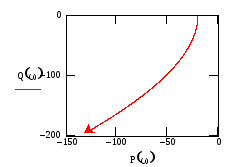
_Рис.62

_{Из рис.59-62 видно, что изменение аргумента годографа её ХП третьей степени составляет всего один квадрант. Следовательно, при всех выбранных значениях Т разомкнутая система является неустойчивой. Система рис.58 также неустойчива, поскольку годограф вращается по часовой стрелке и проходит через два квадранта.}

4. Получить ПФ замкнутой единичной отрицательной обратной связью системы (ЗС).

Рис.63

_{Передаточная функция разомкнутой системы имеет вид (3.1). Вычислим функцию замкнутой системы.}

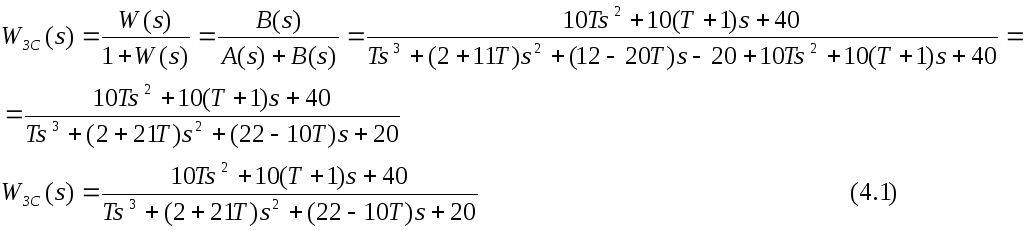_{ХП замкнутой системы имеет вид:}

_{Коэффициенты полинома}

5. Исследовать устойчивость ЗС от буквенного параметра методами Гурвица и Рауса и получить диапазоны устойчивых и неустойчивых значений параметра в классе вещественных чисел.

Метод Гурвица.

_{Составим матрицу Гурвица}

Для ХП третьей степени необходимые и достаточные условия устойчивости имеют вид

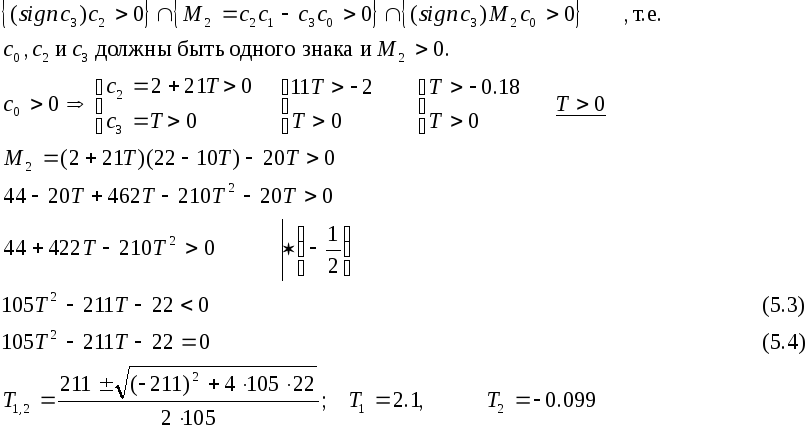
_{Получаем систему}

-0.099 0 2.1 Т Рис.64

Из рис.64 видно, что замкнутая система устойчива в интервале 0<T<2.1 .

Метод Рауса.

Строим таблицу Рауса:

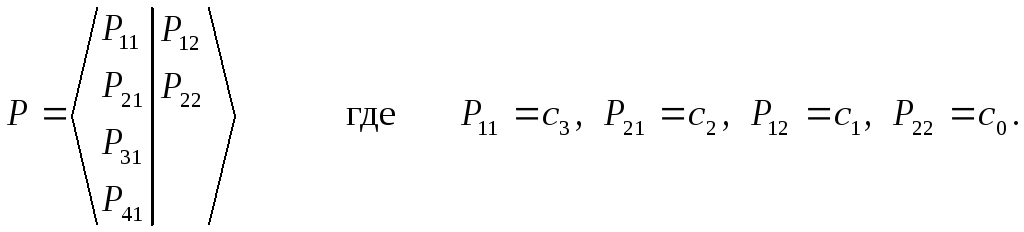
Остальные Р находим по формуле:

Далее, подставляя коэффициенты ХП, имеем:

Критерием устойчивости действительного полинома является постоянство знаков всех элементов первого столбца таблицы Рауса. Так как 20>0, получаем систему:

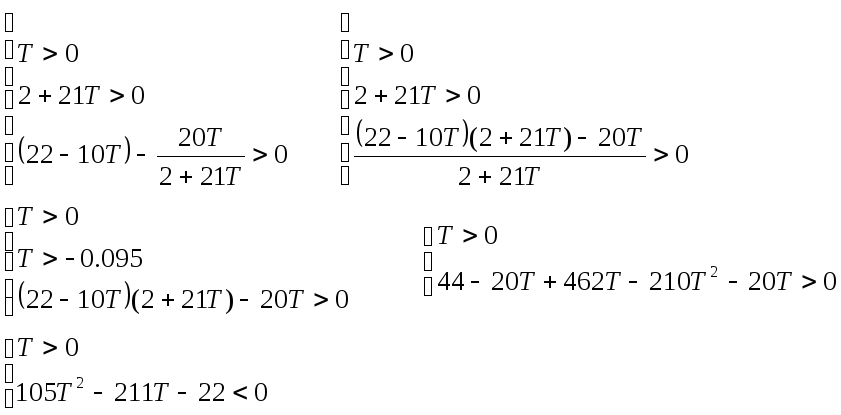
Нижнее неравенство сходно с (5.3) и его решением является

Таким образом, наша система приобретает вид (5.5). Следовательно, опираясь на рис.64, делаем вывод об устойчивости замкнутой системы на интервале 0<T<2.1.

6. Сформировать набор значений параметра, включающий все граничные значения и по одному значению из каждого диапазона устойчивости и неустойчивости ЗС.

0 2.1 T

Рис.65

На рис.65 штриховкой показан диапазон значений Т , при которых замкнутая система является устойчивой. Для дальнейшей работы выбираем следующие значения параметра : Т= -1, Т= 10 (ЗС неустойчива); Т=0, Т= 2.1 (границы устойчивости ЗС) и Т=1 (ЗС устойчива).

7. Для каждого значения параметра из набора построить частотные характеристики, необходимые для исследования устойчивости ЗС от параметра по критериям Найквиста и Михайлова.

7.1 Устойчивость по критерию Михайлова.

7.1.1. Из рис.58 видно, что при Т=-1 годограф ХП РС имеет изменение аргумента –2 квадранта, что соответствует числу правых корней .

7.1.2. Из рис.59 видно, что при Т=0 годограф ХП РС имеет изменение аргумента –1 квадрант, что соответствует числу правых корней .

7.1.3. Из рис.60-62 видно, что при Т=1, 2.1, 10 годограф ХП РС имеет изменение аргумента 1 квадрант, что соответствует числу правых корней .

7.2 Исследование устойчивости по критерию Найквиста.

Рассмотрим систему, образованную замыканием объекта с ПФ W(s) контуром единичной ООС. Замкнутая система имеет ХП вида (4.2) и ПФ вида (4.1)

Х У Хо Рис.66

_{Временно разорвём ООС в точке Хо и определим контурные ПФ и ХП разомкнутого контура.}

_{Подставляем значение Т в выражение разомкнутой ПФ (3.1).}

_{7.2.1. Т= -1}

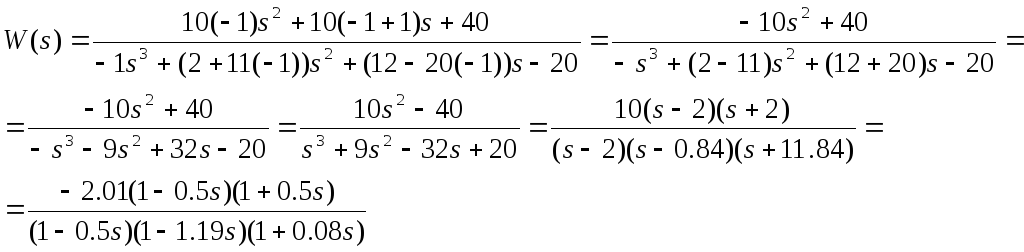
_{Элементарные типовые звенья и их характеристики:}

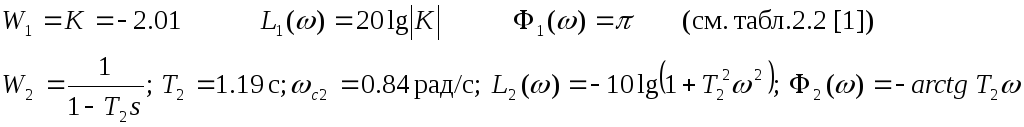
_{На рис.67-70 представлены ЛЧХ каждого звена и результирующие ЛАЧХ и ЛФЧХ всей ПФ.}

_Рис.67

_Рис.68

_Рис.69

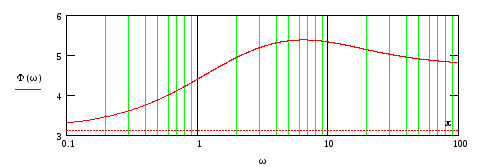
_Рис.70

_{Из рис.58 видно, что ХП разомкнутой системы имеет правых корня. На интервале частот, где ,число пересечений граничных уровней фазы равно , что не тождественно отношению . Следовательно, исходя из логарифмического критерия Найквиста, делаем вывод об неустойчивости ЗС с контурной ПФ (7.1). РС также неустойчива, т.к. ЛФЧХ стремится к граничному уровню на интервале положительной ЛАЧХ.}

_{Получим АЧХ системы и построим годографы контурной ПФ в полярной (рис.71) и декартовой (рис.72) системе координат.}

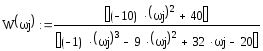
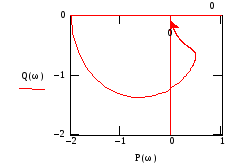
_{Рис.71 Рис.72}

_{Видно , что годограф разомкнутого контура пересекает действительную ось левее точки раза, а должен был бы пересечь раз. Отсюда , в соответствии с частотным критерием Найквиста, делаем вывод об неустойчивости ЗС.}

_{7.2.2. Т= 0}

_{Элементарные типовые звенья и их характеристики:}

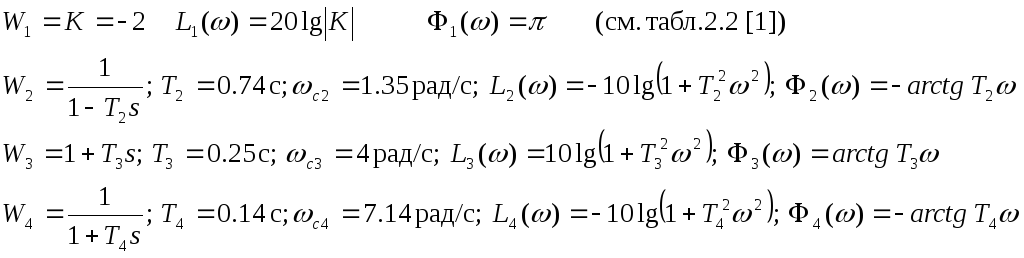
_{На рис.73-76 представлены ЛЧХ каждого звена и результирующие ЛАЧХ и ЛФЧХ всей ПФ.}

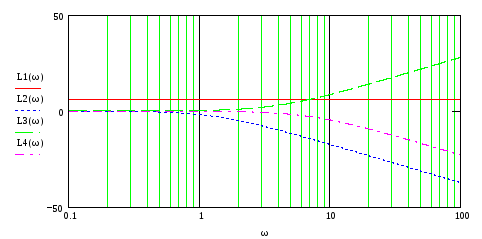
_Рис.73

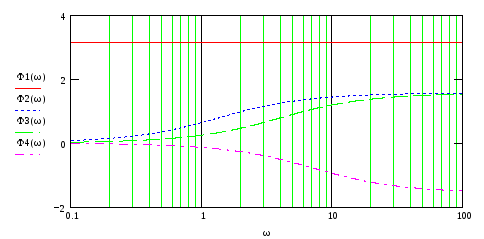
_Рис.74

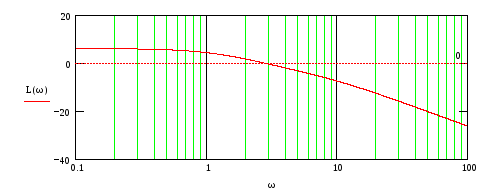
_Рис.75

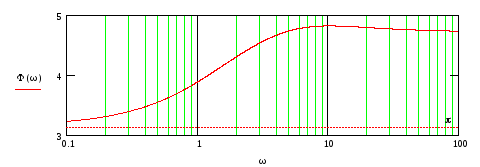
_Рис.76

_{Из рис.59 видно, что ХП разомкнутой системы имеет правый корень. На интервале частот, где ,число пересечений граничных уровней фазы равно , что тождественно отношению . Следовательно, исходя из логарифмического критерия Найквиста, делаем вывод об устойчивости ЗС с контурной ПФ (7.1). РС неустойчива, т.к. ЛФЧХ стремится к граничному уровню на интервале положительной ЛАЧХ.}

_{Получим АЧХ системы и построим годографы контурной ПФ в полярной (рис.77) и декартовой (рис.78) системе координат.}

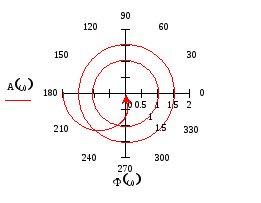
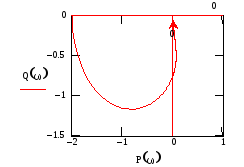
_{Рис.77 Рис.78}

_{Видно , что годограф разомкнутого контура пересекает действительную ось левее точки раза, а должен был бы пересечь раза. Отсюда, в соответствии с частотным критерием Найквиста, делаем вывод об устойчивости ЗС.}

_{7.2.3. Т= 1}

_{Элементарные типовые звенья и их характеристики:}

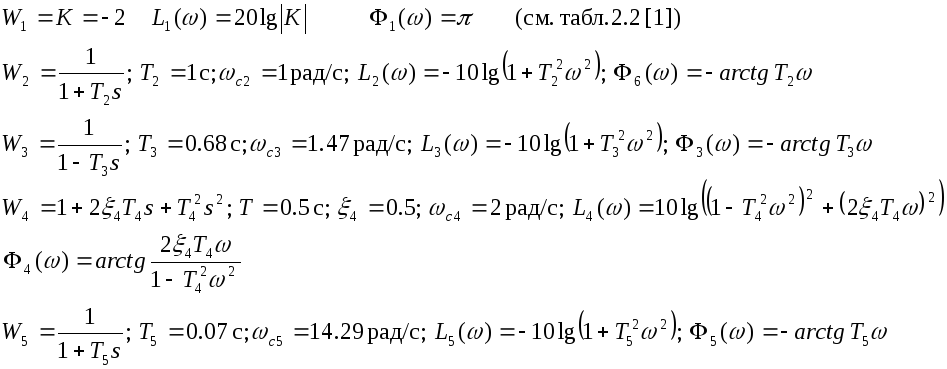
_{На рис.79-82 представлены ЛЧХ каждого звена и результирующие ЛАЧХ и ЛФЧХ всей ПФ.}

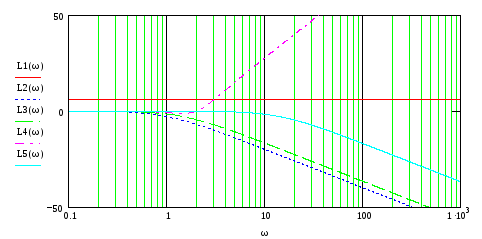
_Рис.79

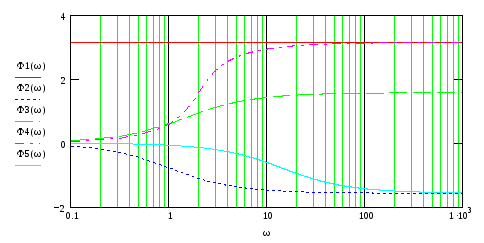
_Рис.80

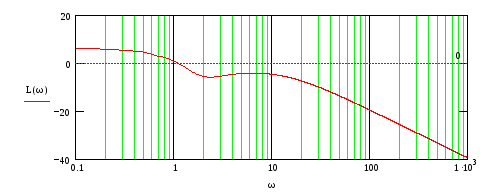
_Рис.81

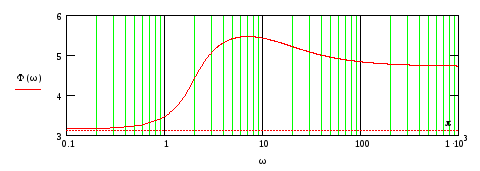
_Рис.82

_{Из рис.60 видно, что ХП разомкнутой системы имеет правый корень. На интервале частот, где ,число пересечений граничных уровней фазы равно , что тождественно отношению . Следовательно, исходя из логарифмического критерия Найквиста, делаем вывод об устойчивости ЗС с контурной ПФ (7.1). РС неустойчива, т.к. на интервале положительной ЛАЧХ сумма переходов ЛФЧХ через граничные уровни составляет .}

_{Получим АЧХ системы и построим годографы контурной ПФ в полярной (рис.83) и декартовой (рис.84) системе координат.}

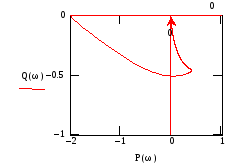
_{Рис.83 Рис.84}

_{Видно , что годограф разомкнутого контура пересекает действительную ось левее точки раза, а должен был бы пересечь раза. Отсюда делаем вывод об устойчивости ЗС.}

_{7.2.4. Т= 2.1}

_{Элементарные типовые звенья и их характеристики:}

_{На рис.85-88 представлены ЛЧХ каждого звена и результирующие ЛАЧХ и ЛФЧХ всей ПФ.}

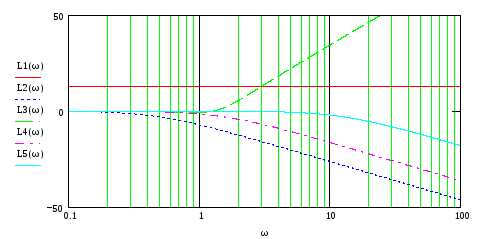
_Рис.85

_Рис.86

_Рис.87

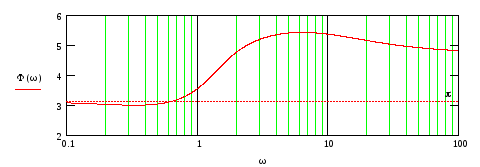
_Рис.88

_{Из рис.61 видно, что ХП разомкнутой системы имеет правый корень. На интервале частот, где ,число пересечений граничных уровней фазы равно , что тождественно отношению . Следовательно, исходя из логарифмического критерия Найквиста, делаем вывод об устойчивости ЗС с контурной ПФ (7.1). РС неустойчива, т.к. на интервале положительной ЛАЧХ сумма переходов ЛФЧХ через граничные уровни составляет .}

_{Построим годограф контурной ПФ.}

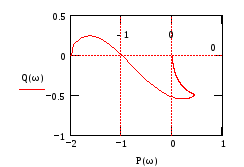
_Рис.89

_{В данном случае ЗС находится на границе устойчивости (нейтральна), т.к. годограф проходит через точку и при уменьшении параметра Т система становится устойчивой (число переходов левее точки Найквиста равно и отношение ).}

_{7.2.5. Т= 10}

_{Элементарные типовые звенья и их характеристики:}

_{На рис.90-93 представлены ЛЧХ каждого звена и результирующие ЛАЧХ и ЛФЧХ всей ПФ.}

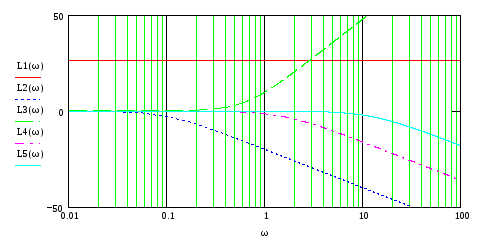
_Рис.90

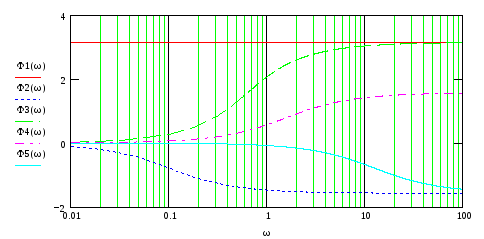
_Рис.91

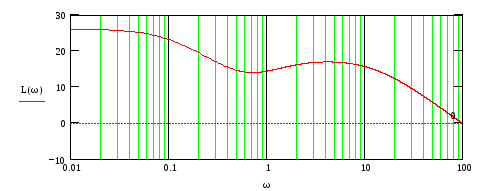
_Рис.92

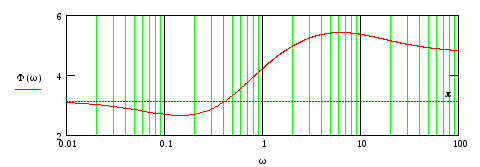
_Рис.93

_{Из рис.62 видно, что ХП разомкнутой системы имеет правый корень. На интервале частот, где ,число пересечений граничных уровней фазы равно 1, что не тождественно отношению . Следовательно, исходя из логарифмического критерия Найквиста, делаем вывод об неустойчивости ЗС с контурной ПФ (7.1). РС неустойчива, т.к. на интервале положительной ЛАЧХ сумма переходов ЛФЧХ через граничные уровни составляет 1 .}

_{Построим годограф контурной ПФ.}

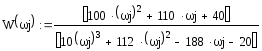
_Рис.94

Видно , что годограф разомкнутого контура (контурной ПФ) пересекает действительную ось левее точки раза, а должен был бы пересечь раза. Отсюда делаем вывод об неустойчивости ЗС.

8. Выбрать из набора параметров значение, при котором РС устойчива, получить числовую ПФ системы с этим параметром и построить каноническую схему моделирования РС на ОУ.

Т.к. РС не имеет областей устойчивости, принимаем значение Т = 1 в (3.1) и получаем значение ПФ.

Рис. 95

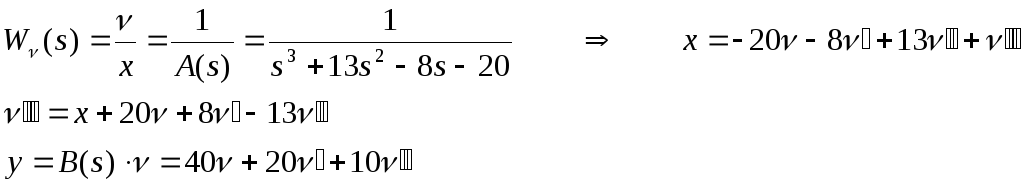
Построим каноническую схему

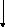
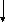
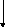
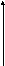
Рис. 96

На рис.97, 98 приведена электрическая схема ПФ и её ЛЧХ, полученные при моделировании в Micro-Cap, а также реакция системы на импульсное (ударное)(рис.98 б) и единичное (ступенчатое) (рис. 98 в,г) воздействия.

Рис.97

Ниже приведён расчёт элементов схемы.

Интеграторы на ОУ Х2-Х4 имеют следующие параметры элементов:

Рассмотрим сумматор на ОУ Х1.

Рассмотрим сумматор на ОУ Х5.

На рис. 98 а представлены ЛЧХ схемы на ОУ. Рис. 98 б иллюстрирует реакцию системы на импульс длительностью одна микросекунда и амплитудой один мегавольт. Рис.98 в, г демонстрируют то, как система реагирует на единичное (ступенчатое) воздействие (и -импульс, и ступенька начинаются в момент времени, равный пяти миллисекундам).

Рис.98 а

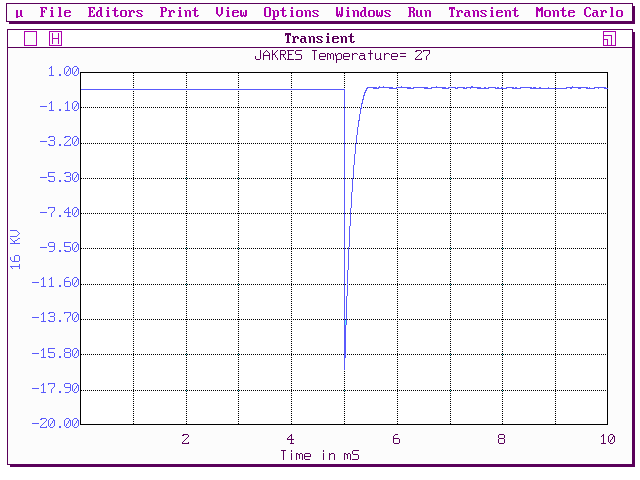Рис.98 б

Рис.98 в

Рис.98 г

9. Получить оценки качества временных характеристик РС спектральными и частотными методами.

По (3.1) со значением параметра Т=1 получаем ПФ РС

(9.1)

Полюса ПФ: .

Нули ПФ: .

Корни ПФ изображены на рис.98.

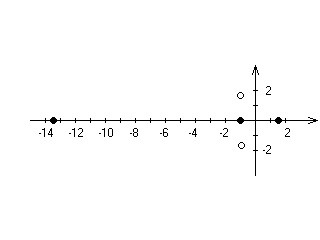
Рис. 98.

9.1. Спектральные оценки качества переходного процесса.

Основные спектральные параметры:

• Степень устойчивости 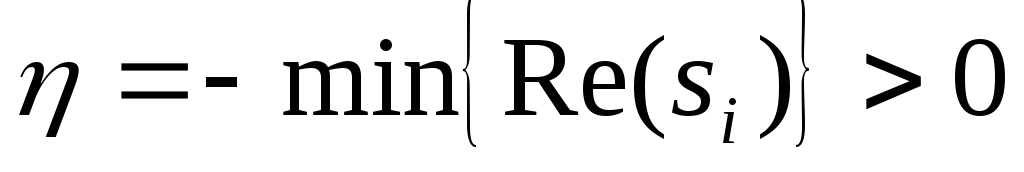- расстояние от мнимой оси до ближайшего левого полюса ПФ.

• Степень быстродействия 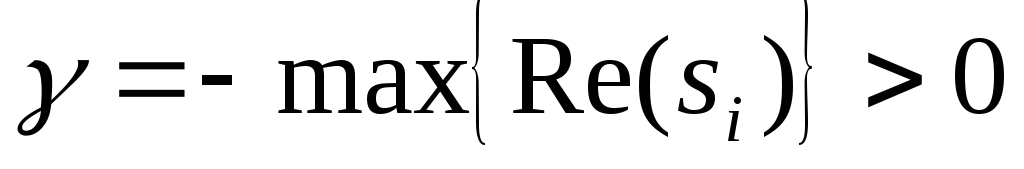- расстояние от мнимой оси до наиболее удалённого левого полюса ПФ. .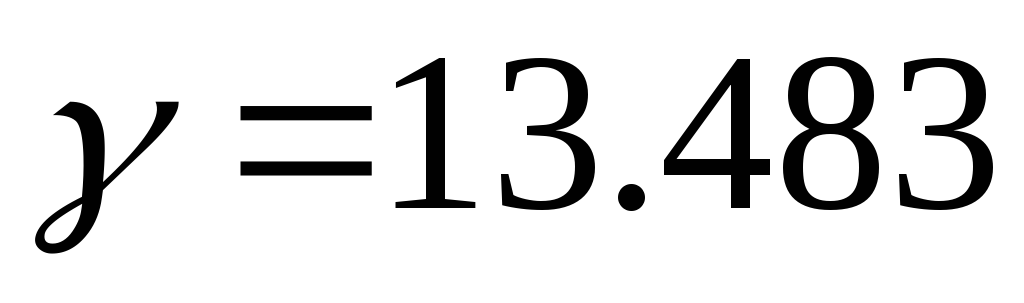

• Степень жёсткости . Система является жёсткой.

• Степень колебательности - тангенс угла  раствора для ближайших к мнимой оси левых комплексных полюсов.

Основные спектральные оценки качества:

• Время регулирования . .

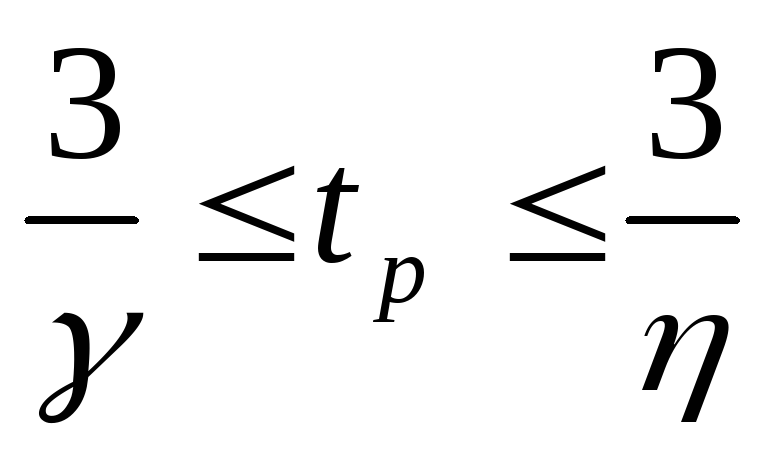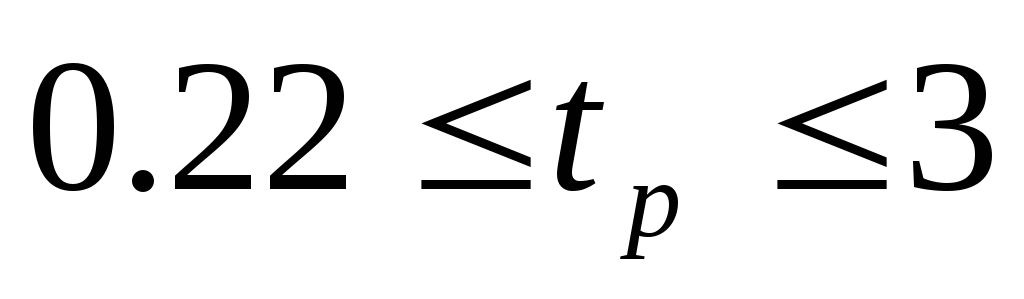• Верхняя оценка перерегулирования . .

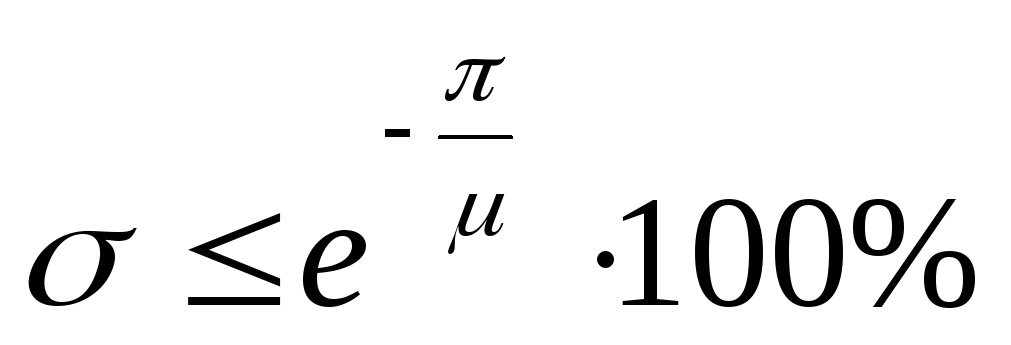• Степень затухания .

• Число колебаний .

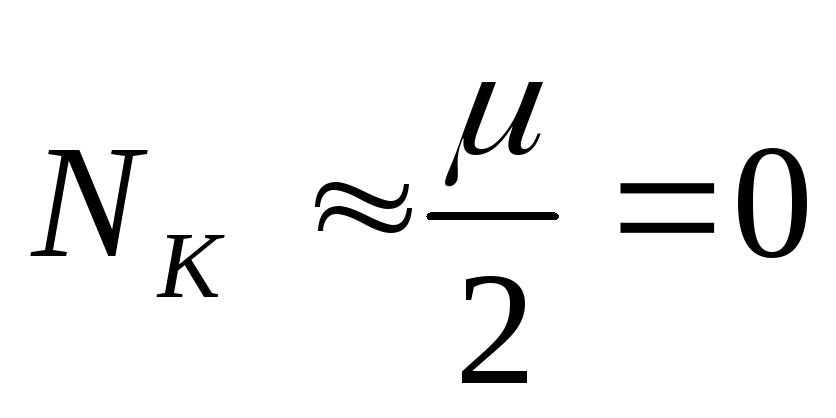9.2. Частотные оценки качества переходного процесса.

Получим ВЧХ ПФ, заменяя в (9.1) s на j .

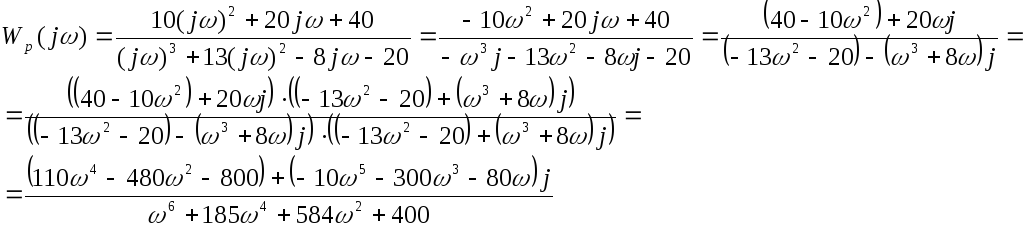Отсюда получаем ВЧХ

(9.2)

На рис.99, 101, 102 представлены графики этой характеристики. Рис.100 показывает положение первой точки перегиба (выпуклости \ вогнутости) ВЧХ.

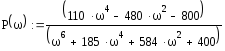
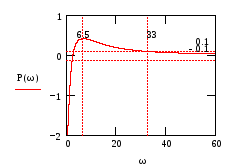
_Рис.99

_Рис.100

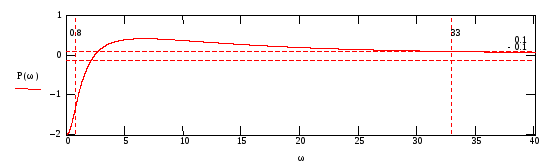
Рис. 101

Рис.102

• Начальное значение ПХ .

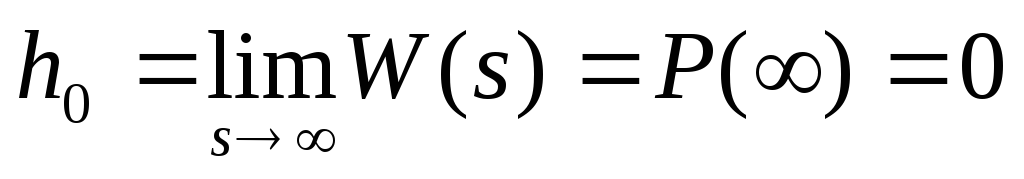• Установившееся значение ПХ .

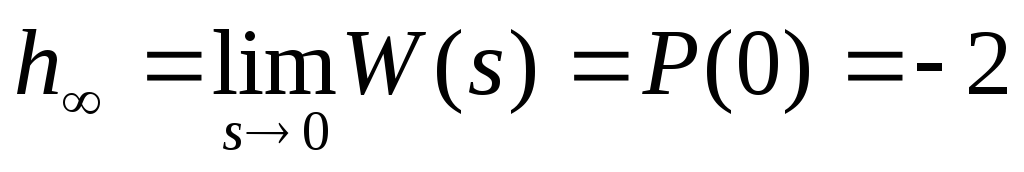• Время регулирования :

По частоте полосы пропускания ВЧХ (рис. 101) : получаем нижнюю границу времени регулирования

.

По частоте первого резкого перегиба ВЧХ (рис. 100, 101) получаем верхнюю границу времени регулирования .

Т. о. .

• Оценка перерегулирования. Т. к. ВЧХ имеет , то ПХ удовлетворяет условию .

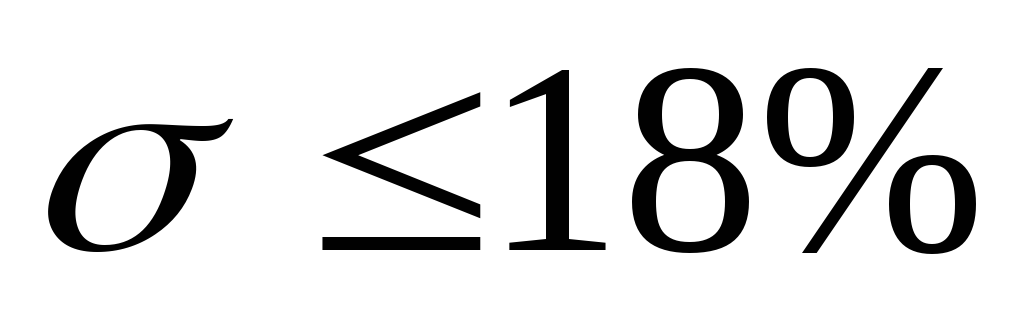• Оценки параметров колебаний ПХ

Коэффициент резонанса на частоте (рис. 102).

Коэффициент демпфирования

Частота колебаний ; Гц .

Постоянная времени с .

Показатель затухания колебаний .

Степень колебательности .

Т.к. комплексные полюсы ПФ не являются доминирующими в её спектре, то резонансный пик ВЧХ располагается в среднечастотной области. Оценки параметров колебаний являются слишком грубыми.

Полученные показатели сведены в таблицу.

Таблица 9.1.

Показатель	Спектральные оценки	Частотные оценки
Степень устойчивости 	1
Степень быстродействия 	13.483
Степень жёсткости r	13.483
Степень колебательности 	0
Время регулирования
Перерегулирование
Степень затухания 	1
Число колебаний	0	0
Начальное значение ПХ		0
Установившееся значение ПХ		-2

10 Рассчитать частотными методами временные характеристики РС, построить их графики и сравнить показатели качества с оценками из пункта 9.

10.1. Импульсная характеристика w(t).

Формула разложения Хевисайда для данной характеристики имеет вид:

(10.1)

, где - корни полинома A(s); - кратность i-го корня; - ПФ РС (см. 9.1).

Т.к. в нашем случае все полюса действительные с кратностью 1, то формула получения импульсной характеристики значительно упрощается:

(10.2)

Окончательно получаем:

(10.3)

График ИХ представлен на рис.103

_Рис.103

Рис. 104

График на рис.103 иллюстрирует неустойчивость системы. Пунктиром на графике рис.103 и отдельно на рис.104 изображена ИХ без расходящейся составляющей .

10.2. Переходная характеристика h(t).

ПХ находим с помощью таблицы преобразования Лапласа.

(10.4)

,где - обратное преобразование Лапласа.

Разложим выражение в фигурных скобках на слагаемые:

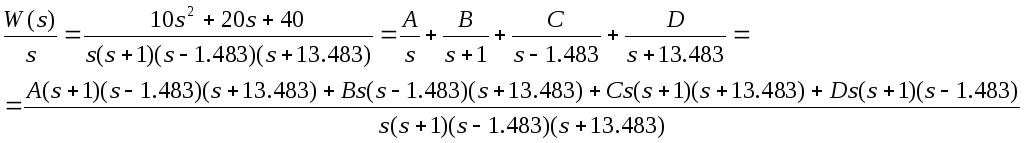
Получаем:

ПХ имеет вид:

(10.5)

На рис.105 представлен график ПХ.

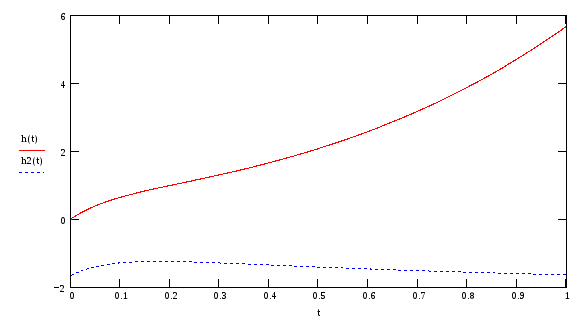
_Рис.105

Рис.106

Начальное значение h(0) совпадает c оценкой пункта 9. Оценка установившегося значения расходящейся ПХ некорректна, т.к. её ПФ имеет правый полюс s=1.483 . График h(t) на рис.105 иллюстрирует неустойчивость системы. Пунктиром на рис.105 и отдельно на рис.106 изображена ПХ без расходящейся составляющей .

11. Рассчитать реакцию РС на нетиповое входное воздействие при нулевых начальных условиях, построить графики входного и выходного сигналов.