
- •Механика
- •Раздел 1. Введение
- •Раздел 2. Кинематика
- •Векторная система отсчета
- •Декартова система отсчета
- •Цилиндрическая или полярная система отсчета
- •Раздел 3. Законы динамики
- •Раздел 4. Законы сохранения
- •Раздел 5. Гравитационное поле
- •Раздел 6. Движение в неинерциальных системах отсчета
- •Раздел 7. Элементы теории относительности. Примеры.
Раздел 5. Гравитационное поле
Закон всемирного тяготения. Гравитационное поле. Гравитационная энергия. Гравитационный радиус. “Черные дыры”. Движение в поле тяготения Земли. Космические скорости.
Законы Кеплера:
-
все планеты вертятся по эллипсу, в одном из фокусов которого Солнце.
-
за любые равные промежутки времени радиус-вектор планеты описывает одинаковую площадь то есть

-
отношение квадратов периода вращения планет к кубу длин больших полуосей одинаков для всех планет:
 .
.
Законы
Кеплера
 Закон всемирного тяготения.
Закон всемирного тяготения.
Предположим,
что все орбиты круговые и так как
 – это касательная к траектории, то
– это касательная к траектории, то
 .
.
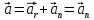 ,
где
,
где
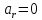 ,
так как
,
так как
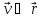


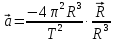 ,
где
,
где

согласно третьему закону Кеплера.
Таким
образом



 .
По
третьему закону Ньютона:
.
По
третьему закону Ньютона:
 .
Следовательно
.
Следовательно
 .
Таким
образом,
.
Таким
образом,
 =>
=>

Ньютон
предположил, что
 ,
где
,
где
 - гравитационная постоянная.
- гравитационная постоянная.
Таким
образом,
 – закон тяготения между планетами
солнца.
– закон тяготения между планетами
солнца.
 – закон
всемирного тяготения.
– закон
всемирного тяготения.
Эта сила прямо пропорциональна произведению их масс, и обратно пропорциональна квадрату расстояний между ними.
Особенности:
 ,
,

Таким
образом, для небольших высот
 ,
тогда
,
тогда
 ,
где
,
где

 ,
,
С
точностью


 решим,
что
решим,
что

Принцип эквивалентности масс:
Если
есть система, двигающаяся с ускорением
 и находящаяся в гравитационном поле,
то исследователь, находящийся в этой
системе, не может определить, какая
часть сил обусловлена силами тяжести,
а какая – ускоренным движением системы.
и находящаяся в гравитационном поле,
то исследователь, находящийся в этой
системе, не может определить, какая
часть сил обусловлена силами тяжести,
а какая – ускоренным движением системы.
-
Масса гравитации =

-
Эти силы
 и
и
 носят характер притяжения.
носят характер притяжения. -

Таким
образом,
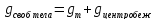


Полевая теория
Любое тело создает вокруг себя поле – гравитационное поле.
Свойства гравитационного поля:
-
Оно непрерывно распределено в пространстве, проникает в другие поля и вещества.
-
Это поле действует с неокторой силой на все тела, помещенные в это поле.


Напряженность
гравитационного поля


-
 планету
можно заменить точечным телом с такой
же массой M.
планету
можно заменить точечным телом с такой
же массой M. -
Это поле цетральное (поле центробежных сил.)
То есть поле потенциально, следовательно A зависит только от начальной и конечной точки, а не от траектории.


Тогда


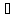
 .
Тогда
.
Тогда

Если

Если


Так
как


 – потенциал
поля относительно бесконечности.
– потенциал
поля относительно бесконечности.
Определим
энергии гравитационного поля
 .
.







 =>
=>

Таким
образом,
 ,
,

Из
формулы из предыдущей лекции получим:

 -
для электрона
-
для электрона
 см
– совпадает
с другим методом вычислений.
см
– совпадает
с другим методом вычислений.
Для
любого материального объекта

Отсюда:
-
Можно оценить гравитационную энергию объекта.
 (не хватает по некоторым рассчетам,
следовательно существует еще какой то
источник энергии в Солнце(даже если
включить сюда энергию термоядерной
реакции)).
(не хватает по некоторым рассчетам,
следовательно существует еще какой то
источник энергии в Солнце(даже если
включить сюда энергию термоядерной
реакции)). -
Если сравнить гравитационный радиус планеты и истинный радиус .
 и
и

Если
 ,
следовательно с планеты нельзя излучать
никакие виды энергии ( в том числе и
свет). То есть, мы эту планету не увидим.
Следовательно, возникает ЧЁРНАЯ
ДЫРА.
,
следовательно с планеты нельзя излучать
никакие виды энергии ( в том числе и
свет). То есть, мы эту планету не увидим.
Следовательно, возникает ЧЁРНАЯ
ДЫРА.





Движение в гравитационном поле


Поставим
задачу о движении двух тел:


Имеем
два тела: массами
 и
и
 .
Одно движется в
.
Одно движется в 

гравитационном поле другого от точки отсчета проведены радиус-векторы.
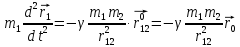 ,
где
,
где
 - единичный вектор.
- единичный вектор.
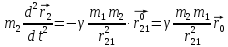
Начальные
условия:
 ,
,
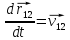 ,
еще наложить условия
,
еще наложить условия

Вычтем:

 – последнее
решать не будем
– последнее
решать не будем
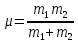
Законы сохранения:

Где
два последних слагаемых есть
 ,
так как L = const по закону сохранения
импульса
,
так как L = const по закону сохранения
импульса
 - функция от r
- функция от r
 часть
часть


Замечания:
-

-
 но
полное не может быть,
но
полное не может быть,


-
 -
для частицы с массой m.
-
для частицы с массой m. -
Единственное решение
 движение
строго по окружности с
движение
строго по окружности с
 .
. -
 ,
то
,
то
 существует два решения в некотором
интервале
существует два решения в некотором
интервале

 движение
по эллипсу.
движение
по эллипсу.
-
 движение
по параболе (разомкнута относительно
движение
по параболе (разомкнута относительно
 ).
). -
 движение
по гиперболе (разомкнута вообще).
движение
по гиперболе (разомкнута вообще).
Космические скорости
-
 .
.
Таким
образом
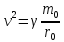
То
есть первая космическая скорость:

Либо
 можно
посчитать:
можно
посчитать:

-
 – у
второй космической параболическая
траектория
– у
второй космической параболическая
траектория -
Если W > 0
 под углом
под углом
 (межпланетные путешествия).
(межпланетные путешествия).
