
- •Розділ 1 твірні функції
- •1.1. Формальні степеневі ряди і твірні функції.
- •Дії над формальними степеневими рядами. Елементарні твірні функції
- •1.1.1. Твірні функції і дії над ними
- •1.1.2. Елементарні твірні функції
- •1 І довільне комплексне число.
- •1.1.3. Диференціювання та інтегрування твірних функцій
- •1.2. Твірні функції для відомих послідовностей
- •1.2.1. Геометрична прогресія
- •1.2.2. Послідовність Фібоначчі.
- •1.2.3. Рекурентні співвідношення і раціональні твірні функції
- •1.2.4. Добуток Адамара раціональних твірних функцій.
- •Розділ 2. Характеристичні функції
- •2.1. Однозначність відповідності
- •2.2. Властивостi характеристичної функцiї
- •2.3. Інші інтегральні перетворення
- •2.4. Генератриси випадкових величин
- •2.5. Формула обертання для характеристичної функцiї
- •2.6. Теорема Левi
- •2.7. Сумiсна характеристична функцiя та слабка збiжнiсть векторiв
- •2.8. Класична центральна гранична теорема
- •Розділ 3
- •3.1. Мета і зміст бжд
- •3.2. Організація навчально-виховного процесу
- •Висновок
2.3. Інші інтегральні перетворення
Одночасно з характеристичними функціями у теорії ймовірностей використовують інші види перетворень.
Означення
2.3.1.
Твірною функцією моментів випадкової
величини
 називається така функція змінної
називається така функція змінної


у
припущенні, що величина під знаком
сподівання інтегрована для всіх
 з деякого околу нуля.
з деякого околу нуля.
Твірна функція моментів розкладається у ряд Тейлора

Логарифмічне
перетворення
 називається твірною функцією кумулят.
Коефіцієнти
називається твірною функцією кумулят.
Коефіцієнти
 розкладу
у ряд Тейлора
розкладу
у ряд Тейлора

називаються
кумулянтами (семіінваріантами) величини
 .
.
Означення
2.3.2 Перетворенням
Лапласа
випадкової
величини
 називається така функція дійсної змінної
називається така функція дійсної змінної


Очевидно,
що для невід'ємних величин
 перетворення Лапласа визначено орректно
та є аналітичною функцією
перетворення Лапласа визначено орректно
та є аналітичною функцією

Зауважимо, що твердження теореми про основні властивості характеристичних функцій, як і інші властивості характеристичних функцій, з необхідними модифікаціями виконуються як для всіх функцій твірних моментів, так і для перетворень Лапласа.
2.4. Генератриси випадкових величин
Для цілочисельних величин використовують метод генератрис, які є дискретними аналогами характеристичних функцій.
Означення
2.4.1.
Нехай
 – невід'ємна цілозначна випадкова
величина з розподілом
– невід'ємна цілозначна випадкова
величина з розподілом
 Генератрисою випадкової величини
Генератрисою випадкової величини
 називається генератриса послідовності
називається генератриса послідовності
 :
:

Остання формула є наслідком теореми про обчислення математичного сподівання функції від дискретної величини.
Теорема 2.4.2 (про властивості генератрис).
а)
ряд
 абсолютно
збігається при
абсолютно
збігається при
 та однозначно визнає розподіл
та однозначно визнає розподіл
 .
.
б)

в)
 при
при
 .
.
г)

д)
якщо величини


е)
) якщо величини
 та
та
 – незалежні в сукупності, а величина
– незалежні в сукупності, а величина
 є сумою випадкового числа
є сумою випадкового числа
 випадкових доданків
випадкових доданків
 вигляду
вигляду

то її генератриса є суперпозицією генератрис

Доведення.
а)
випливає зі збіжності ряду
 ,
однозначність є наслідком формули
обертання
,
однозначність є наслідком формули
обертання

Остання
виводиться з ортогональності гармонік
 у просторі інтегрованих за квадратом
функцій
у просторі інтегрованих за квадратом
функцій
 :
:

б) і в) очевидні.
г)
при
 похідну можна внести під знак суми ряду,
оскільки ряд із похідних збігається
абсолютно
похідну можна внести під знак суми ряду,
оскільки ряд із похідних збігається
абсолютно

Спрямовуючи
тут
 ,
за теоремою Лебега про монотонну
збіжність дістанемо рівність г).
,
за теоремою Лебега про монотонну
збіжність дістанемо рівність г).
д)
випливає з теореми про перетворення
незалежних величин
 ,
та теореми про математичне сподівання
добутку незалежних величин.
,
та теореми про математичне сподівання
добутку незалежних величин.
е) за означенням
 ,
,
де
використано незалежність суми
 і події
і події
 та попередній пункт, внаслідок якого
генератиса суми незалежних у сукупності,
однаково розподілених величин дорівнює
відповідній степені генератриси доданку.
та попередній пункт, внаслідок якого
генератиса суми незалежних у сукупності,
однаково розподілених величин дорівнює
відповідній степені генератриси доданку.
Зауваження.
Твердження
е) залишається справедливим для
дійснозначних величин
 якщо тільки орректно визначено
перетворення
якщо тільки орректно визначено
перетворення
 ,
зокрема для дійсних
,
зокрема для дійсних
 та при
та при
 .
Дійсно, характеристична функція суми
незалежних величин також дорівнює
добуткові характеристичних функцій
доданків.
.
Дійсно, характеристична функція суми
незалежних величин також дорівнює
добуткові характеристичних функцій
доданків.
2.5. Формула обертання для характеристичної функцiї
Теорема 2.5.1 (про формулу обертання для характеристичної функцiї).
Нехай
функцiя
розподiлу
F
має характеристичну функцiю

а)
для
всiх
 ,
що є точками неперервностi
F
справедлива тотожнiсть
,
що є точками неперервностi
F
справедлива тотожнiсть

б)
якщо
функцiя
F
абсолютно
iнтегровна
на
 ,
то
функцiя
розподiлу
F
має щiльнiсть f,
що
дорiвнює
,
то
функцiя
розподiлу
F
має щiльнiсть f,
що
дорiвнює

Зауваження.
Абсолютна збiжнiсть
кратного iнтегралу
в (а) при
 обумовлена обмеженiстю
характеристичної функцiї.
Така збiжнiсть
при
обумовлена обмеженiстю
характеристичної функцiї.
Така збiжнiсть
при
 = 0 може порушуватись.
= 0 може порушуватись.
Доведення.
а)
нехай
випадкова величина
 має функцiю
розподiлу
F,
а величина
має функцiю
розподiлу
F,
а величина
 не залежить вiд
не залежить вiд
 Обчислимо за теоремою Фубiнi
при
Обчислимо за теоремою Фубiнi
при


Нехай
величина
 не залежить вiд
не залежить вiд
 .
Тодi за теоремою про властивостi
характеристичної функцiї, (е), щiльностi
та характеристичнi
.
Тодi за теоремою про властивостi
характеристичної функцiї, (е), щiльностi
та характеристичнi
функцiї
величин
 та
та
 пов’язанi рiвняннями
пов’язанi рiвняннями
 ,
,

Помножимо
попереднє спiввiдношення на
 з
використанням парностi функцiї
з
використанням парностi функцiї
 прийдемо при всiх
прийдемо при всiх
 до тотожностi
до тотожностi

За
теоремою про функцiю
розподiлу
суми незалежних величин лiва
частина збiгається
зi
щiльнiстю
суми незалежних величин
 Тому
Тому

Оскiльки
 ,
i
за нерiвнiстю
Чебишева для дисперсiй
,
i
за нерiвнiстю
Чебишева для дисперсiй
 при
при
 ,
то
,
то
 .
Тому за теоремою про спiввiдношення
слабкої збiжностi
та збiжностi
за ймовiрнiстю
.
Тому за теоремою про спiввiдношення
слабкої збiжностi
та збiжностi
за ймовiрнiстю
 ,
а за теоремою про еквiвалентнiсть
слабкої збiжностi
та в основному
,
а за теоремою про еквiвалентнiсть
слабкої збiжностi
та в основному .
Згiдно
з
означенням збiжностi в основному
.
Згiдно
з
означенням збiжностi в основному

для всiх точок неперервностi функцiї розподiлу F.
б)
за
умови iнтегровностi
знак границi
у формулi
(а) за теоремою Лебега про мажоровану
збiжнiсть
можна внести пiд
знак кратного iнтегралу,
оскiльки
пiдiнтегральний
вираз не перевищує за модулем функцiї
 ,
яка iнтегровна
на
,
яка iнтегровна
на
 за аргументами x,
t.
Пiсля
такого переходу отримуємо
за аргументами x,
t.
Пiсля
такого переходу отримуємо

де
функцiя
f
визначена у формулюваннi
(б). Спрямовуючи тут
 ,
за означенням щiльностi
розподiлу
робимо висновок, що функцiя
розподiлу
F
має щiльнiсть
f
.[3]
,
за означенням щiльностi
розподiлу
робимо висновок, що функцiя
розподiлу
F
має щiльнiсть
f
.[3]
Приклад
2.5.2.
Нехай
 і
і
 – незалежні випадкові величини,
розподілені по нормальному закону з
параметрами
– незалежні випадкові величини,
розподілені по нормальному закону з
параметрами
 і
і
 відповідно. Розглянемо випадкову
величину
відповідно. Розглянемо випадкову
величину
 +
+
 .
Тоді, як було показано в прикладі
2.2.3,
.
Тоді, як було показано в прикладі
2.2.3,
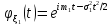 ,
,
 і за властивістю б) характеристичних
функцій отримаємо, шо
і за властивістю б) характеристичних
функцій отримаємо, шо
 .
Але характеристичну функцію
.
Але характеристичну функцію
 смає
випадкова величина, розподілена за
нормальним законом з параметрами
смає
випадкова величина, розподілена за
нормальним законом з параметрами
 .
Тому завдяки взаємно однозначній
відповідності між функцією розподілу
і характеристичною функцією випадкова
величина
.
Тому завдяки взаємно однозначній
відповідності між функцією розподілу
і характеристичною функцією випадкова
величина
 також розподілена нормально ( з параметрами
також розподілена нормально ( з параметрами
 ).
).
Приклад
2.5.3.
Розглянемо незалежні випадкові величини
 і
і
 ,
розподілених по закону Пуассона з
параметрами
,
розподілених по закону Пуассона з
параметрами
 .
Їх характеристичні функції задаються
формулами
.
Їх характеристичні функції задаються
формулами


Нехай
 +
+
 .
Тоді
.
Тоді
 і
знову
-
таки
завдяки
взаємно
однозначній
відповідності
між
функцією
розподілу
і
характеристичною
функцією
випадкова
величина
і
знову
-
таки
завдяки
взаємно
однозначній
відповідності
між
функцією
розподілу
і
характеристичною
функцією
випадкова
величина
 розподілена по закону Пуассона з
параметром
розподілена по закону Пуассона з
параметром
 [4].
[4].
