Вариант 27.
1.
Для указанной
функции
требуется:
а)
найти
естественную
область определения функции:
;
б)
установить
чётность (нечётность) функции:
2.
Даны
комплексные числа
,
и алгебраическое уравнение
.
Требуется:
а)
вычислить
,
,
,
;
б) найти все корни алгебраического уравнения на множестве комплексных чисел.
3. Вычислить пределы (не пользуясь правилом Лопиталя):
а)
б)
в)
г)
4.
Для указанной
функции
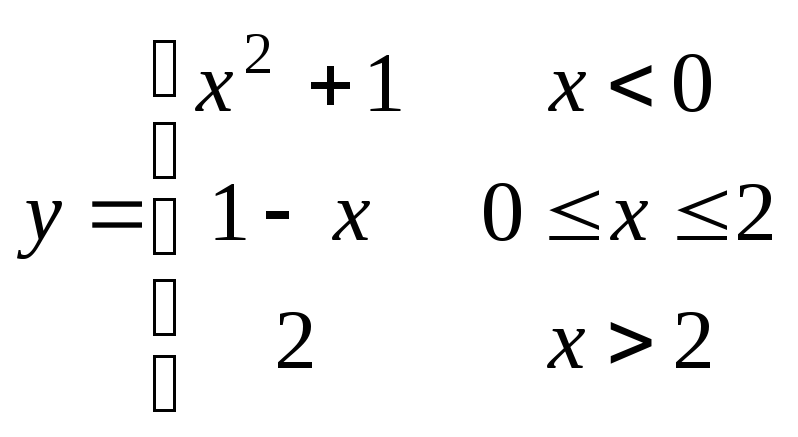требуется
найти точки
разрыва функции и исследовать их
характер.
Построить
график функции.
5.
Найти
производную
:
а)
б)
в)
г)
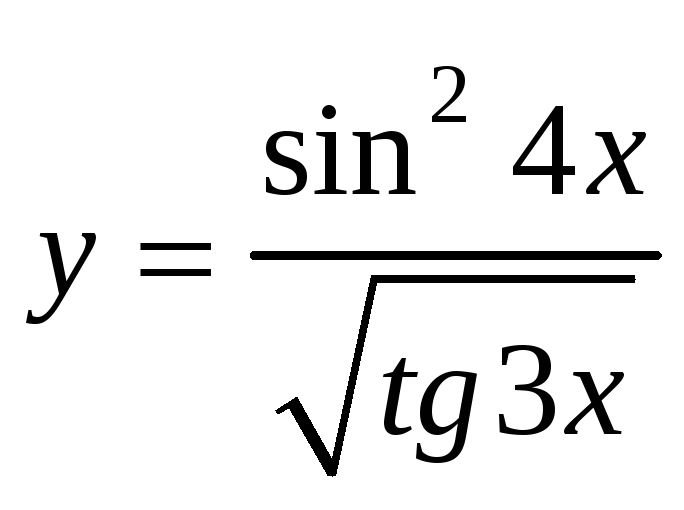д)
6. Вычислить пределы, используя правило Лопиталя.
а)
б)
в)
7.
Для указанной функции
:
,
требуется:
а)
найти
наибольшее и наименьшее значения функции
на отрезке
;
б)
составить уравнение касательной к
графику функции в точке
;
в) провести полное исследование функции и построить её график.
8.
Для указанной
функции
требуется
найти
дифференциал
и
,
если
.
9.
Найти локальные экстремумы функции
10.
Найти градиент
функции
и его величину |
|
в точке
,
если
,
.
Контрольная работа по дисциплине «Математический анализ (часть 1)»
Темы: Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных.
Вариант 28.
1.
Для указанной
функции
требуется:
а)
найти
естественную
область определения функции:
;
б)
установить
чётность (нечётность) функции:
2.
Даны
комплексные числа
,
и алгебраическое уравнение
.
Требуется:
а)
вычислить
,
,
,
;
б) найти все корни алгебраического уравнения на множестве комплексных чисел.
3. Вычислить пределы (не пользуясь правилом Лопиталя):
а)
б)
в)
г)
4.
Для указанной
функции
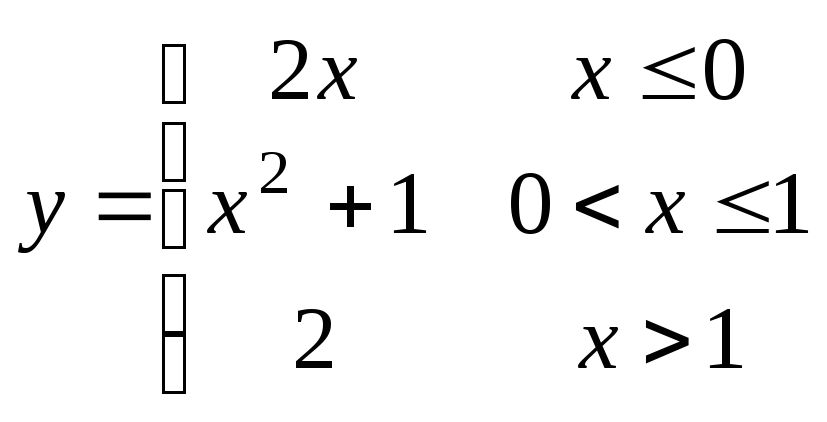требуется
найти точки
разрыва функции и исследовать их
характер.
Построить
график функции.
5.
Найти
производную
:
а)
б)
в)
г)
д)
6. Вычислить пределы, используя правило Лопиталя.
а)
б)
в)
7.
Для указанной функции
:
,
требуется:
а)
найти
наибольшее и наименьшее значения функции
на отрезке
;
б)
составить уравнение касательной к
графику функции в точке
;
в) провести полное исследование функции и построить её график.
8.
Для указанной
функции
требуется
найти
дифференциал
и
,
если
.
9.
Найти локальные экстремумы функции
10.
Найти градиент
функции
и его величину |
|
в точке
,
если
,
.
Контрольная работа по дисциплине «Математический анализ (часть 1)»
Темы: Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных.
Вариант 29.
1.
Для указанной
функции
требуется:
а)
найти
естественную
область определения функции:
;
б)
установить
чётность (нечётность) функции:
2.
Даны
комплексные числа
,
и алгебраическое уравнение
.
Требуется:
а)
вычислить
,
,
,
;
б) найти все корни алгебраического уравнения на множестве комплексных чисел.
3. Вычислить пределы (не пользуясь правилом Лопиталя):
а)
б)
в)
г)
4.
Для указанной
функции
требуется
найти точки
разрыва функции и исследовать их
характер.
Построить
график функции.
5.
Найти
производную
:
а)
б)
в)
г)
д)
6. Вычислить пределы, используя правило Лопиталя.
а)
б)
в)
7.
Для указанной функции
:
,
требуется:
а)
найти
наибольшее и наименьшее значения функции
на отрезке
;
б)
составить уравнение касательной к
графику функции в точке
;
в) провести полное исследование функции и построить её график.
8.
Для указанной
функции
требуется
найти
дифференциал
и
,
если
.
9.
Найти локальные экстремумы функции
10.
Найти градиент
функции
и его величину |
|
в точке
,
если
,
.
Контрольная работа по дисциплине «Математический анализ (часть 1)»
Темы: Введение в анализ. Дифференциальное исчисление функции одной и нескольких переменных.