14

Содержание.

1. Постановка задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3

2. Краткая теория . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4

3. Порядок выполнения работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

4. Алгоритм решения задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7

5. Описание программы расчета . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11

5.1. Описание типов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11

5.2. Описание глобальных переменных . . . . . . . . . . . . . . . . . . . . . . .11

5.3. Описание процедур и функций . . . . . . . . . . . . . . . . . . . . . . . . . . 11

5.4. Тело программы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

Список используемой литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

Приложение. Листинг программы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

1. Постановка задачи.

Исследовать на устойчивость по критерию Михайлова является

ли система автоматизированного регулирования устойчивой, если её работа описана уравнением:

Написать программу, рисующую график кривой Михайлова и делающую выводы об устойчивости данной САР.

2. Краткая теория.

Частотные критерии устойчивости позволяют судить об устойчивости систем автоматического управления по виду их частотных характеристик. Эти критерии являются графоаналитическими и получили широкое распространение, так как позволяют сравнительно легко исследовать устойчивость систем высокого порядка, а также имеют простую геометрическую интерпретацию и наглядность.

Наибольшее распространение среди частотных критериев устойчивости получил критерий Михайлова. Этот критерий устойчивости, сформулированный в 1938г. советским ученым А.В. Михайловым, является, по существу, геометрической интерпретацией принципа аргумента и позволяет судить об устойчивости системы на основании рассмотрения некоторой кривой, называемой кривой Михайлова.

Пусть функционирование - АС описывается линейным дифференциальным уравнением n-го порядка с постоянными вещественными коэффициентами:

. (2.1)

Его характеристическое уравнение имеет вид:

. (2.2)

Критерий устойчивости Михайлова позволяет решить вопрос о расположении корней характеристического уравнения (2.2) на комплексной плоскости и, следовательно, решить вопрос об устойчивости нулевого решения (2.1).

Полагая , получим:

где

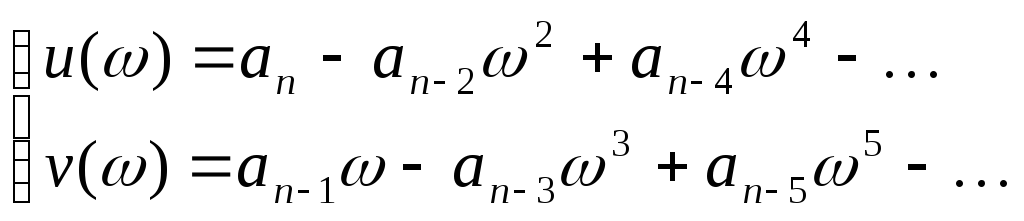(2.3)

Величину при заданном значении параметраможно изобразить в виде вектора на комплексной плоскостис началом в точке 0.

При изменении в интервале, конец этого вектора опишет некоторую кривую, которая называется кривой Михайлова.

Теорема Михайлова. Для асимптотической устойчивости невозмущенного решения уравнения (2.1), характеристическое уравнение которого имеет вид (2.2) и не имеет чисто мнимых корней, необходимо и достаточно, чтобы вектор , описывающий кривую Михайлова, повернулся на угол, гдеn - степень многочлена (2.2).

Практически кривая Михайлова строится следующим образом:

1. Для уравнения n-го порядка составить характеристический многочлен .

2. Составить характеристический комплекс , положив.

3. Найти точки пересечения кривой Михайлова с осями и и , для этого надо решить уравнения и.

4. Для полного представления о поведении исследуемой кривой задать промежуточные значения , по формулам (4.3) вычислитьи, полученные точки соединить плавной кривой.

5. Найти результирующий угол поворота вектора.

6.По формуле определить значение- число корней в кривой положительной полуплоскости и сделать вывод об устойчивости системы.