Содержание:

Задание Введение	2 3	стр. стр.
I. Анализ системы	4	стр.
1.1 Определение ПФ разомкнутой системы и замкнутой в режимах управления, стабилизации и по ошибке	4	стр.
1.2 Составление модели исследуемой системы управления	5	стр.
1.3 Определение показателей качества нескорректированной системы	6	стр.
1.4 ЛАХ, ЛФХ и АФХ для САУ, составленной из функционально необходимых звеньев оценка запасов устойчивости замкнутой САУ	7	стр.
1.5 Вывод	9	стр.
II. Синтез корректирующих устройств (КУ)	10	стр.
2.1 Синтез корректирующих устройств: последовательного и в обратной связи	10	стр.
2.2 Проверка устойчивости скорректированной системы	12	стр.
2.3 Переходная характеристика и определение показателей качества скорректированной системы	14	стр.
2.4 Вывод	15	стр.
III. Теоретические сведения о исследовании нелинейных элементов САУ	16	стр.
Список литературы	22	стр.

Задание

Вариант №24

Исходная структурная схема представлена на рис 1.1.

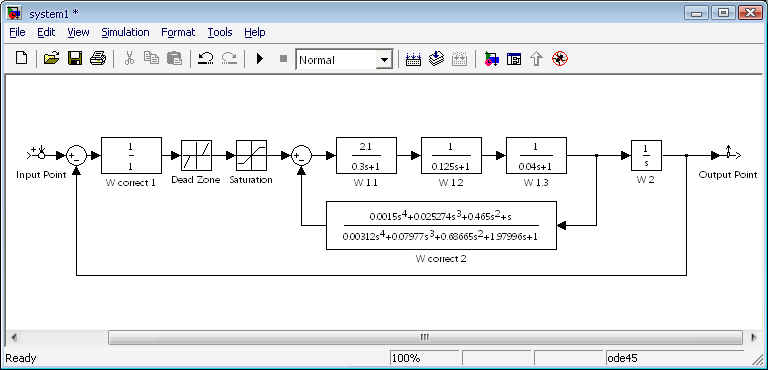
Рис. 1.1 - Исходная структурная схема

Требования к синтезируемой системе
σзад,%	Tзаду, c	c0зад	c1зад	c2зад
30	1,5	0	1/80	1/8

Введение

Принцип действия всякой системы автоматического регулирования (САР) заключается в том, чтобы обнаруживать отклонения регулируемых величин, характеризующих работу объекта или протекание процесса от требуемого режима и при этом воздействовать на объект или процесс так, чтобы устранять эти отклонения. В теории автоматического регулирования основными являются проблемы: устойчивости, качества переходных процессов, статической и динамической точности, автоколебаний, оптимизации, синтеза и отождествления (идентификации). Задачи общей теории автоматического регулирования заключаются в решении перечисленных проблем. При поиске решений используются:

1. Методы анализа устойчивости замкнутых САР.

2. Методы оценки качественных показателей САР.

3. Методы повышения точности САР.

4. Методы коррекции динамических свойств САР.

5. Методы синтеза САР.

Задача коррекции состоит в повышении динамической точности САР в переходных режимах. Она возникает, поскольку стремление снизить ошибки регулирования в типовых режимах, приводит к необходимости использования таких значений общего коэффициента усиления, при которых без принятия специальных мер (внедрения пассивных звеньев) система оказывается неустойчивой.

Синтез системы имеет конечной целью отыскание: 1) рациональной структуры системы и 2) установление оптимальных величин параметров отдельных звеньев. Задача повышения точности САР обычно предполагает существенный пересмотр ее структуры. Возможны замены или добавления отдельных звеньев в контуре.

I. Анализ системы

1. Определение пф разомкнутой системы и замкнутой в режимах управления, стабилизации и по ошибке

На рисунке 1.1 показана схема разомкнутой системы, составленной из функционально необходимых звеньев (без корректирующих устройств).

Рис. 1.2 Схема разомкнутой системы

Передаточной функцией (ПФ) системы автоматического регулирования или какого-либо другого устройства называется отношение преобразования Лапласа выходной величины к преобразованию Лапласа входного сигнала при нулевых начальных условиях.

Передаточная функция разомкнутой системы (f(t)=0):

Передаточная функция разомкнутой системы по возмущению (y(t)=0):

Передаточная функция замкнутой системы без корректирующих устройств:

Передаточная функция замкнутой системы по возмущению (y(t)=0):

Так как у(t)=0

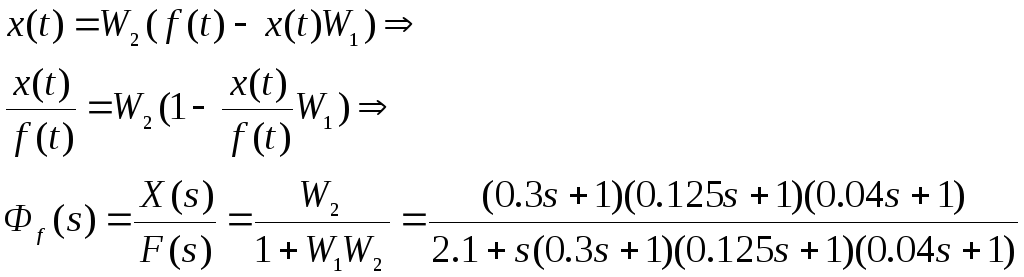
Передаточная функция замкнутой системы относительно ошибки по задающему воздействию (f(t)=0):

Так как f(t)=0

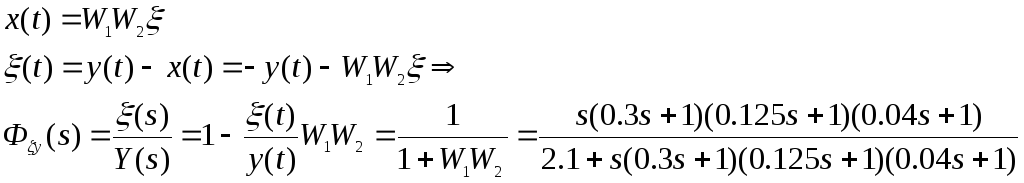
Передаточная функция замкнутой системы относительно ошибки по возмущающему воздействию (y(t)=0):

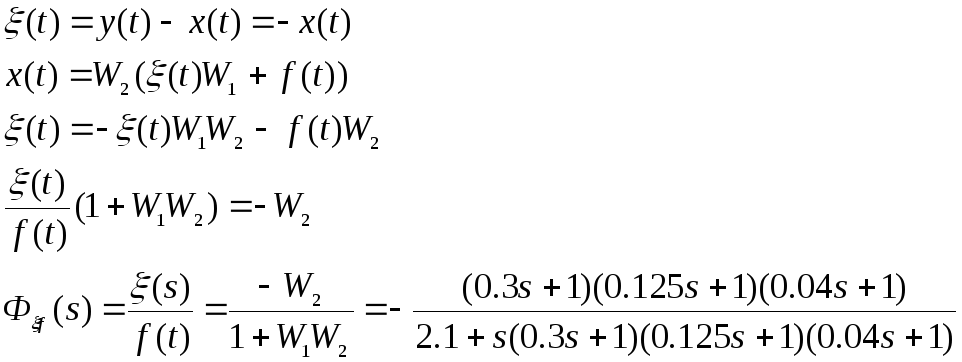
1.2 Составление модели исследуемой системы управления Matlab (Simulink)

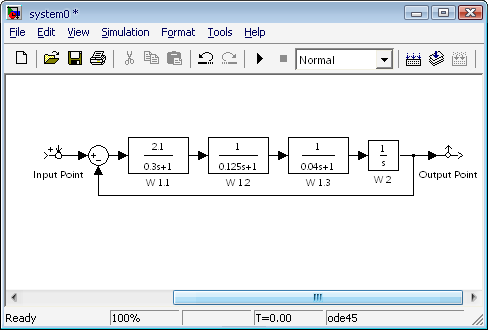
1.2 Определение показателей качества нескорректированной системы

В программном продукте Simulink построим переходную характеристику нескорректированной системы (рис 1.3).

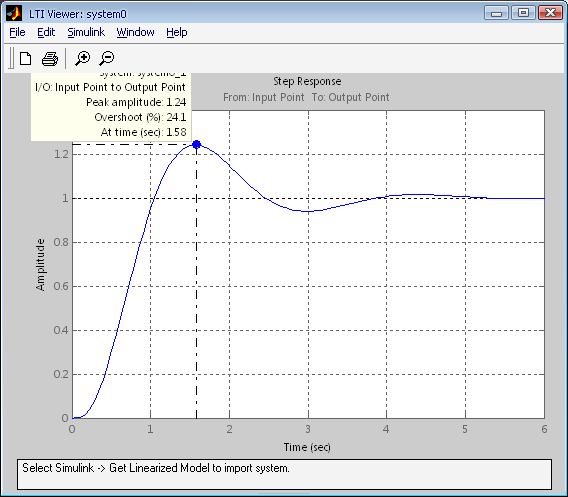
Рис. 1.3 Переходная характеристика

По переходной характеристике определим основные показатели качества:

Время регулирования: Т_у=6 с

Величина перерегулирования:

, где

y_max – максимальное значение амплитуды

y(∞) – величина установившегося значения

1.4 Лах, лфх и афх для сау, составленной из функционально необходимых звеньев оценка запасов устойчивости замкнутой сау

Проверка устойчивости разомкнутой системы по алгебраическому критерию Гурвица.

Передаточная функция разомкнутой системы:

Характеристическое уравнение разомкнутой системы:

,

где

,

,

,

,

.

Все коэффициенты положительны, необходимое условие устойчивости выполняется. Найдем главные миноры матрицы Гурвица:

, ,

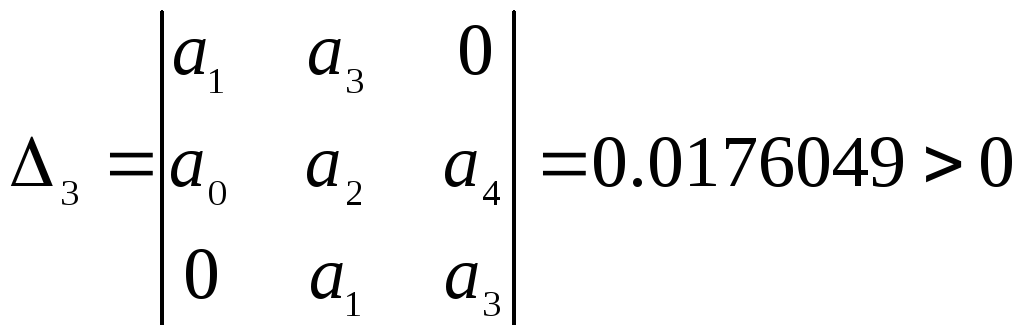Все главные миноры матрицы Гурвица положительны, следовательно, рассматриваемая система является устойчивой по критерию Гурвица.

Используя программное обеспечение Matlab (Simulink), построим ЛАХ и ЛФХ рисунок 1.4:

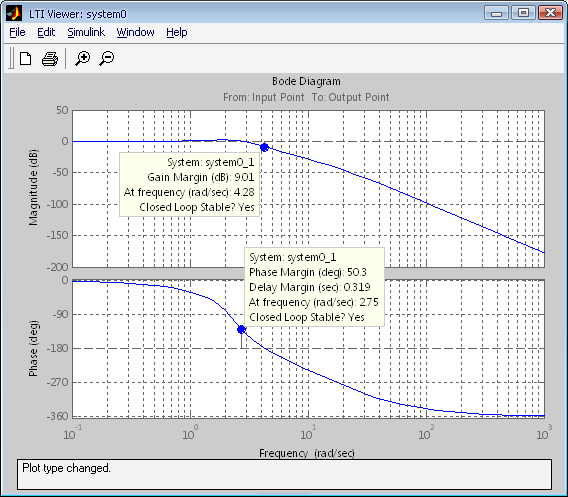
Рис. 1.4 – ЛАХ и ЛФХ САУ, составленной из функционально

необходимых звеньев

Устойчивая в разомкнутом состоянии система будет устойчивой и в замкнутом состоянии, если сдвиг по фазе на частоте среза не достигает -

(-180^°).

Система устойчива.

Запас устойчивости по фазе 50.3º, по амплитуде 9.01 Дб.

Качественно построим амплитудно-фазовую характеристику (АФХ)

рисунок 1.5:

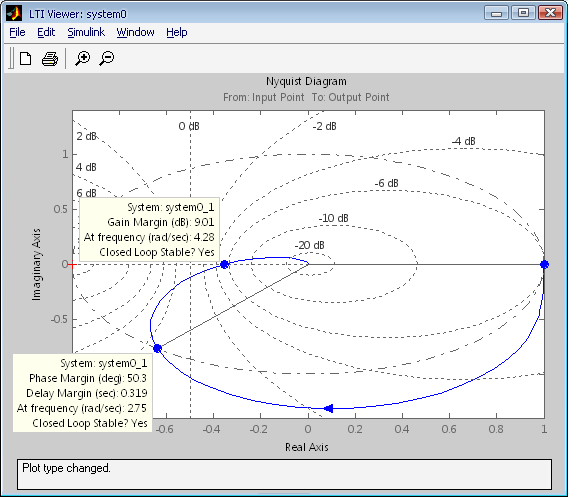
Рис 1.5 – АФХ САУ, без корректирующих устройств

Для проверки устойчивости используем частотный критерий устойчивости Найквиста:

Для устойчивости замкнутой САУ необходимо и достаточно,

чтобы годограф АФХ разомкнутой системы не охватывал точку с координатами (-1, j 0).

В нашем случае годограф не охватывает точку с данными координатами, соответственно, делаем вывод, что система устойчива.