8 Поняття про вектора. Лінійні операції над векторами в координатаній формі.

Вектор - це направлений відрізок Щоб знайти координати вектора потрібно від координат його кінця відняти координати початку (Переміщаючи точки А та В слідкуйте за зміною координат вектора АВ).

При поміщенні початку вектора у початок координат координати вектора будуть рівні координатам його кінця.

Над векторами можна виконати такі лінійні операції:

- множення числа n на вектор. Для множення числа на вектор потрібно помножити це число на кожну з координат вектора, при цьому довжина вектора збільшується у n разів (змінюйте коефіцієнти та координати векторів а та b на рисунку);

- додавання двох векторів. Для додавання векторів потрібно додати відповідні їх координати. Геометрично вектори можна додати за правилом трикутника або паралелограма (перемістіть вектори утворивши відповідно трикутник та паралелограм).

Проекцією вектора на вісь називається взята з відповідним знаком довжина відрізка, що міститься між проекціями початку і кінця даного вектора на цю вісь. Знак плюс береться у тому випадку, якщо від проекції початку до проекції кінця даного вектора на цю вісь необхідно рухатись у напрямку осі Проекцією вектора на вісь називається добуток модуля вектора на косинус кута між напрямком даного вектора і напрямком осі, тобто

9 Розклад вектора за базисом. Лінійні операції над векторами в координатній формі Будь-яку впорядковану сукупність n векторів називають базисом деякого простору, якщо: 1) усі вектори даної сукупності лінійно незалежні; 2) будь-який вектор цього простору є лінійною комбінацією даної сукупності векторів. Сумою двох векторів а=(а1, а2, ....,аn) i b=(b1,b2,....,bn), які належать одному простору і задані звоїми компонентами, називається третій вектор с=(с1, с2,...,сn), компоненти якого дорівнюють сумі відповідних компонент даних векторів: c1=a1+b1; c2=a2+b2; c3=a3+b3,....; cn=an+bn. Різницею двох векторів a i b, які належать одному і тому самому простору, назвемо третій вектор с, компоненти якого дорівнюють різниці компонент векторів a i b: c=a-b=(a1-b1, a2-b2, a3-b3,.....,an-bn)

10 Скалярний добуток векторів, його властивості і обчислення.

Визначення. Скалярним добутком двох векторів називається добуток їх довжин і косинуса кута між ними.

Скалярний добуток двох векторів і позначимо символом . У відповідності з визначенням

Безпосередньо із визначення випливає, що скалярний добуток двох векторів є скаляр.

Кут між двома векторами не залежить від того, який вектор вибирається першим і який другим, тому

тобто скалярний добуток має комутативну властивість.

Оскільки є проекція вектора на вісь, направлену так, як і вектор , є проекція вектора на вісь, направлену по вектору , то

Тепер легко показати, що скалярний добуток векторів має розподільчу властивість, тобто

тоді

Отже .

Неважко перевірити, що скалярний добуток має асоціативну властивість по відношенню до скалярного множника.

_{Із визначення скалярного добутку векторів випливає, що}

_{Отже, скалярний добуток вектора на самого себе дорівнює квадрату довжини вектора. Зокрема}

_{Якщо два вектори взаємно перпендикулярні, то їх скалярний добуток дорівнює нулю. Навпаки, якщо скалярний добуток дорівнює нулю, але ні один із векторів не є нуль, то в нуль повинен обертатися косинус кута між векторами, а тому вектори повинні бути перпендикулярні.}

_{Отже, для того щоб два вектори були перпендикулярні, необхідно і достатньо, щоб їх скалярний добуток дорівнював нулю.}

_{Оскільки напрямок нульового вектора вважається довільним, то можна вважати нульовий вектор перпендикулярним будь-якому вектору. Тому в наведеній умові перпендикулярності двох векторів немає необхідності особливо вказувати, що ні один із векторів не повинен бути нульовим.}

_{Із умови перпендикулярності отримаємо, зокрема, що}

_{Якщо вектори задані своїми координатами в ортонормованому базисі , то, використовуючи розподільчу і сполучну по відношенню до скалярного множника властивості скалярного добутку, одержимо:}

_{тобто скалярний добуток двох векторів дорівнює сумі добутків одноіменних координат цих векторів.}

_{Із визначення скалярного добутку двох векторів безпосередньо знаходиться формула для обчислення косинуса кута між двома векторами}

Кут між векторами

Нехай задано два вектори та .Знайдемо їхній скалярний добуток. Використовуючи властивості 1 і 3 скалярного добутку, дістанемо

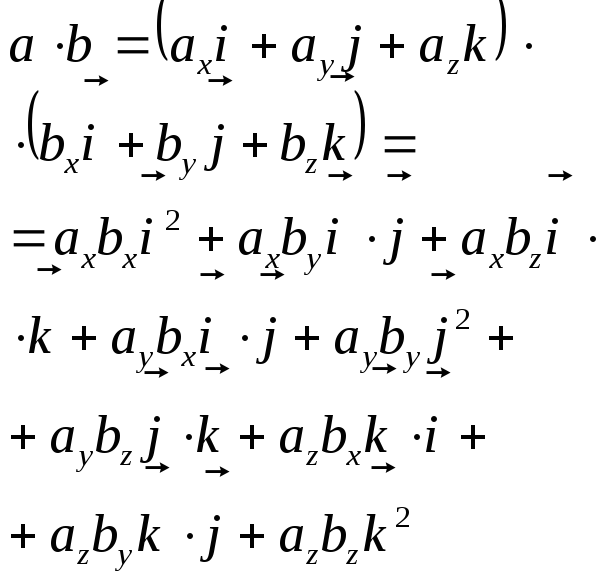
Оскільки - попарно ортогональні орти, то , тому

Отже, скалярний добуток двох векторів, заданих координатами в прямокутній системі координат, дорівнює сумі добутків їхніх відповідних координат.

Вкажемо на ряд важливих висновків

1) Необхідною і достатньою умовою перпендикулярності векторів і є рівність

2) Довжина вектора визначається формулою.

3) Кут між векторами та визначається рівністю

11 Векторний добуток векторів, його властивості, обчислення та застосування.

_{Визначення. Векторним добутком двох векторів називається третій вектор, який має довжину, чисельно рівну площі паралелограма, що побудований назаданих векторах, перпендикулярний площині цих векторів і утворює з впорядкованою парою заданих векторів праву трійку.}

Позначається векторний добуток заданих векторів і символом (іноді позначають .

Оскільки площа паралелограма, побудованого на векторах і , дорівнює добутку довжини цих векторів і синуса кута між ними, то

Вкажемо на основні властивості векторного добутку векторів. Відмітимо передусім, що

_{Дійсно, нехай}

_{Оскільки}

і

Вектори і перпендикулярні одній і тій же площині (площина, визначена векторами і ). Вектори , , утворюють праву трійку. Праву ж трійку утворюють і вектори , , `, тому вектори і мають однакові довжини, перпендикулярні одній і тій же площині і направлені в протилежні сторони. Це означає, що . Отже, при перестановці векторів, що перемножуються, напрямок векторного добутку змінюється на протилежний, а довжина не змінюється.

Можна довести, що векторний добуток двох векторів має сполучну властивість по відношенню до третього – скалярного – співмножника.

_{і має розподільчу властивість:}

_{Із визначення векторного добутку векторів випливає, що векторний добуток колінеарних векторів є завжди нульовий вектор. Зокрема, завжди}

_.

_{Оскільки вектори , , взаємно перпендикулярні, мають одиничні довжини і утворюють праву трійку, то}

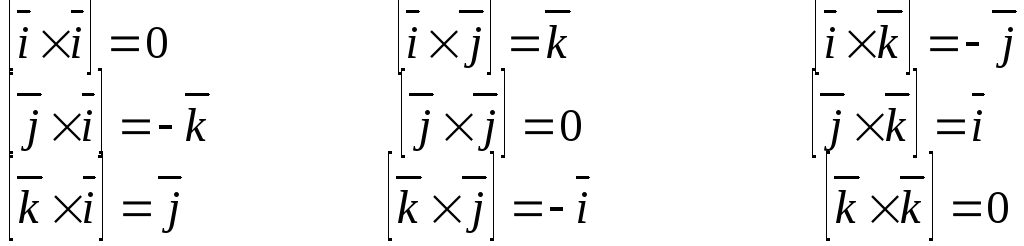
_{Використовуючи розподільчу і сполучну по відношенню до скалярного множника властивості векторного добутку, можна отримати формули для обчислення векторного добутку векторів, заданих шляхом розкладу по ортонормованому базису:}

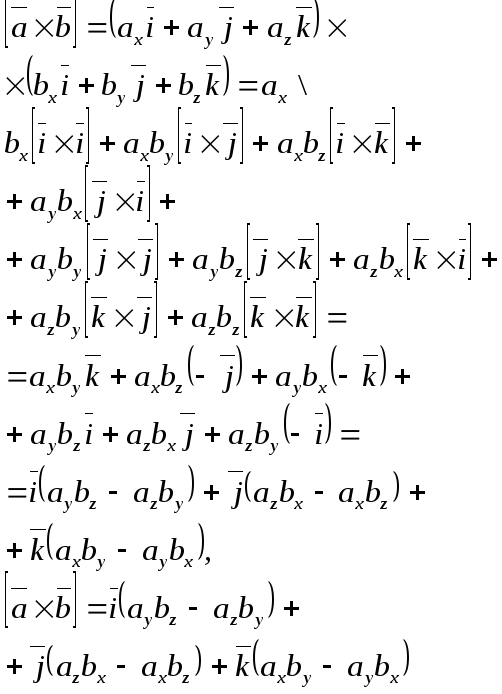
_{Важливою геометричною задачею, яка розв’язується з допомогою введеної операції, є обчислення площини трикутника по координатах його вершин.}

_{Нехай задані координати вершин трикутника А, В, С. Знаючи їх, знаходимо і . Площа трикутника АВС дорівнює половині площі паралелограма, побудованого на векторах і . Отже,}

Приклад. А(1, -2,0); В(2, 1, -1); С(0, 3, 1). Знайти _.

_{Розв’язок}

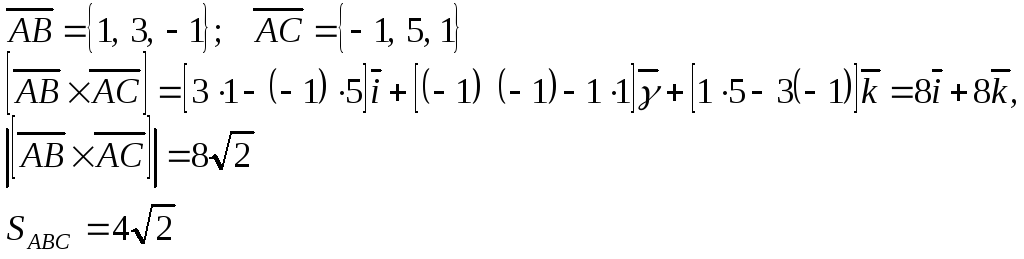
_{Нарешті, формулу для обчислення векторного добутку векторів зручніше записувати через визначник}

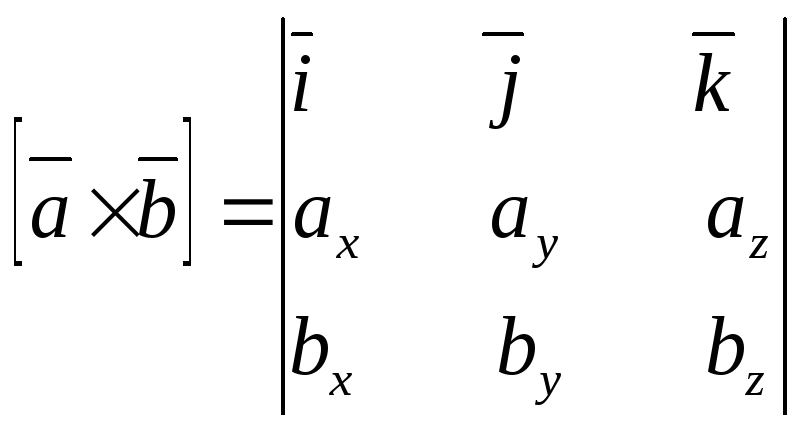_{розкладаючи який по елементах першого рядка, отримаємо формулу}