6 Правило Крамера розв’язування системи лінійних рівнянь
Метод Крамера (Крамера правило) — спосіб розв'язання квадратних систем лінійних алгебраїчних рівнянь із ненульовим визначником основної матриці (при цьому для таких рівнянь розв'язок існує і є єдиним).
Опис методу
Для системи n лінійних рівнянь з n невідомими (над довільним полем)
з визначником матриці системи Δ, що не рівний нулеві, розв'язок записується у такому вигляді:
(i-й стовпчик матриці системи замінюється стовпчиком вільних членів).
Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c1, c2, …, cn виконується рівність:
У такій формі формула Крамера справедлива без припущення, що Δ не рівне нулю, не треба навіть, аби коефіцієнти системи були елементами цілісного кільця (визначник системи навіть може бути дільником нуля у кільці коефіцієнтів). Також можна вважати, що або набори b1,b2,...,bn та x1,x2,...,xn, або набір c1,c2,...,cn складаються не з елементів кільця коефіциєнтів системи, а деякого модуля над цим кільцем.
7 Метод Гауса розв’язування систем лінійних рівнянь
Він оснований на приведенні матриці системи до трикутного вигляду. Це досягається послідовним виключенням невідомих з рівнянь системи. Спочатку за допомогою першого рівняння вик лючається зі всіх наступних рівнянь системи. Потім за допомогою другого рівняння виключається з третього і всіх наступних рівнянь. Цей процес, який називається прямим ходом метода Гаусса, продовжується до тих пір, поки в лівій частині останнього ( -го) рівняння не залишиться лише член з невідомим , тобто матриця системи не буде приведена до трикутного вигляду. (Відмітимо, що к такому вигляду приводиться лише невироджена матриця. В іншому випадку метод Гаусса застосовувати не можна.)
Зворотній хід метода Гаусса полягає у послідовному обчисленні шуканих невідомих: розв’язуючи останнє рівняння, знаходимо єдине невідоме . Далі, використовуючи це значення, з попереднього рівняння обчислюємо і т. д. Останнім знайдемо з першого рівняння.
Розглянемо застосування метода Гаусса для системи
Для виключення з другого рівняння додамо до нього перше, помножене на
-a21/a11. Потім, помноживши перше рівняння на –a31/a11 і додавши результат до третього рівняння, також x1 виключимо з нього . Отримаємо рівнозначну систему рівнянь вигляду
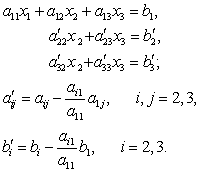
Тепер з третього рівняння системи треба виключити x2 . Для цього помножимо друге рівняння на
-a'32/a'22 і додамо результат до третього. Отримаємо:
Матриця системи має трикутний вигляд. На цьому закінчується прямий хід метода Гаусса.
Відмітимо, що в процесі виключення невідомих доводиться виконувати операції ділення на коефіцієнти , , і т. д. Тому вони мають бути відмінними від нуля; в іншому випадку необхідно відповідним чином переставити рівняння системи.
Зворотній хід починається з розв’язання третього рівняння системи x3=b''3/a''33
Використовуючи це значення, можна знайти з другого рівняння, а потім з першого:
