Анализ статистической значимости параметров модели парной регрессии

Значения , соответствующие данным при теоретических значениях и являются случайными. Случайными являются и рассчитанные по ним значения коэффициентов и .

Надежность получаемых оценок и зависит от дисперсии случайных отклонений (ошибок). По данным выборки эти отклонения и, соответственно, их дисперсия не оцениваются – в расчетах используются отклонения зависимой переменной от ее расчетных значений : . Так как ошибки (остатки) нормально распределены, то среднеквадратическое отклонение ошибок используется для измерения этой вариации. Среднеквадратические отклонения коэффициентов известны как стандартные ошибки (отклонения):

(3.17)

где - среднее значение независимой переменной х;

стандартная ошибка, вычисляемая по формуле (3.16);

.

Проверка значимости отдельных коэффициентов регрессии связана с определением расчетных значений t-критерия (t–статистики) для соответствующих коэффициентов регрессии:

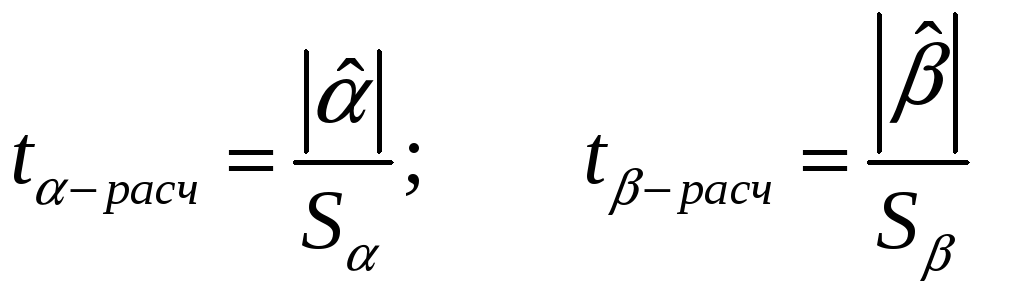(3.18)

Затем расчетные значения сравниваются с табличными t_табл. Табличное значение критерия определяется при (n-2) степенях свободы (n - число наблюдений) и соответствующем уровне значимости  (0,1; 0,05)

Если расчетное значение t-критерия с (n - 2) степенями сво­боды превосходит его табличное значение при заданном уровне зна­чимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует ис­ключить из модели (при этом ее качество не ухудшится).

Интервальная оценка параметров модели

Для значимого уравнения регрессии представляет интерес построение интервальных оценок для параметра :

(3.19)

свободного члена :

где t_табл определяется по таблице распределения Стьюдента для уровня значимости  и числа степеней свободы k = n - 2;

, – стандартные отклонения, соответственно, свободного члена и коэффициента модели (3.6);

n – число наблюдений.

Прогнозирование с применением уравнения регрессии

Регрессионные модели могут быть использованы для прогнозирования возможных ожидаемых значений зависимой переменной.

Прогнозируемое значение переменной получается при подстановке в уравнение регрессии

(3.20)

ожидаемой величины фактора . Данный прогноз называется точечным. Значение независимой переменной не должно значительно отличаться от входящих в исследуемую выборку, по которой вычислено уравнение регрессии.

Вероятность реализации точечного прогноза теоретически равна нулю. Поэтому рассчитывается средняя ошибка прогноза или доверительный интервал прогноза с достаточно большой надежностью.

доверительные интервалы, зависят от стандартной ошибки (3.16), удаления от своего среднего значения , количества наблюдений n и уровня значимости прогноза α. В частности, для прогноза (3.20) будущие значения с вероятностью (1 - α) попадут в интервал

.

Пример 3.3

Используя данные примера 3.1, оценить накопления семьи, имеющей доход 42 тыс. $ и отобразить на графике исходные данные, результаты моделирования и прогнозирования.

Решение

В примере 3.1 была построена модель зависимости накопления от дохода:

.

Для того, чтобы определить накопления семьи при доходе 42 тыс.$ необходимо подставить значение х_прогн в полученную модель.

y_{прогноз} = - 2.184+0.143*42= 3.827

Величину отклонения от линии регрессии вычисляют по формуле , используя данные таблицы 3.4. Величину находят по формуле (3.16):

= = 0.9112

Табл. 3.4.

Наблюдение	Накопления	Предсказанное Y	Остатки	2
	Y		
1	3	3.541	-0.5406	0.2923
2	6	5.688	0.3125	0.0977
3	5	4.256	0.7438	0.5532
4	3.5	2.109	1.3906	1.9338
5	1.5	2.109	-0.6094	0.3713
6	4.5	4.972	-0.4719	0.2227
7	2	2.825	-0.8250	0.6806
Сумма	25.5	25.500	0.0000	4.1516

Коэффициент Стьюдента для m=5 степеней свободы (m=n-2) и уровня значимости 0.1 равен 2.015. Тогда

U_{(x=42,n=7,=0.1)} ==

===1.965

Таким образом, прогнозное значение =3.827 будет находиться между верхней границей, равной 3.827+1.965=5.792 и нижней границей, равной 3.827-1.965=1.862.

График исходных данных и результаты моделирования приведены на рисунке 3.5

Рисунок 3.5. График модели парной регрессии зависимости накопления от дохода.

Нелинейная регрессия

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Теоретические вопросы, связанные с построением моделей нелинейной регрессии следует изучить по учебнику «Эконометрика» под ред. И.И. Елисеевой стр.62-80.

Пример 3.4.

По семи предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений ( Х, млн. руб. ).

Y	64	56	52	48	50	46	38
X	64	68	82	76	84	96	100

Требуется:

1.Для характеристики Y от Х построить следующие модели:

• линейную (для сравнения с нелинейными),

• степенную,

• показательную,

• гиперболическую.

2.Оценить каждую модель, определив:

• индекс корреляции,

• среднюю относительную ошибку,

• коэффициент детерминации,

• F-критерий Фишера.

3.Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.

4.Рассчитать прогнозные значения результативного признака по лучшей модели, если объем капиталовложений составит 89,573 млн. руб.

5.Результаты расчетов отобразить на графике.