
методические указания по курсовой работе / TAY казань
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н. ТУПОЛЕВА
КАФЕДРА ТЕОРЕТИЧЕСКОЙ РАДИОТЕХНИКИ И ЭЛЕКТРОНИКИ
Базлов Е.Ф., Козлов В.А.
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ
ПРЕОБРАЗОВАНИЕ СИГНАЛА В ЦИФРОВОМ ФИЛЬТРЕ.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КУРСОВОЙ РАБОТЕ
Казань 2005г.

ЗАДАНИЕ.
1.Определить спектральную плотность X(ω) непериодического сигнала x(t).
Рассчитать и построить график модуля его спектральной плотности.
2. Найти верхнюю частоту в спектре сигнала, для чего выполнить следующее. Задать погрешность аппроксимации сигнала. Для сигналов, изменяющихся плавно и сравнительно медленно (рис. 1, 2, 5, 7), погрешность задать равной 0,01, а для тех, которые изменяются быстро, скачками (рис. 3, 4, 6, 8, 9, 10) погрешность должна быть равна 0,1. Выбрать произвольно ωmax, а затем вычислить обратное преобразование Фурье в пределах (-ωmax, ωmax), где ωmax=2πfmax. Таким образом, будет произведена аппроксимация сигнала x(t) сигналом xv(t) со спектром, ограниченным частотным диапазоном (-ωmax, ωmax).
Сравнить этот восстановленный сигнал xv(t) c исходным сигналом x(t), для чего вычислить среднеквадратическую погрешность аппроксимации . Погрешность рекомендуется вычислить на временном интервале, соответствующем длительности сигнала. Если будет больше заданной, увеличить ωmax и повторить вычисления. Эту процедуру повторять до тех пор, пока не уменьшится до заданной.
Для найденного значения ωmax, вычислить интервал дискретизации T в соответствии с теоремой Котельникова, а затем определить число отсчетов, соответствующее этому T. Если N окажется дробным, округлить его до целого, обозначив его через N1. После этого уточнить интервал дискретизации, обозначив его через T1, а затем найти значение ωmax, соответствующее T1. Построить дискретизированный сигнал.
3.Записать выражение ДПФ полученного дискретизированного сигнала и вычислить его. Построить график модуля ДПФ. Сделать выводы о характере спектра дискретизированного сигнала.
4.Сравнить модуль ДПФ для n=5 и 10 с модулем спектральной плотности
X(ω) на частотах, соответствующих этим значениям n. Сделать выводы о со-
ответствии ДПФ и спектральной плотности X(ω).
5. По заданному на z-плоскости расположению нулей и полюсов системной функции цифрового фильтра записать выражение системной функцииH(z) и нарисовать структурную схему фильтра.
6.Вывести формулу импульсной характеристики g(nT) фильтра, рассчитать
ееи построить график g(nT).
7.Вывести формулу частотной характеристики фильтра, рассчитать и построить график его амплитудно-частотной характеристики.
8.Записать разностное уравнение цифрового фильтра и вычислить выходной сигнал, построить его. Сделать выводы об искажениях сигнала при прохождении его через фильтр.
9.Записать выражение ДПФ сигнала на выходе фильтра и вычислить его. Построить график ДПФ выходного сигнала.
2

|
|
|
ВАРИАНТЫ ЗАДАНИЙ. |
|
||
Характеристики входного сигнала |
Нули и полюсы системной функции |
|||||
|
|
|
|
|
|
|
№ |
x(t) |
τ1 |
τ2 |
α |
Нули |
Полюсы |
вар |
рис. |
с |
с |
с-1 |
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
1 |
10-4 |
- |
- |
z01=0, z02,3=±j0.5 |
z*1=0.8, |
|
|
|
|
|
|
z*2,3=0.6exp(±jπ/3) |
2 |
2 |
10-4 |
- |
- |
z01=0, z02,3=±j0.3 |
z*1=0.5, |
|
|
|
|
|
|
z*2,3=0.7±j0.5 |
3 |
3 |
10-4 |
- |
- |
z01=0, z02,3=±j0.9 |
z*1=0.8, |
|
|
|
|
|
|
z*2,3=0.5exp(±jπ/4) |
4 |
4 |
10-4 |
- |
- |
z01=0, z02,3=j0.75 |
z*1=0.9, |
|
|
|
|
|
|
z*2,3=0.5exp(±jπ/6) |
|
|
-4 |
|
- |
|
z*1=0.7, |
5 |
5 |
10 |
- |
|
z01=0, z02,3=±j0.25 |
z*2,3=0.5exp(±jπ/2) |
6 |
6 |
10-4 |
4 10-4 |
- |
z01=0.1, |
z*1=0.8, |
|
|
|
|
|
z02,3=±j0.25 |
z*2б3=0.6exp(±jπ/3) |
7 |
7 |
- |
- |
103 |
z01=0.1, z02=0.3, |
z*1=0.8, |
|
|
|
|
|
z03=0.7 |
z*2,3=0.6exp(±jπ/3) |
8 |
8 |
10-4 |
2 10-4 |
- |
z01=-0.5, |
z*1=0.5, |
|
|
|
|
|
z02,3=±0.85 |
z*2,3=0.7±j0.5 |
9 |
9 |
10-4 |
- |
- |
z01=-0.75, |
z*1=0.9, |
|
|
|
|
|
z02,3=±0.35 |
z*2,3=0.5exp(±jπ/6) |
10 |
10 |
10-4 |
2 10-4 |
- |
z01=-0.75, |
z*1=0.5, z*2,3= |
|
|
|
|
|
z02,3=±0.35 |
-0.8exp(±jπ/3) |
11 |
1 |
2 10-4 |
- |
- |
z01=0.5, |
z*1=0, |
|
|
|
|
|
z02,3=0.7±j0.5 |
z*2,3=±j0.3 |
12 |
2 |
2 10-4 |
- |
- |
z01=0.8, |
z*1=0, |
|
|
|
|
|
z02,3=0.5exp(±jπ/4) |
z*2,3=±j0.9 |
13 |
3 |
2 10-4 |
- |
- |
z01=0.9, |
z*1=0, |
|
|
|
|
|
z02,3=0.5exp(±jπ/6) |
z*2,3=±j0.75 |
14 |
4 |
2 10-4 |
- |
- |
z01=0.7, |
z*1=0, |
|
|
|
|
|
z02,3=0.5exp(±jπ/2) |
z*2,3=±j0.25 |
15 |
5 |
2 10-4 |
- |
- |
z01=0.7, |
z*1=0, |
|
|
|
|
|
z02,3=0.5exp(±jπ/2) |
z*2,3=±j0.25 |
16 |
6 |
2 10-4 |
5 10-4 |
- |
z01=0.8, |
z*1=0.1, |
|
|
|
|
|
z02,3=0.6exp(±jπ/3) |
z*2,3=±j0.25 |
17 |
7 |
- |
- |
2 103 |
z01=0.8, |
z*1=0.1, z*2=0.3 |
|
|
|
|
|
z02,3=0.9exp(±jπ/4) |
z*3=0.7 |
18 |
8 |
2 10-4 |
3 10-4 |
- |
z01=0.5, |
z*1=-0.5, |
|
|
|
|
|
z02,3=0.7±j0.5 |
z*2,3=±j0.85 |
3
1 |
2 |
3 |
4 |
5 |
19 |
9 |
2 10-4 |
- |
- |
|
|
|
|
|
20 |
10 |
2 10-4 |
3 10-4 |
- |
|
|
|
|
|
21 |
1 |
4 10-4 |
- |
- |
|
|
|
|
|
22 |
2 |
4 10-4 |
- |
- |
|
|
|
|
|
23 |
3 |
4 10-4 |
- |
|
|
|
|
|
|
24 |
4 |
4 10-4 |
- |
- |
|
|
|
|
|
25 |
5 |
4 10-4 |
- |
|
|
|
|
|
|
26 |
6 |
4 10-4 |
9 10-4 |
- |
|
|
|
|
|
27 |
7 |
- |
- |
500 |
|
|
|
|
|
28 |
8 |
4 10-4 |
5 10-4 |
- |
|
|
|
|
|
29 |
9 |
4 10-4 |
- |
- |
|
|
|
|
|
30 |
10 |
4 10-4 |
5 10-4 |
- |
|
|
|
|
|
31 |
1 |
5 10-4 |
- |
- |
|
|
|
|
|
32 |
2 |
5 10-4 |
- |
- |
|
|
|
|
|
33 |
3 |
5 10-4 |
- |
- |
|
|
|
|
|
34 |
4 |
5 10-4 |
- |
- |
|
|
|
|
|
35 |
5 |
5 10-4 |
- |
- |
|
|
|
|
|
36 |
6 |
5 10-4 |
2 10-3 |
- |
|
|
|
|
|
37 |
7 |
- |
- |
250 |
|
|
|
|
|
38 |
8 |
5 10-4 |
5 10-3 |
- |
|
|
|
|
|
39 |
9 |
5 10-4 |
- |
- |
|
|
|
|
|
6
z01=0.9, z02,3=0.5exp(±jπ/6) z01=0.5 z02,3=- 0.8exp(±jπ/3)
z01=0.5 z02,3=- 0.8exp(±jπ/3)
z01=0.9, z02,3=0.5exp(±jπ/6) z01=0.5, z02,3=0.7±j0.5 z01=0.8, z02,3=0.9exp(±jπ/4) z01=0.8, z02,3=0.6exp(±jπ/3) z01=0.9, z02,3=0.5exp(±jπ/6) z01=0.8, z02,3=0.5exp(±jπ/4) z01=0.5, z02,3=0.7±j0.5 z01=0.8, z02,3=0.6exp(±jπ/3) z01=-0.75, z02,3=±0.35 z01=-0.75, z02,3=±0.35 z01=-0.5, z02,3=±0.85
z01=0.1, z02=0.3, z03=0.7
z01=0.1, z02,3=±j0.25
z01=0, z02,3=±j0.25
z01=0, z02,3=j0.75
z01=0, z02,3=±j0.9
z01=0, z02,3=±j0.3
z01=0, z02,3=±j0.5
7
z*1=-0.75, z*2,3=±j0.35
z*1=-0.75, z*2,3=±j0.35
z*1=-0.75, z*2,3=±j0.35
z*1=-0.75, z*2,3=±j0.35
z*1=-0.5, z*2,3=±0.35
z*1=0.1, z*2=0.3 z*3=0.7
z*1=0.1, z*2,3=±j0.25
z*1=0, z*2,3=±j0.75
z*1=0, z*2,3=±j0.9
z*1=0, z*2,3=±j0.3
z*1=-0, z*2,3=±j0.5
z*1=0.5, z*2,3= -0.8exp(±jπ/3)
z*1=0.9, z*2,3=0.5exp(±jπ/6)
z*1=0.5, z*2,3=0.7±j0.5
z*1=0.8, z*2,3=0.9exp(±jπ/4)
z*1=0.8, z*2,3=0.6exp(±jπ/3)
z*1=0.7, z*2,3=0.5exp(±jπ/2)
z*1=0.9, z*2,3=0.5exp(±jπ/6)
z*1=0.8, z*2,3=0.5exp(±jπ/4)
z*1=0.5, z*2,3=0.7±j0.5
z*1=0.8, z*2,3=0.6exp(±jπ/3)
4
1 |
2 |
3 |
4 |
5 |
40 |
10 |
5 10-4 |
5 10-3 |
- |
|
|
|
|
|
41 |
1 |
10-5 |
- |
- |
|
|
|
|
|
42 |
2 |
10-5 |
- |
- |
43 |
3 |
10-5 |
- |
- |
|
|
|
|
|
44 |
4 |
10-5 |
- |
- |
45 |
5 |
10-5 |
- |
- |
|
|
|
|
|
46 |
6 |
10-5 |
3 10-5 |
- |
47 |
7 |
- |
- |
104 |
|
|
|
|
|
48 |
8 |
10-5 |
5 10-5 |
- |
49 |
9 |
10-5 |
- |
- |
|
|
|
|
|
50 |
10 |
10-5 |
5 10-5 |
- |
51 |
1 |
2 10-5 |
- |
- |
|
|
|
|
|
52 |
2 |
2 10-5 |
- |
- |
|
|
|
|
|
53 |
3 |
2 10-5 |
- |
- |
|
|
|
|
|
54 |
4 |
2 10-5 |
- |
- |
|
|
|
|
|
55 |
5 |
2 10-5 |
- |
- |
|
|
|
|
|
56 |
6 |
2 10-5 |
5 10-5 |
- |
|
|
|
|
|
57 |
7 |
- |
- |
2 104 |
|
|
|
|
|
58 |
8 |
2 10-5 |
2 10-4 |
- |
|
|
|
|
|
59 |
9 |
2 10-5 |
- |
- |
|
|
|
|
|
60 |
10 |
2 10-5 |
2 10-4 |
- |
|
|
|
|
|
6
z01=0, z02,3=±j0.3
z01=0, z02,3=j0.75
z01=0.1, z02=-j0.25, z03=j0.25
z01=-0.5, z02,3=±0.85 z01=-0.75, z02,3=±0.35 z01=0.5, z02,3=0.7±j0.5 z01=0.9, z02,3=0.5exp(±jπ/6) z01=0.8, z02,3=0.6exp(±jπ/3) z01=0.5, z02,3=0.7±j0.5 z01=0.5 z02,3=- 0.8exp(±jπ/3)
z01=0.5 z02,3=- 0.8exp(±jπ/3)
z01=0.5, z02,3=0.7±j0.5 z01=0.8, z02,3=0.6exp(±jπ/3) z01=0.9, z02,3=0.5exp(±jπ/6) z01=0.5, z02,3=0.7±j0.5 z01=-0.75, z02,3=±0.35 z01=-0.5, z02,3=±0.85 z01=0.1, z02,3=±j0.25
z01=0, z02,3=j0.75
z01=0, z02,3=±j0.3
z01=0, z02,3=±j0.5
7
z*1=0.5, z*2,3=0.7±j0.5
z*1=0.9, z*2,3=0.5exp(±jπ/6)
z*1=0.8, z*2,3=0.6exp(±jπ/3)
z*1=0.5, z*2,3=0.7±j0.5
z*1=0.5, z*2,3= -0.8exp(±jπ/3)
z*1=0, z*2,3=±j0.3
z*1=0, z*2,3=±j0.75
z*1=0.1, z*2,3=±j0.25
z*1=-0.5, z*2,3=±j0.85
z*1=-0.75, z*2,3=±j0.35
z*1=-0.75, z*2,3=±j0.35
z*1=-0.5, z*2,3=±j0.85
z*1=0.1, z*2,3=±j0.25
z*1=0, z*2,3=±j0.75
z*1=0, z*2,3=±j0.3
z*1=0.5, z*2,3= -0.8exp(±jπ/3)
z*1=0.5, z*2,3=0.7±j0.5
z*1=0.8, z*2б3=0.6exp(±jπ/3)
z*1=0.9, z*2,3=0.5exp(±jπ/6)
z*1=0.5, z*2,3=0.7±j0.5
z*1=0.8, z*2,3=0.6exp(±jπ/3)
5
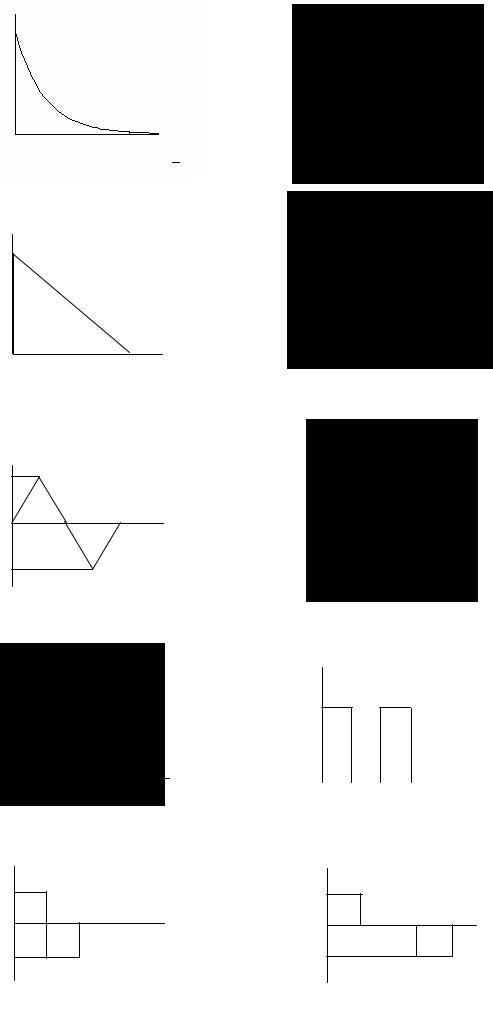
x(t) E
τ1 t
Рис.1
x(t) E
τ1 t
Рис.3
x(t) E
τ1 |
2τ1 t |
-E
Рис.5
x(t) E
exp(-αt) τ1=4.6/α
t
Рис.7
x(t) E
τ1 2τ1 |
t |
-E
Рис.9
x(t) E
τ1 |
2τ1 t |
Рис.2 |
|
x(t) E
τ1 t
Рис.4
x(t) E
τ1 |
τ2-τ1 τ2 t |
Рис.6
x(t)
E
|
t |
τ1 τ2 τ1+τ2 |
Рис.8
x(t)
E
τ2 τ1+τ2 τ1 t
-E
Рис.10
6

МЕТОДИЧЕСКИЕ УКАЗАНИЯ
1. Дискретное преобразование Фурье.
Дискретное преобразование Фурье
|
N−1 |
|
2π |
|
|
|
|
−jnk N |
, n=0,1,2……N-1 |
(1) |
|||
|
||||||
X(nΩ) = T ∑x(kT)e |
|
|
||||
k=0
дает возможность рассчитать дискретный спектрX(nΩ) по отсчетам дискре-
тизированного сигнала x(t). Спектр вычисляется на частотах nΩ=n2π/Tc, где Tc
– длительность сигнала, N= Tc/T+1 – общее число выборок в спектре, T – интервал дискретизации, который задается исходя из теоремы Котельникова. Расстояние между частотными выборками определяется длительностью сигнала Tc=NT. Изменение интервала дискретизации T при заданной длительности сигнала приводит к изменению числа выборок N и, следовательно, к изменению верхней частоты, до которой ведется расчет.
ДПФ является комплексной функцией, поэтому для (1) можно записать:
|
= T |
N−1 |
|
|
|
|
|
|
2π |
− jT |
N−1 |
2π |
=A(nΩ) − jB(nΩ) = |
|
||
X(nΩ) |
∑ x(kT) cos nk |
|
N |
∑ x(kT) sin nk |
N |
|
||||||||||
|
|
k=0 |
|
|
|
|
|
|
|
|
|
k=0 |
|
(2) |
||
|
|
|
|
|
|
|
|
|
B(nΩ) |
|
|
|
||||
|
|
|
|
|
−arctg |
. |
|
|
|
|
||||||
= A 2 |
(nΩ) + B2 |
|
|
|
|
|
||||||||||
(nΩ)e |
|
|
|
|
A(nΩ) |
|
|
|
|
|||||||
|
|
A |
2 |
(nΩ) + B |
2 |
(nΩ) – |
амплитудно-частотная характеристика |
|||||||||
X(nΩ) = |
|
|
||||||||||||||
спектра; |
|
|
|
|
B(nΩ) |
|
|
|
|
|
|
|
|
|
|
|
ψ(nΩ) = −arctg |
– фазо-частотная характеристика. |
|
||||||||||||||
A(nΩ) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ДПФ является периодической функцией частоты с периодом, равным NΩ=2π/T. Таким образом, спектр X(nΩ) на интервале 0≤n≤N-1 равен спектру
сигнала x(kT), причем первые N/2-1 линий соответствуют спектральным линиям x(kT) на положительных частотах, а последние N/2-1 линий ДПФ соответствуют спектральным линиям на отрицательных частотах.
Так как производится анализ детерминированного сигнала, можно получить выражение ДПФ в замкнутой форме. Для этого можно воспользоваться известной суммой:
N∑−1bk e−j2π |
nk |
1 − b N |
|
|
||||
N |
= |
|
|
. |
||||
|
|
−j2π |
n |
|
||||
k=0 |
|
|
|
|||||
− be |
N |
|
|
|||||
1 |
|
|
|
|||||
7
2. Определение z-преобразования функции дискретного времени.
Математическое описание процесса цифровой обработки сигналов основано на представлении их в виде функции дискретного времени или, что то же, чи-
словых последовательностей: |
|
x(0), x(1), x(2), x(3),…….x(k)…… |
(3) |
Целочисленные индексы i=0, 1, 2, 3, ….к…. имеют смысл текущего времени. Если указать значение периода дискретизации T непрерывного сигнала x(t), то устанавливается однозначная связь между этим сигналом и числовой последовательностью. При этом каждое число последовательности x(k) равно значе-
нию непрерывного сигнала в момент времени t=kT: |
|
x(t)=x(kT). |
(4) |
Это равенство показывает, что одной и той же последовательности x(k) соответствуют различные непрерывные сигналы, отличающиеся только масштабом по оси времени. Последовательность (3) имеет своим z-преобразованием следующее выражение:
|
|
−1 |
|
−k |
∞ |
−k |
|
|
|
+ x(1)z |
+ x(2)z +......x(k)z |
+.... = ∑ x(k)z |
. |
(5) |
|||||
X(z) = x(0) |
|
|
|
k=0
Это выражение называется прямым z-преобразованием функции дискретного времени или числовой последовательности x(k). Из этого выражения следует, что для того, чтобы заданной функции (последовательности) x(k) поставить в соответствие z-преобразование, необходимо каждый отсчет функции(член последовательности) умножить на некоторую комплексную переменную z-k, где k номер отсчета функции, а затем сложить результаты. При этом каждое произведение, входящее в сумму (5), однозначно соответствует определенному отсчету функции. Показатель степени k говорит о месте коэффициента в последовательности чисел.
Зададим, например, некоторую числовую последовательность x(k)=(0.1; 2.3; 1.05…). Этой последовательности соответствует z – преобразование
X(z) =0.1+2.3z-1+1.05z-2+…..
Произведение 1.05z-2 означает, что в исходной последовательности x(k) число 1.05 идет вторым после начального (нулевого по счету) числа 0.1.
Для сокращения записи в дальнейшем будем употреблять знак соответствия между функцией дискретного времени и ее z-преобразования: x(k) ↔ X(z) .
Z-преобразование позволяет достаточно просто отразить основные операции цифровой обработки сигналов: задержки на определенное число тактов, умножения отсчетов сигнала на весовые коэффициенты и сложения. Так, для единичного импульса, аналогичного δ-функции и имеющего ненулевое значение
только для k=0, прямое z-преобразование X(z) =1. Для единичной ступенчатой
последовательности, принимающей значения, равные единице для всех положительных k, z-преобразование
|
+ z |
−1 |
+ z |
−2 |
+.... = |
∞ |
−k |
, т.е., |
(6) |
X(z) =1 |
|
|
∑ z |
|
k=0
8

является суммой членов геометрической прогрессии.
Использование формул бесконечных рядов дает еще ряд z-преобразований, приведенных в таблице соответствия.
3.Основные свойства прямого z-преобразования.
Вдальнейшем анализе сигналов и дискретных цепей оказываются важными три следующих свойства z-преобразования.
1) Свойство линейности. Если дискретным функциям f(k) и g(k) соответст-
вуют их z-преобразования F(z) иG(z) , то линейной комбинации Af(k)+Bg(k) соответствует линейная комбинация z-преобразований AF(z) + BG(z) .
2) Задержка сигнала на целое число периодов дискретизации. Согласно определению прямого z-преобразования (5) дискретному сигналу f(k), сдвинутому на время m в сторону запаздывания, т.е. сигналу f(k-m) соответствует z – пре-
образование F(z)z −m , где F(z) ↔f(k).
3) Дискретная свертка – эквивалент интеграла наложения для аналоговых цепей. В области оригиналов дискретная свертка записывается так:
k |
|
|
|
y(k) = ∑x(i)g(k −i). |
|
||
i=0 |
|
|
|
|
|
получим z- |
|
Имея z-преобразования X(z) ↔ x(k) |
и G(z) ↔ g(k), |
||
преобразование свертки как произведение z – преобразований: |
|
||
|
|
|
(7) |
Y(z) |
= X(z)G(z) |
||
4. Методы вычисления обратного z – преобразования.
Для нахождения функции дискретного времени x(k) по заданному z- преобразованию X(z) надо вычислить обратное z-преобразование:
x(k) = |
|
1 |
|
|
|
|
|
k−1 |
dz |
|
|
|
|
(8) |
|||||
2πj |
∫X(z)z |
|
|
|
|
|
|||||||||||||
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k−1 |
|
||
Этот интеграл равен сумме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в полюсах внутри |
|||
вычетов функцииX(z)z |
|
||||||||||||||||||
контура C. Если в точке z* функция |
|
|
|
k−1 |
имеет полюс порядка s, , то ее |
||||||||||||||
|
X(z)z |
|
|
|
|||||||||||||||
можно представить так |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k−1 |
= ψ(z) /(z − z* ) |
s |
. |
|
|
|
|||||||||||
X(z)z |
|
|
|
|
|
|
|
||||||||||||
Вычет в точке z* дается формулой |
|
|
|
|
|
|
ds−1 |
|
|
|
|
|
|
|
|||||
|
k−1 |
] = |
|
1 |
|
|
|
|
ψ(z) |
|
. |
|
|||||||
Re s[X(z)z |
|
|
|
|
|
|
|
||||||||||||
|
|
(s −1)! |
dzs−1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z=z* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если в точке z* имется только полюс первого порядка, то |
|
||||||||||||||||||
|
|
|
|
|
|
k−1 |
] |
= ψ(z* ) . |
|
|
|
|
|||||||
Re s[X(z)z |
|
|
|
|
|
||||||||||||||
9
Кроме того, для нахождения функции x(k) по ее заданному z- преобразованию X(z) существует ряд приемов, основанных на свойствах z-
преобразования. Эти приемы можно разделить на две группы: а) аналитические методы отыскания оригиналов x(k).
б) методы численного определения отсчетов функции x(k). 4.1 Использование таблиц z-преобразований.
Этот прием основан на сопоставлении заданных численных коэффициентов перед степенями z-изображения дискретной функции времени и аналогичных коэффициентов в табличных формулах z-преобразований.
Пусть, например, задано z-преобразование сигнала
|
3z |
|
|
X(z) = |
z2 + 0.8 |
. |
(9) |
Требуется найти в аналитическом виде оригинал, соответствующий этому z-преобразованию. Замечая, что высшая степень z в числителе – первая, а знаменателя – вторая и свободный член знаменателя меньше единицы, находим в таблице соответствия дискретных функций и их z – преобразований изображение, соответствующее этим условиям:
|
Aze−αT sin ωT |
|
|
X(z) = |
|
. |
(10) |
z2 − 2e−αT z cos ωT + e−2αT |
|||
Такому изображению соответствует оригинал |
|
||
|
x(kT) = Ae−kαT sin(kωT) . |
(11) |
|
Сопоставляя коэффициенты перед первой степенью z в (9) и (10), а также свободные члены, получим
0 = 2e−αT cos ωT
3 = Ae−αT sin ωT |
(12) |
0.8 = e−2αT
Решение полученной системы уравнений относительно параметров A, α, ω позволяет аналитически определить искомый дискретный сигнал.
Так, из третьего уравнения системы (12) получаем e-αT=(0.8)1/2=0.895.
Отсюда αT=-ln(0.895)=0.11. Подставляя e-αT=0.895 в первое уравнение, по-
лучаем 0=2 0,895cosωT, что дает ωT=π/2+m π (m=0,1….).
Используя второе уравнение, получаем m=0, поскольку A>0 и sinωT>0. Отсюда ω=π/2T. Так как частота дискретизации ωд=2π/T, то частота гармонического сигнала оказывается в 4 раза меньше частоты дискретизации.
Учитывая, что sinωT=1, определяем амплитуду сигнала
A=3/e-αT=3/0.895=3.35.
Таким образом, для заданного z-преобразования (9) дискретный сигнал имеет вид:
x(k)=3.35e-0.11ksin(kπ/2)=3.35 (0.895)k sin(kπ/2).
10
