1. Неопределенность вида .

Теорема 1. Пусть: 1) функции f(x) и g(x) определены в промежутке [a;b],

2) =0.

3) существуют конечные производные и в (a;b), причем ≠0 .

Тогда если существует конечный или бесконечный (определенного знака) предел , то к тому же пределу при ха стремится и отношение , т.е.

(*)

Доказательство.

Т.к. существуют конечные производные функций в точке а, то функции непрерывны в этой точке, и, в силу условия 2), =f(a)=0 и =g(a)=0,

Возьмем на отрезке [a;b] какую-нибудь точку х≠а. Тогда, по теореме Коши,

Где с лежит между а и х (а<c<х). Т.к. =f(a)=0 и =g(a)=0, то



Перейдем в последнем равенстве к пределу при ха, получим

По условию существует. Тогда существует и

и = ч.т.д.

Примеры.

1)

2)

Замечание 1. Если отношение производных опять приводит к неопределенности вида , но к отношению производных можно применить установленное правило, то переходят к отношению вторых производных. Если и после этого получается неопределенность вида , то переходят к отношению 3-х производных и.т.д. Если на каком-то шаге получается предел, который можно вычислить, то найденное значение и будет искомым пределом отношения функций.

Пример.

, , значит

Замечание 2. Если не существует предел отношения производных, то это не означает, что не существует предел отношения самих функций.

Пример.

Не существует , т.к. не существует , но

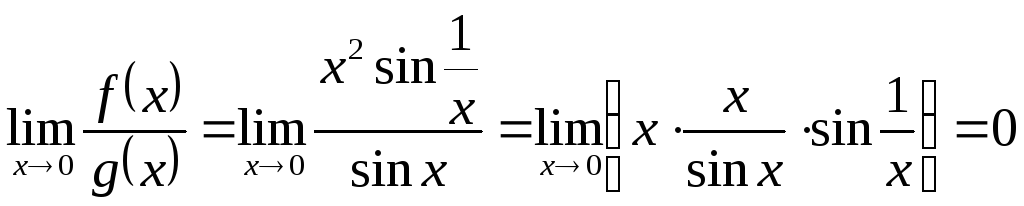, т.к. , а функция - ограниченная.

Правило Лопиталя применимо и в том случае, если =0.

Теорема 2. Пусть: 1) функции f(x) и g(x) определены на промежутке (b,+),

2) =0.

3) существуют конечные производные и на (b,+), причем ≠0 .

Тогда если существует конечный или бесконечный (определенного знака) предел , то к тому же пределу при х+ стремится и отношение , т.е.

(*)

Доказательство. Сделаем замену переменной: х= (t=). Тогда

1) t+0, при x+; 2) функции φ(t)= и ψ(t)= определены на промежутке , 3) на промежутке существуют конечные производные , , причем для t; 4) ,

Т.о. функции φ(t) и ψ(t) на промежутке удовлетворяют условиям теоремы 1.

По теореме 1: , но

Поэтому ч.т.д.

Замечание. Эта теорема остается верной с соответствующими видоизменениями и при х-.

Пример.

2. Неопределенность вида .

Теорема 3. (б/д) Пусть: 1) функции f(x) и g(x) определены в промежутке (a;b) (а - конечное число, a<b) ,

2) =.

3) существуют конечные производные и в (a;b), причем ≠0 .

Тогда если существует конечный или бесконечный (определенного знака) предел , то к тому же пределу при ха стремится и отношение , т.е.

(*)

Пример. 1)

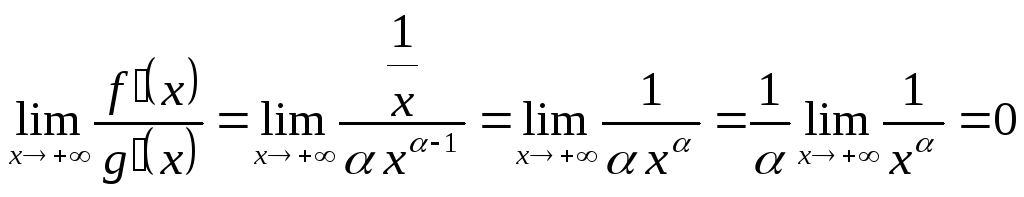. Значит, и

Вывод. При х+ функция f(x)=ln x растет медленнее, чем любая положительная степень переменной х.

2)

Замечание 1. Если отношение производных опять приводит к неопределенности вида , но к отношению производных можно применить установленное правило, то переходят к отношению вторых производных. Если и после этого получается неопределенность вида , то переходят к отношению 3-х производных и.т.д. Если на каком-то шаге получается предел, который можно вычислить, то найденное значение и будет искомым пределом отношения функций.

Пример. , где nN, a>1.

. Если n>1, то при х+ представляет неопределенность вида . Поэтому переходим к нахождению предела отношения вторых производных и т.д. На n-м шаге получим:

. Значит и =0.

Вывод. При х+ функция f(x)=хⁿ, nN растет медленнее, чем показательная функция а^х (а>1).